 |
Перемножение эпюр произведем по правилу Верещагина и правилу Симпсона.
|
|
|
|
EJ 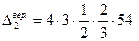 (по Верещагину)
(по Верещагину)  (по Симпсону)
(по Симпсону)  .
.
Точка 2 перемещается вниз на 504 единицы.
Задача 2. Определить угол поворота сечения 4.
Прикладываем сосредоточенный изгибающий момент М = 1 к сечению 4 (рис. 46г) и строим от него эпюру М1. Перемножаем полученную эпюру М1 на Мр (она остается прежней – рис. 46б).
EJ  (единиц – радиан).
(единиц – радиан).
Задача 3. Определить взаимное смещение узлов 1 и 2.
Прикладываем к точкам 1 и 2 две единичные противоположно направленные силы, линия действия которых проходит по линии 1 – 2 (рис. 46д). Строим от обобщенной единичной нагрузки эпюру М1 (рис. 46е).
Перемножение эпюр М1 и Мр дает:
 .
.
Пример 3.
Ферма (рис. 47а) загружена системой сил. Требуется определить вертикальное перемещение узла 3 - 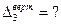
Определяем усилия в стержнях фермы от внешнего и единичного (рис. 47а,в) загружений. Результаты сведем в таблицу 3.
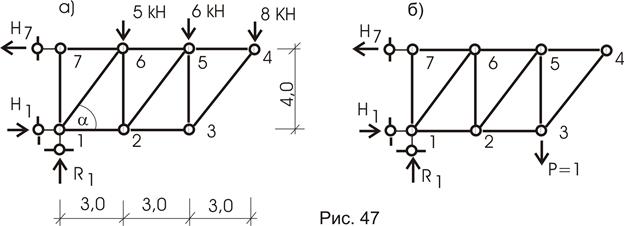
Таблица 3
| № стержня | 1-2 | 2-3 | 3-4 | 5-3 | 5-2 | 2-6 | 6-1 | 1-7 | 7-6 | 6-5 | 5-4 |
| Длина | 3.0 | 3.0 | 5.0 | 4.0 | 5.0 | 4.0 | 5.0 | 4.0 | 3.0 | 3.0 | 3.0 |
| Усил. Р | -16.5 | -6.0 | -10.0 | 8.0 | -17.5 | 14.0 | -23.75 | 30.75 | 16.5 | 6.0 | |
| Усил. 1 | -0.75 | 1.0 | -1.25 | -1.25 | 1.5 | 0.75 |
 ;
;  .
.
EJ 
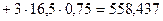 .
.
Результат есть сумма произведений усилий Np на N1 и на длину стержня, соответственно.
Пример 4.
Дана рама (рис. 48а), загруженная единичной силой Р = 1кн. Необходимо определить величину перемещения точки приложения этой силы по ее направлению. Эпюра Мp от внешнего загружения показана на рисунке 48б.
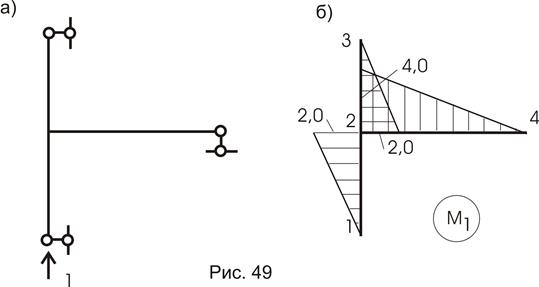
Загружаем раму единичной нагрузкой Р = 1, приложенной к точке 1 (к точке приложения внешней нагрузки) по направлению силы Р = 1 (кн) – рис. 49а, и строим эпюру М1 (рис.49б). Сравнивая эти две эпюры, видим, что они равны во всех отношениях, а это означает, что формулу Мора можем записать:
 .
.
В этом случае мы говорим, что эпюру перемножаем саму на себя.
|
|
|
Читатель, отметьте это для себя - этим мы в дальнейшем будем пользоваться неоднократно.
EJ  .
.

Пример 5.
Рама (рис.50а). Опора 4 просела на величину  . Определим горизонтальное перемещение узла 2. К узлу 2 приложим горизонтальную силу Р=1 (рис.50б) и определим от этого загружения реакцию четвертой опоры:
. Определим горизонтальное перемещение узла 2. К узлу 2 приложим горизонтальную силу Р=1 (рис.50б) и определим от этого загружения реакцию четвертой опоры:

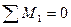 ;
;  , откуда
, откуда  .
.
Используя четвертое слагаемое формулы Мора, определим:
 .
.
Знак минус в скобках взят потому, что направления реакции  и перемещения опоры различные.
и перемещения опоры различные.
Пример 6.
На конструкцию (рис. 51а) воздействует температура. Определим перемещение узла 3 по горизонтали. В решении этой задачи участвуют пятое

и шестое слагаемые формулы Мора. Необходимо отметить, что оба слагаемые равноправны. Приложим к узлу 3 единичную силу (рис. 51б). Построим эпюры моментов и продольных усилий (рис. 51в,г). Перед вычислением искомого перемещения отметим правила знаков:
- для изгибающего момента:
если воздействие температуры и единичная сила растягивают волокна стержня с одной стороны относительно оси, то знак вычисления положительный;
- для продольного усилия:
если температура и единичная сила вызывают деформацию стержня одного направления, то знак вычисления положительный.
Вычислим искомое перемещение:

Глава 2. Статически неопределимые конструкции
2.1 Расчет конструкций методом сил
Пример 1. Требуется рассчитать конструкцию (рис. 52).
Решение.
- Определение степени свободы конструкции
 .
.
Это говорит о наличии 2-х избыточных связей.
- Основная система для расчета получается удалением 2-х связей. Необходимо помнить о безусловно необходимых связях (их нельзя удалять) и условно необходимых, которые можно удалить.
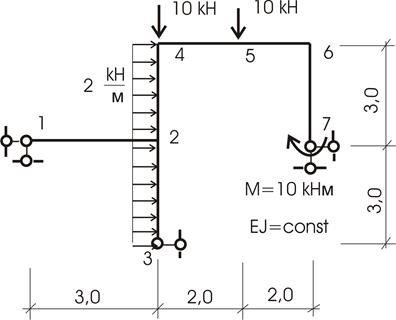
Рис. 52
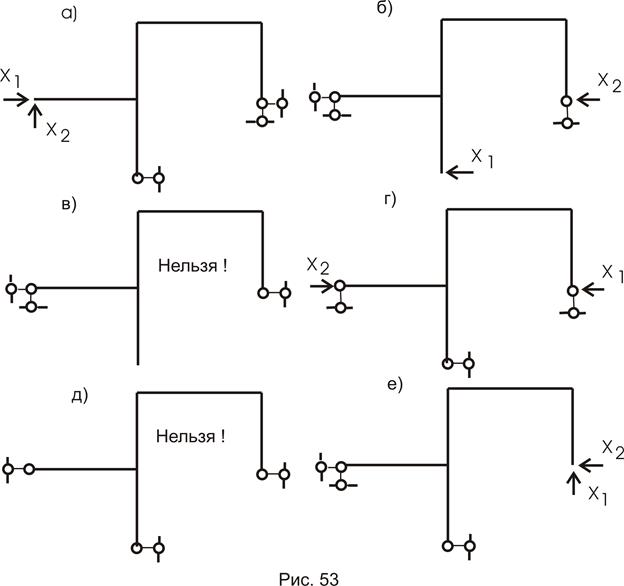
Варианты основной системы приведены на рисунке 53. Варианты в) и д) использовать в дальнейших расчетах, как уже написано, нельзя, т. к. удалены безусловно необходимые связи и получаемая основная система мгновенно изменяемая!
|
|
|
Привычна по виду схема б), но оптимальной для дальнейшего расчета будет схема г). Примем ее за основную систему.
- Для основной системы запишем уравнения совместности деформации или канонические уравнения:
 ;
;
 .
.
Каждое из этих уравнений гласит: суммарное перемещение точки приложения неизвестных усилий по их направлению от воздействия всех сил, действующих на конструкцию, равно нулю.
Здесь  - перемещение точки приложения i -ой неизвестной по ее направлению от воздействия к-ой силы
- перемещение точки приложения i -ой неизвестной по ее направлению от воздействия к-ой силы  ;
;
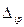 - перемещение точки приложения i -ой силы по ее направлению от воздействия на конструкцию внешней нагрузки.
- перемещение точки приложения i -ой силы по ее направлению от воздействия на конструкцию внешней нагрузки.
Для определения этих коэффициентов и грузовых слагаемых строим эпюры изгибающих моментов от сил  и от внешней нагрузки (рис. 54).
и от внешней нагрузки (рис. 54).
Вычисляем 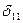 :
:
 .
.
Эпюру М1 перемножаем саму на себя:
 .
.
Вычисляем  .(Перемножаются эпюры М1 и М2 ):
.(Перемножаются эпюры М1 и М2 ):

 .
.
Вычисляем  . (Перемножается эпюра М2 сама на себя):
. (Перемножается эпюра М2 сама на себя):

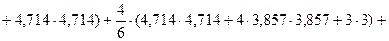
 .
.
Вычисляем  . (Перемножаются эпюры М1 на МР ):
. (Перемножаются эпюры М1 на МР ):

Рис. 54


 .
.
Вычисляем  . (Перемножаются эпюры М2 на МР):
. (Перемножаются эпюры М2 на МР):
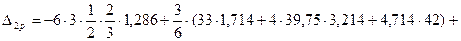
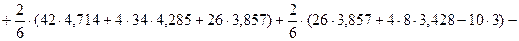
 .
.
- Решение системы:
 х1= - 12,155 кн;
х1= - 12,155 кн;
 х2= - 2,368 кн.
х2= - 2,368 кн.
- Построение эпюр внутренних усилий для заданной рамы.
1-ый путь построения
К основной системе (рис. 55) приложим заданную нагрузку и найденные усилия в отброшенных связях с учетом их знака. Для полученной схемы строим эпюры внутренних усилий обычным путем (методами сопротивления материалов).

Определяем реакции в связях:
 ;
; 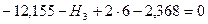 .
.
 кн.
кн.
 ;
;  .
.
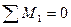 ;
;  .
.
 .
.
 (кн).
(кн).
Тогда из второго уравнения  кн.
кн.
Эпюры внутренних усилий М, Q и N показаны на рисунке 56(а,б,в). Читателю предлагается самостоятельно построить их и результаты сравнить.
- Производим статическую проверку – равновесие узла должно сохраняться (рис. 56г,д).
 ;
;  ,
,  .
.
 ;
;  ,
,  .
.
 ;
; 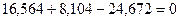 ,
,  .
.

- Кинематическая проверка.
 ,
,
где 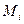 - одна из единичных эпюр
- одна из единичных эпюр 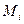 .
.
Перемножим  (рис.56а) на
(рис.56а) на 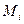 (рис. 54а):
(рис. 54а):
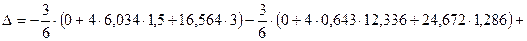


Процент погрешности составит:
 .
.
2-ой путь построения
Он основан на принципе независимости действия сил (рис. 57).
 .
.

Сравнивая полученные результаты, по  мы видим небольшие погрешности вычисления. Следуя дальше вторым путем, эпюру Q оk строим по эпюре Мок. Для этого нашу раму расчленим на отдельные элементы (балки): 1 – 2; 2 – 3; 2 – 4; 4 – 6; 6 – 7, т. е. на 5 отдельных балок (рис.58). Загружаем их внешней нагрузкой и моментами в жестких узлах, взятых из эпюры Мок (рис.57).
мы видим небольшие погрешности вычисления. Следуя дальше вторым путем, эпюру Q оk строим по эпюре Мок. Для этого нашу раму расчленим на отдельные элементы (балки): 1 – 2; 2 – 3; 2 – 4; 4 – 6; 6 – 7, т. е. на 5 отдельных балок (рис.58). Загружаем их внешней нагрузкой и моментами в жестких узлах, взятых из эпюры Мок (рис.57).
|
|
|
Разберем одну из балок, скажем, балку 2 – 4 (рис. 58в). Для удобства расположим ее горизонтально (рис. 58е).
Определяем опорные реакции
 ;
;  .
. 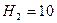 кН.
кН.
 ;
;  .
.
 ;
;  .
.
 (кН).
(кН).
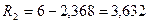 (кН).
(кН).
По этим данным строим эпюру Q (рис. 58е).

Сравнивая значения и знаки (!) с эпюрой Q ok, построенной ранее
(рис. 52), на этом участке мы видим полное совпадение.
Эпюру N ok строим по эпюре Q ok, используя способ вырезания узлов, как это делалось в статической проверке, где мы показали это на примере одного узла. Используя результаты Qок, построенной ранее, покажем на примере узла 4 определение продольных усилий в стержнях 4 – 2 и 4 – 6 (рис. 59).
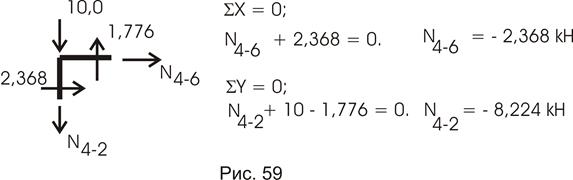
Cверим значения  и
и  со значениями, найденными ранее (рис. 56) – они полностью совпадают.
со значениями, найденными ранее (рис. 56) – они полностью совпадают.
Приведем пример расчета рамы без пояснений (рис. 60).

1.  .
.
2. На рисунке 61 приведены варианты основных систем.
Делаем выбор на варианте а).

3. 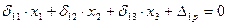 ;
;
 ;
;
 .
.


 ;
;
 ;
;
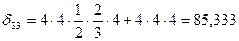 ;
;
 ;
;
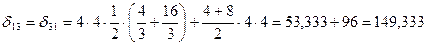 ;
;
 ;
;


 ;
;

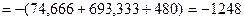 ;
;
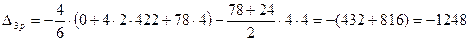 .
.
Проверили? Все правильно?
Система уравнений:
 ;
;
 ;
;
 .
.

Получаем:  кН;
кН; 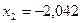 кН;
кН;  кН.
кН.
Загружаем конструкцию найденными усилиями и внешней нагрузкой (рис. 63). Окончательные эпюры внутренних усилий приведены на рисунке 64.

Статическая проверка.
По моментам видно (из эпюры М – рис. 64 -все узлы в равновесии. По Q и N рассмотрим характерные узлы (рис. 65а,б). Видим, что уравнения статики соблюдаются.
Кинематическая проверка.

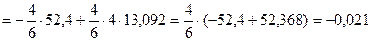 .
.

Погрешность составляет 0,04%.
Пример расчета статически неопределимой балки
Для балки (рис. 66а) определим внутренние усилия.

Решение.
1)  .
.
Два раза статически неопределимая балка. Основные системы метода сил представлены на рисунке 66 б,в.
Для расчета примем вариант в).
2) Запишем систему канонических уравнений:
 ;
;
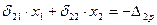 .
.
3) Вычисляем коэффициенты  и
и  .
.
Эпюры от единичных загружений представлены на рисунке 67б,в) и от внешней нагрузки - на рисунке 67г.
|
|
|

 ;
;  ;
;
 ;
;
 ;
;  .
.
Решение системы:
 ;
;
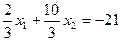 .
.
Дает 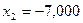 кнм;
кнм; 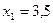 кнм.
кнм.
По полученным значениям строим  и
и 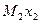 (рис. 68а,б)
(рис. 68а,б)
и  (рис. 68в).
(рис. 68в).
Проверки.
а) Статическая проверка. Значения моментов на опорах (рис. 68в) одинаковы и равновесие обеспечивается. Проверка удовлетворяется.
б) Кинематическая проверка.

Перемножим  с
с  . Проверим, будет ли взаимный угол поворота сечений балки на опоре 2 равен нулю?
. Проверим, будет ли взаимный угол поворота сечений балки на опоре 2 равен нулю?
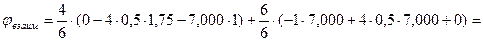
 . Проверка удовлетворяется.
. Проверка удовлетворяется.
Эпюра  строится по эпюре
строится по эпюре  по рассмотренному ранее принципу. Выполните построение самостоятельно и свой результат сверьте с приведенным решением на рисунке 68г.
по рассмотренному ранее принципу. Выполните построение самостоятельно и свой результат сверьте с приведенным решением на рисунке 68г.
2.2 Расчет неразрезных балок
Для балок с большим числом пролетов (неразрезные балки – рис. 69а) оптимальная основная система получается введением шарниров во все опорные узлы (как это мы сделали для разобранной выше балки – рис. 66в). На полученной основной системе (рис. 69б) направление неизвестных моментов показаны на трех опорах, входящих в общее уравнение.
Для неразрезных балок неизвестные обозначаются через 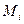 - изгибающий момент на
- изгибающий момент на  ой опоре. Опуская доказательства, распишем одно уравнение из системы канонических уравнений для основной системы (рис. 69б), скажем, для
ой опоре. Опуская доказательства, распишем одно уравнение из системы канонических уравнений для основной системы (рис. 69б), скажем, для  - ой опоры при
- ой опоры при  :
:
 .
.
Данное уравнение носит название - уравнение трех моментов.
В этом уравнении:  - длина пролета (пролет нумеруется по номеру правой опоры);
- длина пролета (пролет нумеруется по номеру правой опоры); 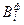 и
и  - фиктивные реакции (
- фиктивные реакции (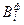 - правая реакция для
- правая реакция для  - го пролета;
- го пролета;  - левая реакция для
- левая реакция для 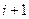 пролета). Они получаются от нагрузки, представленной эпюрой моментов соответствующих пролетов, которые, в свою очередь, строятся от заданного загружения соответствующих пролетов.
пролета). Они получаются от нагрузки, представленной эпюрой моментов соответствующих пролетов, которые, в свою очередь, строятся от заданного загружения соответствующих пролетов.
Тогда левая часть системы канонических уравнений будет представлять собой ленточную матрицу вида (для шести неизвестных):

Рис. 69
 .
.
Заметим, что уравнения (за исключением первого и последнего) содержат только три слагаемых.
Вернемся к балке, представленной на рисунке 66а.
Для получения основной системы примем следующие упрощения:
- заделку заменим фиктивным пролетом, равным нулю;
- консоль отбросим, но влияние нагрузки на консоли выразим (заменим) через опорный момент  и примем его со знаком минус, т. к. данный момент растягивает верхние волокна, а неизвестные опорные моменты, как видно из основной системы, - нижние (рис. 70а).
и примем его со знаком минус, т. к. данный момент растягивает верхние волокна, а неизвестные опорные моменты, как видно из основной системы, - нижние (рис. 70а).

Запишем уравнения трех моментов для каждого неизвестного момента. Для опоры 1:
 .
.
Для опоры 2:

Упростим левую часть уравнений, зная, что 
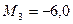 и величину пролетов:
и величину пролетов:
 ;
;
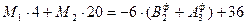 .
.
Для определения 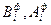 загрузим основную систему внешней нагрузкой (рис70б). Загружен третий пролет равномерно распределенной нагрузкой, от которой эпюра моментов представляет собой квадратную параболу с ординатой по середине
загрузим основную систему внешней нагрузкой (рис70б). Загружен третий пролет равномерно распределенной нагрузкой, от которой эпюра моментов представляет собой квадратную параболу с ординатой по середине
|
|
|
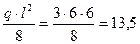 (кнм).
(кнм).
Эту эпюру моментов представляем в виде фиктивной нагрузки на третьем пролете (рис. 70в). От этой нагрузки вычисляем фиктивные опорные реакции:
 (кнм2).
(кнм2).
Учитывалась симметричность загружения (получаем величину реакций, как половину площади квадратной параболы).
На пролетах 1 и 2 нет нагрузки и поэтому  .
.
Вычисляем и правую часть уравнений:
 ;
;

или
 ;
;
 .
.
Из первого уравнения находим:
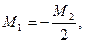
тогда из второго определим:
 и
и  .
.
Сравнивая результаты с вычисленными обычным путем (рис.68в), видим их совпадение.
Рассмотрим следующий пример (рис. 71а).
1. Выбираем основную систему (рис. 71б).
2. Записываем уравнения 3-х моментов:
 ;
;
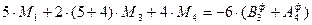 ;
;
 .
.

Для вычисления 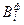 и
и  построим эпюры изгибающих моментов в основной системе от внешней нагрузки (рис. 71в,г).
построим эпюры изгибающих моментов в основной системе от внешней нагрузки (рис. 71в,г).
3. Вычисляем фиктивные реакции:
Второй пролет:
 .
.  .
.
Третий пролет:
 ;
;  .
.
Четвертый пролет:
 ;
; 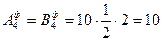 .
.
Подставим полученные значения в уравнения:


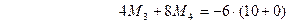 .
.
4. Решение системы дает:
 .
.
5. Построение окончательных эпюр.
Эпюра изгибающих моментов.
В неразрезных балках окончательная эпюра  (рис. 71е) строится путем сложения эпюры
(рис. 71е) строится путем сложения эпюры  (рис. 71г) и эпюры опорных моментов (рис. 71д).
(рис. 71г) и эпюры опорных моментов (рис. 71д).
Эпюра Qок строится уже известными приемами (рис. 71ж):
для балки 1 – 2:
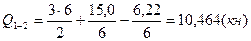 ;
;  (кн);
(кн);
для балки 2 – 3:
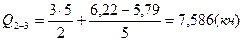 ;
;  (кн);
(кн);
для балки 3 – 4
 ;
; 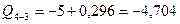 (кн).
(кн).
Опорные реакции определяются по эпюре  . Можно использовать два подхода:
. Можно использовать два подхода:
1) Используем правило – в точке приложения сосредоточенной силы на эпюре  наблюдается скачок на величину данной силы. Отсюда:
наблюдается скачок на величину данной силы. Отсюда:


2) Равновесие опорного узла.

Вырезаем опорный узел (для примера – узел 2, рис. 72). В местах разреза появляются перерезывающие силы, их направляем с учетом знака. Тогда:
 дает:
дает: 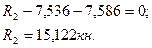
|
|
|


