 |
Расчет конструкций методом перемещений
|
|
|
|
В качестве неизвестных принимаются перемещения узлов конструкции. Каждый узел в общем случае имеет три возможных перемещения: линейное перемещение по горизонтали; линейное перемещение по вертикали; угловое перемещение (угол поворота) жесткого соединения стержней в узле.

Общий подсчет неизвестных ведется по формуле:


где z – общее количество неизвестных перемещений; zугл . – угловые перемещения жестких узлов конструкций; zлин . – линейные независимые перемещения всех узлов конструкции.
Если zугл . всегда равно количеству жестких узлов конструкции (на рисунке 73а один жесткий узел 1), то zлин . равно степени свободы шарнирной схемы конструкции (рамы).
Для получения шарнирной схемы рамы вводятся шарниры во все жесткие узлы рамы, включая и жесткие заделки (опоры) (рис. 73б). Для полученной рамы подсчитываем степень свободы:
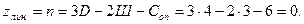
Результат еще не означает, что zлин. = 0. Необходимо провести анализ полученной конструкции. Заметим, что шарниры 0, 1, 4 лежат на одной прямой, что означает – система мгновенно изменяемая, узел 2 при этом не ликвидирует этого дефекта. Нам необходимо поставить опорный стержень по горизонтали в узел 1 или в узел 2 и тогда:

Основная система метода перемещений - единственная. Она получается путем закрепления всех возможных перемещений узлов рамы (конструкции)
введением в жесткие узлы заделки (заделки препятствуют только повороту узла) и опорных стержней по возможным перемещениям узлов шарнирной схемы конструкции.

Для приведенной рамы (рис. 73) основная система показана на рис. 74. Общее число неизвестных будет равно 2 – по количеству введенных связей.

Для рамы (рис. 75) основная система приведена на рис.76. Здесь установлено три жесткие связи и две линейные в виде опорных стержней. И мы получили:
|
|
|

Количество введенных связей в конструкцию (раму) определяет и степень кинематической неопределимости рамы. В первом примере она равна 2, во втором – 5. В каждой введенной связи возникают реактивные усилия: в заделке - только момент (заделка не препятствует линейному смещению!), а в линейных связях - только реакция (усилие) по направлению этой связи.
Приведение основной системы к исходной производится условием:
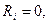
т. е. реактивное усилие в i -ой связи равно нулю, т. к. в заданной системе этой связи нет.
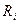 по принципу независимости действия сил (воздействий) запишется:
по принципу независимости действия сил (воздействий) запишется:
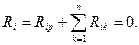
Распишем это условие для первой приведенной конструкции (рис. 74):
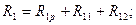

Для второй конструкции (рис. 76) мы получим уже 5 уравнений по числу неизвестных перемещений. Вот одно из них (для третьей связи):

Здесь 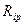 - реактивное усилие в i -ой связи от внешней нагрузки;
- реактивное усилие в i -ой связи от внешней нагрузки;  - реактивное усилие в i -ой связи от перемещения к -ой связи.
- реактивное усилие в i -ой связи от перемещения к -ой связи.
Реакция  с перемещением связана соотношением:
с перемещением связана соотношением:

где  - реактивное усилие в i -ой связи от перемещения к -ой связи на единицу;
- реактивное усилие в i -ой связи от перемещения к -ой связи на единицу;  - истинное перемещение к -ой связи.
- истинное перемещение к -ой связи.
Подставляя последнее соотношение в условия  , получаем систему канонических уравнений. Для первой конструкции (рис. 74) она запишется:
, получаем систему канонических уравнений. Для первой конструкции (рис. 74) она запишется:



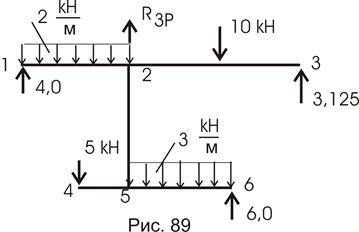
Рассчитаем раму, представленную на рисунке 77.

Число неизвестных:
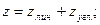
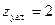 (два жестких узла).
(два жестких узла).
Линейные неизвестные определяются из шарнирной схемы рамы (рис. 78а):
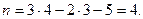
Узлы 1, 2, 3 находятся на одной прямой и, если не установим недостающую связь в узел 2 по вертикали, получим мгновенно-изменяемую конструкцию. Поэтому установим в узел 2 по вертикали недостающую связь. Основная системе показана на рис. 78б (нумерация связей в кружочках) 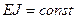 .
.
Система канонических уравнений запишется:
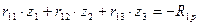 ;
;
 ;
;

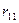 - реактивное усилие в первой связи от перемещения первой связи на единицу. Первая связь заделка. Значит она может поворачиваться. Даем ей поворот на
- реактивное усилие в первой связи от перемещения первой связи на единицу. Первая связь заделка. Значит она может поворачиваться. Даем ей поворот на 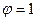 . Произойдет деформация только тех стержней, которые составляют этот узел (рис. 78в). По деформированному состоянию строим
. Произойдет деформация только тех стержней, которые составляют этот узел (рис. 78в). По деформированному состоянию строим
|
|
|

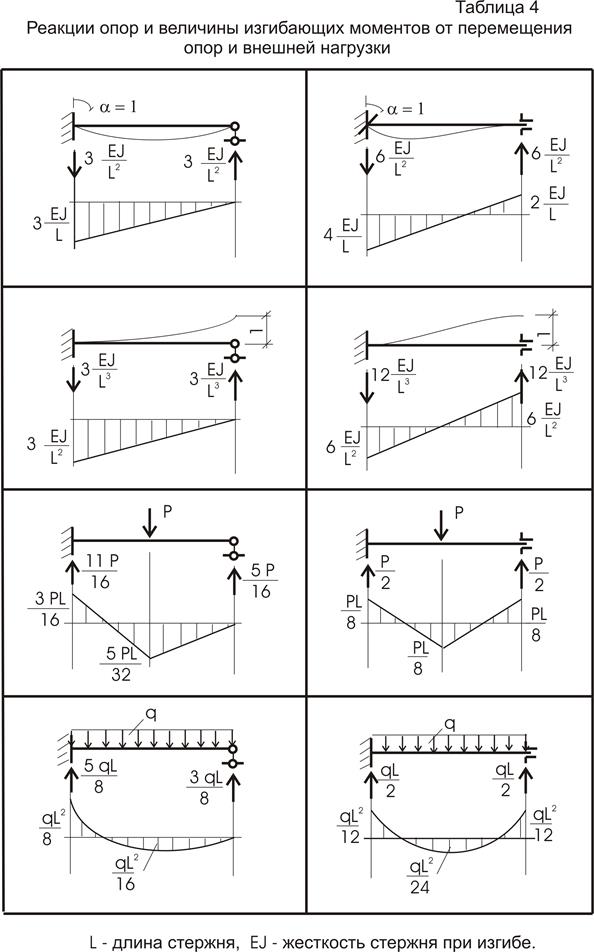
эпюры изгибающих моментов (рис. 78г), используя уже готовые решения (таблица 4). Вырезая узел со связью 1 (рис. 81), найдем 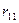 . Направление
. Направление 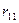 считаем положительным, если оно направлено по направлению перемещения связи:
считаем положительным, если оно направлено по направлению перемещения связи:
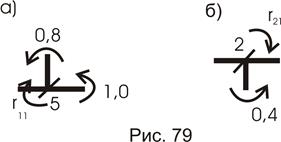
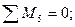
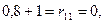
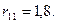
Перемещение связи 1 вызывает реакции во введенных связях 2 и 3. Вырезаем узел со второй связью (рис. 79б) и найдем  :
:

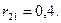
Для получения величины в третьей связи проводим сквозное сечение. Оно пройдет по связи 3, по опоре 1, 6, далее по опоре 3 (рис.80). Реакции в опорах 1, 3 равны нулю, а реакция в опоре 6 равна  (по табличным данным). Знак или направление
(по табличным данным). Знак или направление 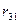 будет зависеть от направления перемещения третьей связи. Не будем торопиться с этим.
будет зависеть от направления перемещения третьей связи. Не будем торопиться с этим.

Дадим перемещение второй связи – угол поворота узла 2 по часовой стрелке (рис. 81), т. е. перейдем к определению величины  и производных от этого перемещения. Деформируются стержни, сходящиеся в узел 2 (рис.81). По табличным решениям строим эпюру М2 (рис. 82а).
и производных от этого перемещения. Деформируются стержни, сходящиеся в узел 2 (рис.81). По табличным решениям строим эпюру М2 (рис. 82а).
Вырезая узел со связью 2, из его равновесия найдем  (рис.82б).
(рис.82б).
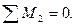
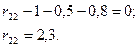
Вырезая узел 5 со связью 1, определим 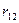 , но
, но  , а мы
, а мы  уже определили
уже определили  .
.
 Читатель может еще раз проверить наши рассуждения. Мы не будем
Читатель может еще раз проверить наши рассуждения. Мы не будем
торопиться с определением 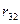 .
.
Даем перемещение третьей связи на единицу (рис. 83). Теперь самое время вернуться к определению 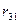 (рис. 80). Возьмем перемещение третьей связи вверх (как направили
(рис. 80). Возьмем перемещение третьей связи вверх (как направили 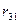 на рис.80, но это совсем необязательно).Для деформированных стержней (рис.83) строим эпюры М, используя таблицу (рис. 81). Теперь проецируя на ось у усилия 0,375 и
на рис.80, но это совсем необязательно).Для деформированных стержней (рис.83) строим эпюры М, используя таблицу (рис. 81). Теперь проецируя на ось у усилия 0,375 и 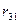 из рисунка 80, находим:
из рисунка 80, находим:
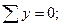

Проверим. Вырежем из М3 узел 5 с первой связью (рис. 85а):
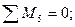

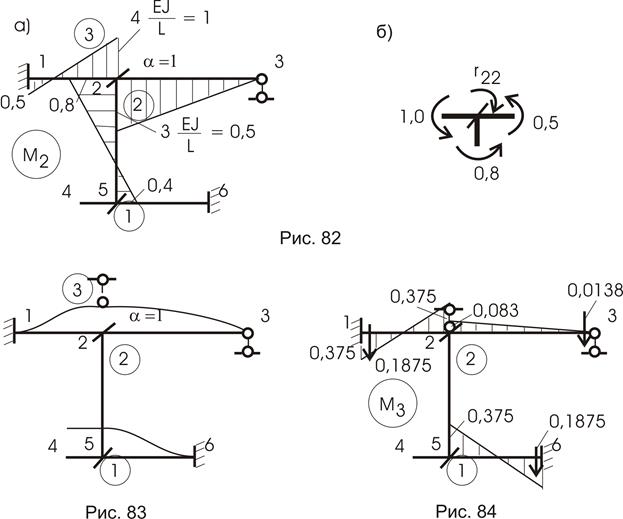
Видим полное совпадение 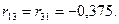
Вырезая узел 2 со второй связью, найдем  и
и 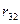 (рис. 85б):
(рис. 85б):



Для определения 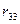 проведем сечение по связи третьей и по опорам 1, 6, 3, получим (рис. 86):
проведем сечение по связи третьей и по опорам 1, 6, 3, получим (рис. 86):

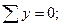
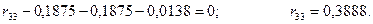
Коэффициенты при  вычислили.
вычислили.
Перейдем к определению 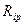 . Для этого построим эпюру Мр (рис. 87) от внешнего загружения по табличным решениям.
. Для этого построим эпюру Мр (рис. 87) от внешнего загружения по табличным решениям.
Определяем  . Вырезаем узел 5, рис. 88а:
. Вырезаем узел 5, рис. 88а:
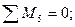


Определяем  . Вырезаем узел 2, рис. 88б:
. Вырезаем узел 2, рис. 88б:
|
|
|

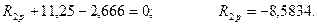
Определяем  (рис. 92):
(рис. 92):
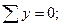
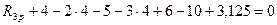 ,
,
откуда 
Система канонических уравнений готова к решению:
 ;
;
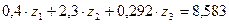 ;
;

Из решения системы получаем:
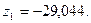
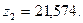

Для построения окончательных эпюр M, Q, N воспользуемся вторым путем, как при методе сил, а именно:

Процесс построения эпюры Мок можно проследить по рисунку 90. Производим проверки правильности построения эпюры Мок:
1. Статическая (вырезаются узлы 2 и 4 – рис. 91):

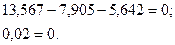
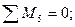

Грубоватый расчет.
2. Кинематическая.
Для кинематической проверки необходимо построить эпюру М1 для точки, заведомо зная ее перемещение. Лучше всего построить М1 метода сил. Самое простое: выберем основную систему метода сил, оставив опору 1(заделку). Приложим к точке 3 по вертикали единичную силу и построим эпюру М1 (рис. 92):

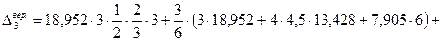
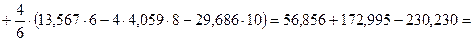

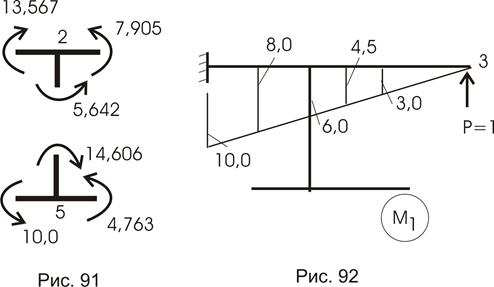
Что составляет погрешность счета: 
Не так уж и плохо!
Проверки дают нам основание построить Qок по Мок уже разобранными нами приемами. Процесс построения эпюры Qок можно проследить по рисункам 93, 94, где рассмотрены отдельные балки, выделенные из рассчитываемой рамы (консоль не приводится – эпюра Q для нее строится обычным порядком).
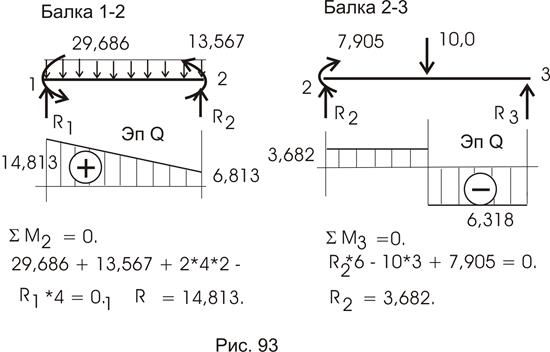
В окончательном виде эпюра перерезывающих сил приведена на рисунке 96.
Эпюру Nок строим по эпюре Qок.
Рассматриваем равновесие узла 5 (рис. 96), что позволяет определить продольные усилия в стержнях 5-6 и 5-2. Рассмотрим и равновесие узла 2 (рис. 97), из рассмотрения которого определяются усилия в стержнях 1-2 и

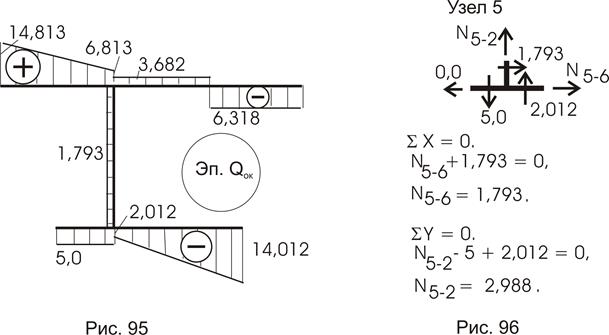
5-2. Следует отметить, что полученные значения продольного усилия в стержне 5-2 при рассмотрении узлов 5 и 2 имеют расхождения в 0,131 (кН). Это нужно отнести на ошибки в наших расчетах.
Окончательная эпюра продольных усилий показана на рисунке 98.

Рассмотрим еще пример.
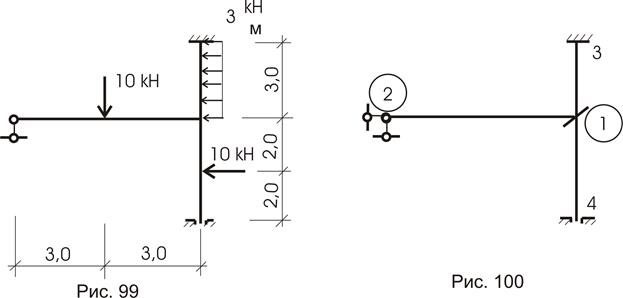
Требуется для конструкции (рис. 99) определить внутренние усилия (построить эпюры M, Q, N).
Расчет произведем двумя методами:
методом перемещений и методом сил (для сравнения).
Расчет рамы методом перемещений
а) Основная система показана на рисунке 100. Одно угловое неизвестное и одно линейное.
|
|
|
б) Канонические уравнения:


Для вычисления  и
и 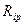 построим эпюры моментов от перемещений связей
построим эпюры моментов от перемещений связей 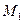 (рис. 101) и
(рис. 101) и  (рис. 102). Вырезая узел со связью 1 из М1 и рассмотрев его равновесие, получим:
(рис. 102). Вырезая узел со связью 1 из М1 и рассмотрев его равновесие, получим:
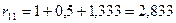 .
.

Проведя сечение по опорам из М2, найдем:
 .
.
Вырежем узел со связью 1 из М2, определим
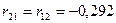 .
.
Эпюра Мр приведена на рисунке 103. Вырезание узла со связью 1 (рис. 104) позволяет вычислить 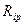 :
:


Сечение второй связи и опор рамы дает  :
:


в) Решение системы дает величину перемещений наложенных связей:
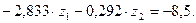
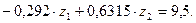
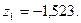
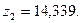
г) Эпюру Мок построим по принципу:

Эпюры  и
и  представлены на рисунке 105а,б.
представлены на рисунке 105а,б.


Рис. 106
|
|
|


