Главная | Обратная связь | Поможем написать вашу работу!

Правило сложения дисперсий

Если совокупность состоит из нескольких частей, то можно определить в пределах каждой не только среднюю величину, но и дисперсию (частную дисперсию). Обозначив через отклонение простой средней от общей, получим:

Правило сложения дисперсий означает, что общая дисперсия складывается из двух слагаемых, одно из которых измеряет вариацию внутри частей совокупности, а второе — различия (вариацию) между этими частями (представленными средними). Именно поэтому правило сложения дисперсий находит широкое применение в анализе взаимосвязей и зависимостей.

Наглядно представить статистические данные позволяет графический метод, заключающийся в изображении показателей при помощи геометрических фигур и т.д. Передаваемая графически информация воспринимается значительно лучше, чем текстовая запись цифровых данных.

Поле графика — это пространство, в котором располагается графический образ.

Рис. 3.2. Полигон распределения семей по числу их членов

Шкалой называется линия, отдельные точки которой могут быть прочитаны как определенные числа.

Масштаб — мера перевода числовой величины в графическую. Масштаб графика выражается линейной мерой, т.е. числом миллиметров в отрезке, которому должна соответствовать единица статистического показателя.

В большинстве случаев в статистических графиках применяется система декартовых координат. Графический образ зависит от используемых геометрических знаков и может быть точечным, круговым, столбиковым и др.

Диаграмма — наиболее распространенная форма графических изображений.

Диаграмма столбиковая изображает статистические величины в форме удлиненных прямоугольников (столбиков). Столбиковая диаграмма — диаграмма одномерного измерения, поэтому все столбики по ширине должны быть одинаковыми, так как величина показателя характеризуется высотой столбика, и размещаться на горизонтальной прямой на равном расстоянии друг от друга. Пример столбиковой диаграммы, отражающей динамику застройки одного из районов г. Москва (Северное Бутово) приведен на рис.3.3.

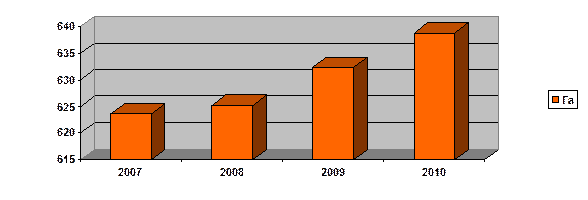
Рис.3.3. Динамика застройки одного из районов г. Москва (Северное Бутово) за 2007-2010 гг. [21]

Разновидностью полосовой диаграммы является скользящая диаграмма. В скользящей полосовой диаграмме направленность полос определяется не их нулевыми точками, а условными значениями, по которым полосы смещаются друг против друга вправо и влево. Полосовой скользящей диаграммой можно графически изобразить данные демографической статистики о вероятной продолжительности жизни людей в зависимости от пола и возраста.

Широкое применение имеют линейные диаграммы, которые иначе называются статистическими кривыми, и отражают изменение явления во времени.

При непрерывной вариации признака строятся интервальные вариационные ряды, графическим изображением которых является гистограмма. Для ее построения по оси абсцисс в соответствии с принятым масштабом откладывают границы интервалов признака. Эти интервалы являются основаниями прямоугольников, площади которых равны произведению величины интервалов на их частоты или частости.

В ряде случаев для изображения вариационных рядов используется кумулятивная кривая (кумулята). Для ее построения следует рассчитать накопленные частоты или частости, на оси абсцисс откладываются значения варьирующего признака, а на оси ординат помещаются накопленные частоты или частости. Например, имеются следующие данные о распределении семей по числу детей (цифры условные):

Таблица 3.1

Данные о распределении семей по числу детей (цифры условные)

Число детей в семье (х)	Численность семей в процентах к итогу (частость – f),%	Накопленная частость (s),%

Рис. 3.4.Кумулята распределения семей по числу детей, соответствующая данным табл.3.1.

Секторная диаграмма применяется для иллюстрации структуры изучаемой совокупности. Секторные диаграммы строятся по следующему принципу: вся величина явления принимается за 100%, затем считаются доли отдельных частей в процентах. Круг разбивается на секторы пропорционально частям изображаемого целого, т.е. на 1% приходится 3,6 градуса. Чтобы получить центральные углы секторов, отображающие доли частей целого, следует их процентное выражение умножить на 3,6 градуса Например, на рис. 3.5. показан характер возникновения ЧС в 2007 г.[19] (в 2009 г. произошла 270 ЧС техногенного характера, количество ЧС природного характера составило 133, произошла 21 биолого-социальная ЧС).

Рис. 3.5. Характер возникновения ЧС в 2007 г.[19]

Для одновременного изображения трех величин, связанных между собой таким образом, что одна величина является произведением двух других, применяются диаграммы, называемые знак Варзара (по имени русского статистика В.Е. Варзара) и представляет собой прямоугольник, у которого один сомножитель принят за основание, другой – за высоту, а вся площадь равна их произведению (рис.3.6). Например, имеются следующие данные, приведенные в табл. 3.2. (цифры условные):

Таблица 3.2

Показатели	Посевная площадь, млн. га	Урожайность, ц/га	Валовой сбор, млн. ц
Пшеница озимая	14,9	17,9	248,8
Пшеница яровая	39,4	18,2	717,1

Рис. 3.6.Валовой сбор озимой и яровой пшеницы

Графический метод в статистике является продолжением и дополнением табличного метода. График позволяет сравнительно легко обнаружить на глаз ошибки расчетов, которые в табличной форме не были так заметны. Незамеченными при чтении таблиц могут оставаться не только ошибки, но какие-то тенденции. Все это обнаруживается на графике. Статистические графики отражают целостную картину изучаемого явления, его обобщенное представление.

При графическом изображении статистических данных становится более выразительной сравнительная характеристика изучаемых показателей, отчетливее проявляется тенденция развития изучаемого явления, лучше видны основные взаимосвязи.

Анализ вариационных рядов

Одной из важных задач анализа рядов распределения является выявление закономерности распределения, определения ее характера и количественного выражения. Эта задача решается при помощи показателей, характеризующих форму, тип распределения.

Кроме рассмотренных выше важной характеристикой рядов распределения являются также моменты распределений.

Моментом распределения 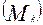называется средняя арифметическая из отклонений значений признака от некоторой постоянной величины в степени .

Порядок момента определяется величиной . Эмпирический момент -го порядка определяется по формуле

В зависимости от постоянной величины различают:

- начальные,

- центральные и

- условные моменты.

Если , то моменты называются начальными и определяются по формуле ;

В этом случае при получаем начальный момент нулевого порядка, который равен .

При 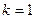получаем начальный момент первого порядка, который равен: ,

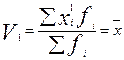при - начальный момент второго порядка, равный ,

и т.д.

Начальные моменты используются, в частности, при расчете дисперсии: .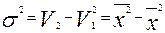

Если постоянная величина , то получим центральные моменты, которые определяются по формуле .

В этом случае при получим центральный момент нулевого порядка, который равен ,

при - центральный момент первого порядка, равный: ,

при - центральный момент второго порядка, равный: ; и т.д.

В формулах для вычисления условных моментов представляет собой определенное значение.

Анализ вариационных рядов предполагает выявление закономерностей распределения, определение и построение некой теоретической (вероятностной) формы распределения. Графическое изображение эмпирического вариационного ряда принимает вид плавной кривой, именуемой кривой распределения. Характер распределения лучше всего проявляется при большом числе наблюдений и малых интервалах.

Кривая распределения является обобщенной характеристикой особенностей формы распределения и выражает закономерность распределения единиц совокупности по величине варьирующего признака.

Различают кривые распределения эмпирические и теоретические.

Эмпирическая кривая — кривая распределения, полученная по данным наблюдения, которая отражает как общие, так и случайные условия, определяющие распределение.

Теоретическая кривая распределения — кривая, выражающая функциональную связь между изменением варьирующего признака и изменением частот и характеризующая определенный тип распределения.

Анализируя частоты в эмпирическом распределении, можно описать его с помощью математической модели — закона распределения, установить по исходным данным параметры теоретической кривой и проверить правильность выдвинутой гипотезы о типе распределения данного ряда. Нахождение функции кривой распределения называется моделированием.

При исследовании закономерностей распределения очень важно выдвинуть верную гипотезу о типе кривой распределения, так как, если кривая описана математически (с помощью уравнения) верно, она более точно отражает закономерности данного распределения и может быть использована в различных практических расчетах и прогнозах, в этом случае можно сформулировать рекомендации для принятия практических решений.

Для аппроксимации (выравнивания) эмпирических кривых распределения и сопоставления их с теоретическими в практике статистического исследования часто используют различные распределения: нормальное, логарифмически нормальное, биномиальное, Пуассона, Шарлье и др.

Каждое распределение имеет свою специфику и область применения. Далее будут рассмотрены только нормальное распределение и распределение Пуассона.

Нормальное распределение

При построении статистических моделей весьма широко применяется нормальное распределение.

В 1727 г. английский математик Абрахам де Муавр (1667—1754) открыл закон распределения вероятностей, названный законом нормального распределения. Позднее, в начале XIX в., разработкой вопросов, относящихся к данному закону, занимались Пьер Лаплас (1749-1827) и Карл Гаусс (1777-1855). Общие условия возникновения закона нормального распределения установил А.М.Ляпунов (1857-1918).

Распределение непрерывной случайной величины называют нормальным , если соответствующая ей плотность распределения выражается формулой

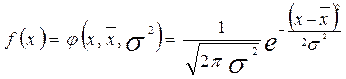
или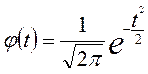

где:

	значение изучаемого признака
	средняя арифметическая ряда
	дисперсия значений изучаемого признака
	среднее квадратическое отклонение изучаемого признака
	нормированное отклонение

При графическом изображении плотности распределения получают кривую нормального распределения, симметричную относительно вертикальной прямой , поэтому величину называют центром распределения.

Случайные величины, распределенные по нормальному закону, различаются значениями параметров и , поэтому очень важно выяснить, как эти параметры влияют на вид нормальной кривой.

Если не меняется, а изменяется только , то:

1) чем меньше , тем более вытянута вверх кривая, а так как площадь, ограниченная осью и данной кривой, равна 1, то вытягивание вверх компенсируется сжатием около центра распределения и более быстрым приближением кривой к оси абсцисс;

2) чем больше , тем более плоской и растянутой вдоль оси абсцисс становится кривая.

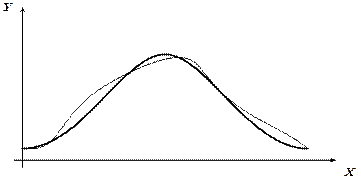
Рис. 3.7. Кривая нормального распределения теоретическая и экспериментальная

Если остается неизменной, а изменяется, то кривые нормального распределения имеют одинаковую форму, но отличаются друг от друга положением максимальной ординаты.

Особенности кривой нормального распределения.

1. Кривая симметрична и имеет максимум в точке, соответствующей значению .

2. Кривая асимптотически приближается к оси абсцисс, продолжаясь в обе стороны до бесконечности. Чем больше отдельные значения отклоняются от , тем реже они встречаются.

Кривая имеет две точки перегиба на расстоянии от .

Площадь между ординатами, проведенными на расстоянии (заштрихованная область на рис. 5.8, б), составляет 0,683. Это означает, что 68,3% всех исследуемых единиц (частот) отклоняется от средней арифметической не более чем на , т.е. находится в пределах . В промежутке 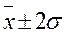находится 95,4%, а в промежутке , соответственно, 99,7% всех единиц исследуемой совокупности.

Коэффициенты асимметрии и эксцесса равны нулю.

Порядок расчета теоретических частот кривой нормального распределения:

1) по эмпирическим данным рассчитывают среднюю арифметическую ряда и среднее квадратическое отклонение ;

2) находят нормированное отклонение каждого варианта от средней арифметической:

3) по таблице распределения функции 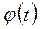определяют ее значения;

4) вычисляют теоретические частоты по формуле

где - объем совокупности, - длина интервала.

5) в случае, если вариационный ряд имеет равные интервалы,

Распределение Пуассона

К числу важнейших теоретических распределений, имеющих практическое применение, относится пуассоновское распределение, названное по фамилии французского математика Симеона Пуассона (1781-1840). Классическую форму распределение Пуассона принимает в том случае, если значения признака носят дискретный характер 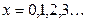и являются результатом какого-либо редко возникающего события среди наблюдаемых единиц. Причем с увеличением значений признака вероятность наступления события падает. Природа распределения Пуассона наиболее полно раскрывается в теории случайных процессов, поэтому его еще называют законом распределения редких явлений. Распределение Пуассона наблюдается в совокупностях, число единиц которых достаточно велико , а доля единиц, обладающих большими значениями признака, мала.

Аналитически распределение Пуассона можно выразить формулой:

где:

- вероятность того, что признак примет то или иное значение,

- средняя арифметическая ряда

Из формулы видно, что единственным параметром распределения является средняя арифметическая.

Порядок расчета теоретических частот кривой распределения Пуассона:

1) находят среднюю арифметическую ряда, т.е. ;

2) по таблицам определяют ;

3) для каждого значения вычисляют теоретическую частоту по формуле

где:

- число единиц в изучаемой совокупности.

Рис.3.8 Кривая распределения Пуассона

Кривые распределения бывают симметричными и асимметричными. В зависимости от того, какая ветвь кривой распределения вытянута — правая или левая — различают правостороннюю или левостороннюю асимметрию.

Кривые распределения могут быть одно-, двух- и многовершинными.

В нормальном ряду распределения размах вариации

; ;

Если указанные соотношения нарушены, то это свидетельствует о наличии асимметрии распределения.

При

разности между и положительные и асимметрия правосторонняя,

при ,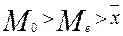

разности между и отрицательные и симметрия левосторонняя.

Коэффициент асимметрии равен отношению центрального момента третьего порядка к среднему квадратическому отклонению в кубе:

Если , то асимметрия правосторонняя, а если , то асимметрия левосторонняя. Чем числитель ближе к 0, тем асимметрия меньше.

В качестве показателя асимметрии применяется и коэффициент асимметрии Пирсона, представляющий собой отношение разности между средней арифметической и модой к среднему квадратическому отклонению:

Если , скошенность правосторонняя (как и для );

если , скошенность левосторонняя;

если , вариационный ряд симметричен

Крутизна, островершинность кривой распределения называется эксцессом.

Различают эксцессы: нормальный, выше нормального и ниже нормального.

Рис.3.9. Симметричная кривая распределения () и асимметричные кривые распределения (правосторонняя асимметрия и левосторонняя асимметрия ).

Для характеристики степени эксцесса применяют коэффициент эксцесса, который равен отношению центрального момента четвертого порядка к среднему квадратическому отклонению в четвертой степени: .

Рис. 3.10. Эксцессы распределения

Рис. 3.11. Изменение квадратического отклонения для кривых распределения с различным эксцессом

Если распределение нормальное, то эксцесс нормальный и равен 3. Если , то эксцесс выше нормального, а если , то эксцесс ниже нормального. На рис.7.5. показано изменение квадратического отклонения для кривых распределения с различным эксцессом.

Так как все предположения о характере того или иного распределения — это гипотезы, а не категорические утверждения, то необходима статистическая проверка с помощью так называемых критериев согласия. Критерии согласия, опираясь на установленный закон распределения, дают возможность установить, когда расхождения между теоретическими и эмпирическими частотами следует признать несущественными (случайными), а когда — существенными (неслучайными). Критерии согласия позволяют принять для данного эмпирического распределения модель, выраженную некоторым теоретическим законом распределения.

Существует ряд критериев согласия. Чаще других применяют критерии Пирсона, Романовского и Колмогорова.

Критерий согласия Пирсона (хи-квадрат) — один из основных критериев согласия, предложен английским математиком Карлом Пирсоном (1857—1936) для оценки случайности (существенности) расхождений между частотами эмпирического и теоретического распределений:

где:

	число групп, на которые разбито эмпирическое распределение;
	наблюдаемая частота признака в -й группе
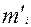
	теоретическая частота, рассчитанная по предполагаемому распределению.

Вычисление Пирсона связано с показателем, который называется числом степеней свободы. Под числом степеней свободы понимают количество независимых величин, которые могут принимать независимые значения, не изменяющие заданные характеристики.

Для распределения составлены таблицы, где указано критическое значение критерия согласия для выбранного уровня значимости и данного числа степеней свободы .

Уровень значимости — вероятность ошибочного отклонения выдвинутой гипотезы, т.е. вероятность того, что будет отвергнута правильная гипотеза. В статистических исследованиях в зависимости от важности и ответственности решаемых задач пользуются следующими тремя уровнями значимости:

1) 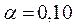, тогда

2) , тогда

3) , тогда

Например, вероятность 0,01 означает, что в одном случае из 100 может быть отвергнута правильная гипотеза. В экономических исследованиях считается практически приемлемой вероятность ошибки 0,05, т.е. в 5 случаях из 100 может быть отвергнута правильная гипотеза.

Кроме того, -критерий, определяемый по таблице, зависит и от числа степеней свободы.

Число степеней свободы определяется как число групп в ряду распределения минус число связей

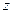
Под числом связей понимается число показателей эмпирического ряда, использованных при исчислении теоретических частот, т.е. показателей, связывающих эмпирические и теоретические частоты .

Так, в случае выравнивания по кривой нормального распределения имеется три связи:

, ,

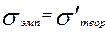Поэтому при выравнивании по кривой нормального распределения число степеней свободы определяется как , где — число групп в ряду.

В случае выравнивания по кривой Пуассона , так как при построении частот используются две ограничивающие связи: .

Для оценки существенности расчетное значение сравнивается с табличным .

При полном совпадении теоретического и эмпирического распределений , в противном случае .

Если 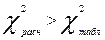то при заданном уровне значимости и числе степеней свободы гипотезу о несущественности (случайности) расхождений отклоняют.

В случае если заключают, что эмпирический ряд хорошо согласуется с гипотезой о предполагаемом распределении и с вероятностью можно утверждать, что расхождение между теоретическими и эмпирическими частотами случайно.

Используя критерий согласия , необходимо соблюдать следующие условия:

1) объем исследуемой совокупности должен быть достаточно большим , при этом частота или численность каждой группы должна быть не менее 5. Если это условие нарушается, необходимо предварительно объединить маленькие частоты;

2) эмпирическое распределение должно состоять из данных, полученных в результате случайного отбора, т.е. они должны быть независимыми.

Критерий Романовского основан на использовании критерия Пирсона (найденных значений ) и числа степеней свободы :

Он весьма удобен при отсутствии таблиц для .

Если , то расхождения между теоретическим и эмпирическим распределением случайны, если же , то не случайны и, соответственно, теоретическое распределение не может служить моделью для изучаемого эмпирического распределения.

Критерий Колмогорова основан на определении максимального расхождения между накопленными частотами или частостями эмпирических и теоретических распределений:

или

где и — соответственно максимальная разность между накопленными частотами и между накопленными частостями эмпирического и теоретического рядов распределений; — число единиц в совокупности.

Рассчитав значение , по таблице определяют вероятность, с которой можно утверждать, что отклонения эмпирических частот от теоретических случайны. Вероятность может изменяться от 0 до 1. При происходит полное совпадение частот, при 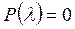- полное расхождение. Если принимает значения до 0,3, то .