 |
Раздел 5. Исследование рядов динамики
|
|
|
|
Ряды динамики и их анализ
Ряд последовательно расположенных в хронологическом порядке статистических показателей, характеризующих изменение какого-либо явления во времени образует ряд динамики (динамический ряд, временной ряд), элементамикоторого являются: 1) время и 2) конкретные значения показателя (уровень ряда).
Уровни интервальных рядов динамики можно складывать, полученные в результате суммирования данные, имеют вполне реальное содержание, при сложении уровней образуются новые, более укрупненные члены динамического ряда. Уровни моментного ряда суммировать нельзя.

Рис. 5.1. Основные виды рядов динамики
Еслиосновные характеристики случайного процесса(математическое ожидание значения признака, дисперсия) не зависят от времени (постоянны), то процесс считается стационарным. В случае, когда зависимость от времени основных характеристик процесса существует, ряд называют нестационарным.
Ряды динамики удобно представлять в виде таблиц и графиков, при этом важно выявить основную закономерность в изменении уровней ряда - тренд.
Например, на рис.5.2. показана Ежемесячная динамика экспорта из РФ в Республику Казахстан в стоимостном выражении (млн.долл.), 2009-2010 гг.

Рис. 5.2. Ежемесячная динамика экспорта из РФ в Республику Казахстан в стоимостном выражении (млн.долл.), 2009-2010 гг.[20]
Условием правильности построения рядов динамики является обеспечение сопоставимости данных. Построение и анализ рядов динамики позволяют выявлять закономерности развития явлений, вскрываются особенности их развития (периодические и сезонные колебания и т.д.). При сравнении нескольких динамических рядов целесообразно изображать их на одном графике.
|
|
|
Смыкание рядов динамики (приведение моментных рядов динамики к сопоставимому виду) необходимо в ряде случаев при сопоставлении экономических показателей, уровни которых исчислены по разным методологиям или в разных границах. Для осуществления такого смыкания необходимо, чтобы данные одного из периодов были исчислены по двум методологиям. При этом используются следующие способы:
1. По данным рядов определяется коэффициент соотношения уровней переходного периода (момента) делением нового уровня на старый уровень (при этом уровни относятся к одному периоду времени, в котором произошло изменение методологии расчета). Полученный коэффициент соотношения уровней показывает во сколько раз изменился новый уровень по сравнению со старым. Затем данные за предшествующий изменению период умножаются на полученный коэффициент соотношения, получая условно сопоставимые уровни.
2. Уровни переходного периода принимаются для каждого из смыкаемых рядов за 100%, а остальные пересчитываются в процентах по отношению к этим уровням. Таким образом все уровни заменяются базисными темпами роста, когда за базу принят уровень переходного периода.
Средняя интервального ряда вычисляется как средняя арифметическая простая.
Средний уровень для моментного ряда с равноотстоящими во времени уровнями (промежутки между датами равны), вычисляются по формуле средней хронологической:
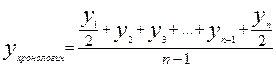
где:
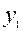 - начальный уровень ряда
- начальный уровень ряда
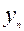 - конечный уровень ряда
- конечный уровень ряда
 - число дат
- число дат
Средний уровень для моментного и интервального ряда с неравными во времени уровнями (промежутки между датами различны), вычисляются по формуле средней арифметической взвешенной.

Для более подробной характеристики изменения уровней динамических рядов применяются следующие показатели: абсолютный прирост  , коэффициент роста
, коэффициент роста 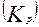 , коэффициент прироста
, коэффициент прироста 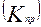 , темп роста
, темп роста  , темп прироста
, темп прироста 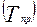 , абсолютное значение 1% прироста
, абсолютное значение 1% прироста 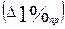 .
.
|
|
|
Абсолютный прирост характеризует размер увеличения (или уменьшения) уровня ряда за определенный период времени. Он равен разности двух сравниваемых уровней, показывает абсолютную скорость роста и выражается в единице изменения ряда:
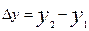
Коэффициент роста 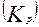 есть отношение последующего уровня к предыдущему:
есть отношение последующего уровня к предыдущему: 
Коэффициент прироста равен коэффициенту роста минус единица:

Темп роста рассчитывается так же, как и коэффициент роста, только результат выражается не в коэффициентной, а в процентной форме.

Темп прироста равен темпу роста минус 100%:
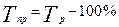
Абсолютное значение 1% прироста равно абсолютному приросту, деленному на темп прироста:
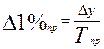
Этот показатель получается в тех же именованных числах, что и уровни ряда.

Рис. 5.3. Методы расчета показателей рядов динамики
При расчете базисным методом все уровни ряда относятся к уровню одного какого-либо периода, принятого им за базу, то есть за 100% или за единицу:
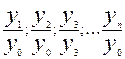
При расчете цепным методом уровень каждого периода относится к уровню предыдущего периода:

Цепные и базисные темпы роста находятся во взаимосвязи .
1. Если последовательно перемножить цепные темпы роста (взятые в коэффициентной форме), получим базисные темпы роста.
2. Можно преобразовать и базисные темпы роста в цепные, разделив. каждый последующий темп роста на предыдущий базисный темп роста.
Обобщающей характеристикой интенсивности развития за длительный период времени являются среднегодовые темпы роста, вычисленные по формуле средней геометрической.

 - число лет, включая и базисный период.
- число лет, включая и базисный период.
Если рассчитаны ежегодные коэффициенты роста продажи товаров (например, реализация швейных изделий по региону на человека цепным способом), то для расчета среднего темпа роста можно использовать другую формулу средней геометрической:

Например, коэффициенты роста продажи швейных изделий по региону на человека каждого последующего года по сравнению с предыдущим составили: 1,065; 1,055; 1,042; 1,036; 1,005.
Средний темп роста  равен:
равен:
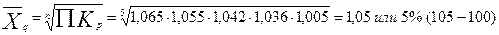
Таким образом, ежегодный средний прирост продажи швейных изделий по региону за 5 лет увеличивается на 5%.
|
|
|
Вычисление коэффициента опережения динамических рядов дает возможность установить интенсивность изменения одного явления по сравнению с другим во времени и исчисляется как отношение базисных темпов роста двух динамических рядов за одинаковые отрезки времени. Вычисление производят по следующей формуле:
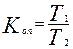
где:
 - темп роста первого динамического ряда;
- темп роста первого динамического ряда;
 - темп роста второго динамического ряда.
- темп роста второго динамического ряда.
Теоретически при анализе рядов динамики рассматриваются:
- тренд (тенденция) – общее направление в изменении уровней ряда, о сновная (устойчивая) тенденция развития явления (рост, снижение или стабилизация в течении времени);
- периодически повторяющиеся колебания (долговременные циклические колебания, кратковременные или сезонные колебания);
- случайные колебания под влиянием внешних факторов.
Для анализа динамических рядов используются следующие основные методы: расчет по имеющимся данным за определенный период некоторых недостающих значений внутри этого периода (интерполяция), расчет прогнозного значения (экстраполяция).
Выявление основной тенденции развития динамического ряда в статистике называют выравниванием ряда динамики, при этом используются: метод укрупнения интервалов, метод скользящей средней, аналитическое выравнивание.
Метод укрупнения интервалов предполагает переход от первоначального динамического ряда к ряду, промежутки времени которого больше, например, квартальные данные заменяются годовыми. По укрупненным интервалам суммируют уровни первоначального ряда или рассчитывают средние величины, что позволяет сглаживать отклонения, возникающие за счет случайных причин и выявлять общую тенденцию развития динамического ряда. Для моментных рядов, а также, если уровни ряда выражены относительной или средней величиной, суммирование уровней не имеет смысла, а по укрупненным интервалам рассчитывают средние показатели.
При укрупнении интервалов число уровней ряда динамики существенно сокращается и не учитывается изменение уровней внутри укрупненных интервалов, поэтому для более детальной характеристики тенденции изменения уровней используют выравнивание динамических рядов методом скользящей средней.
|
|
|
Метод скользящей средней заключается в расчете средних уровней по укрупненным интервалам путем последовательного смещения начала отсчета на единицу времени, исключая постепенно из интервала первые уровни и включая последующие, например:
- для первого интервала
 ;
;
- для второго интервала
 ;
;
- для третьего интервала
 .
.
В результате сглаживания получается ряд динамики, количество уровней которого на два меньше, чем у исходного (теряются два крайних значения).
Число уровней, по которым рассчитывают скользящую среднюю, называют периодом (интервалом сглаживания), чем он меньше, тем точнее сглаженный ряд отражает исходный. Выбор периода сглаживания осуществляется в зависимости от характера колебаний уровней фактического динамического ряда. Если колебания имеют определенную периодичность, то период сглаживания следует принять равным или кратным периоду колебаний. Предпочтительнее применять период сглаживания с нечетным количеством уровней, поскольку расчетное значение уровня будет в центре числа слагаемых скользящей средней и им легко заменить фактическое значение. При использовании четного периода сглаживания необходимо применение специальной процедуры центрирования, заключающейся в нахождении средней из двух смежных скользящих средних, позволяя соотнести полученный уровень с определенной датой.
Метод аналитического выравнивания динамического ряда заключается нахождении аналитической функции, характеризующей зависимость уровней ряда от времени. Предварительно проводят анализ потенциально приемлемых функций, чаще на основе графического изображения динамического ряда. Современные компьютерные технологии позволяют аппроксимировать ряды динамики линейной, логарифмической, полиномиальной, степенной и экспоненциальной функциями.
Аналитическое выравнивание динамического ряда линейной зависимостью
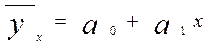 ,
,
где
 - уровень, найденный по уравнению;
- уровень, найденный по уравнению;
 и
и  - параметры уравнения, которые при применении способа наименьших квадратов находятся из решения системы нормальных уравнений;
- параметры уравнения, которые при применении способа наименьших квадратов находятся из решения системы нормальных уравнений;
 - время или иной аргумент.
- время или иной аргумент.
Используя метод наименьших квадратов, получаем систему уравнений вида:

В результате решения системы уравнений определяются коэффициенты уравнения.
Выравнивание линейной зависимостью применяется в том случае, когда изменение уровня ряда динамики происходит с постоянной скоростью (например, в среднем сохраняет постоянство абсолютных приростов).
|
|
|
Аналогичным образом осуществляется аппроксимация другими математическими функциями.
Изменение экономических показателей часто характеризуется сезонными колебаниями рядов динамики, которые отражают одинаковые колебания явлений на протяжении изучаемого периода, например, из года в год в определенные месяцы уровень явления повышается, а в другие — снижается. Сезонность и сезонные колебания в экономике Российской Федерации вызываются как социальными, так и естественно-климатическими причинами. В свою очередь естественно-климатические причины оказывают неодинаковое воздействие на производство.
При изучении сезонных колебаний (сезонных волн) выявляют общую тенденцию развития явления внутри года и измеряют сезонные колебания изучаемого явления, при этом могут быть использованы метод построения «сезонной волны» и гармонический анализ.
В первом случае для анализа сезонных колебаний применяется индекс сезонности, порядок расчета которого зависит от стационарности или нестационарности ряда динамики.
Расчет индекса сезонности в стационарных рядах динамики заключается в нахождении простой средней арифметической за одни и те же внутригодовые промежутки времени всего изучаемого периода и в последующем сопоставлении полученных средних с общей средней динамического ряда.
Расчет индекса сезонности в нестационарных рядах динамики (при наличии тренда) следующий:
- определяют по одноименным внутригодовым (квартальным, месячным) уровням ряда за несколько лет (кварталов, месяцев) на основе метода скользящей средней или методом аналитического выравнивания расчетные уровни ряда;
- находят процентное отношение фактических уровней ряда и расчетных уровней ряда;
- усредняют полученные показатели сезонности
Совокупность средних индексов сезонности одноименных периодов составляет модель сезонной волны.
Гармонический анализ основан на представлении ряда динамики в виде совокупности колебательных процессов, описываемых с помощью гармонического ряда Фурье.
Во многих рядах динамики наблюдается зависимость уровня t от уровня t-1. Такая зависимость между соседними (последовательными) уровнями ряда называется автокорреляцией, которая может быть представлена уравнением авторегрессии. В ряде случаев при исследовании взаимосвязей между исследуемыми показателями бывает необходимо устранять влияния автокорреляции.
|
|
|


