Выборочный метод в изучении социально-экономических явлений и процессов

При выборочном методе наблюдению подвергается не вся совокупность единиц, а только часть их, отобранная на основе определенных научно обоснованных принципов. Выборочное наблюдение является одним из видов несплошного статистического наблюдения. Теория и практика применения выборочного метода показали, что данные выборочного наблюдения достаточно достоверны, так как выборочный метод базируется на применении закона больших чисел и теории вероятности.

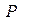Вся изучаемая статистическая совокупность, из которой производится отбор некоторого числа единиц для выборочного наблюдения, называется генеральной совокупностью ( - численность (объем) генеральной совокупности), - генеральная доля, полученная как отношение числа 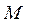единиц, обладающих данным признаком, ко всей численности 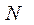генеральной совокупности, т.е.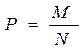

Часть генеральной совокупности, подлежащая выборочному обследованию, называется выборочной совокупностью (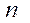 численность выборочной совокупности).

ω – выборочная доля (частость) — отношение числа 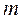единиц выборочной совокупности, обладающих данным признаком, ко всей численности 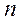выборочной совокупности.

Сущность выборочного метода заключается в том, что данные, полученные на основе отобранной части совокупности, распространяют на всю генеральную совокупность. В таблице 4.1. приведены основные обозначения, использованные в разделе 4.

Таблица 4.1.

Показатель	Совокупность
генеральная	выборочная
Число единиц (объем) совокупности
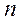
Среднее значение признака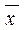
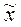
Доля единиц, обладающих изучаемым признаком		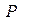ω
Доля единиц, не обладающих изучаемым признаком	q	1- ω
Дисперсия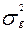
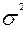
Среднее квадратическое отклонение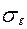

 

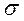
Разработана теория выборочного метода и доказывается, что при случайном отборе единиц выборочной совокупности среднее значение изучаемого признака (доли) в выборочной совокупности стремится к характеристикам генеральной совокупности, то есть по величине среднего значения признака (доли) в выборочной совокупности можно судить о среднем значении этого признака (доли) в генеральной совокупности.

Однако, из-за наличия ошибок репрезентативности, значения генеральной и выборочной средней всегда различаются на величину ошибки выборки, которая не превосходит величины предельной ошибки выборки.

Изучение вариации признаков в совокупности при проведении выборочного наблюдения приобретает особое значение.

Теория и практика статистической работы показывают, что средние и относительные величины, полученные по части единиц генеральной совокупности, достаточно точно воспроизводят соответствующие показатели совокупности, позволяя использовать метод выборочного наблюдения с целью экономии затрат времени и труда. Вместе с тем, выборочное наблюдение дает возможность значительно расширить программу статистического наблюдения и делать его более детальным, так как исследованию подвергается сравнительно небольшая часть совокупности.

Две основные задачи выборочного наблюдения:

1) определение среднего размера изучаемого признака и

2) определение доли изучаемого признака в данной совокупности.

При проведении выборочного наблюдения (поскольку проведение сплошного наблюдения заменяется выборочным) важно установить, насколько средняя выборочная является характерной для данной генеральной совокупности, необходимо установить, как велико отклонение 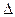средней выборочной от средней генеральной , т.е. .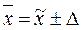

Чем меньше величина отклонения 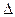, тем точнее выборочная средняя воспроизводит генеральную среднюю. Величина этого отклонения и определяет степень точности выборочного наблюдения.

Задача выборочного метода заключается в том, чтобы, с достаточной достоверностью определить среднее значение изучаемого признака по всей совокупности, поэтому понятно значение отбора единиц из генеральной совокупности. Различают следующие виды отбора единиц в выборочную совокупность.

Случайный отбор. Принцип случайного отбора состоит в том, что единицы для наблюдения отбираются из всей генеральной совокупности, при этом каждая единица генеральной совокупности имеет равную возможность попасть в выборочную совокупность. В таком случае среднее значение изучаемого признака окажется представленным достаточно точно.

Случайный отбор может быть повторным и бесповторным.

Бесповторным называется такой отбор, когда отобранная единица не возвращается обратно в генеральную совокупность. Следовательно, численность генеральной совокупности с каждой отобранной единицей сокращается.

На практике повторный отбор осуществляется редко (отобрав однажды образец товара для исследования его качества, вновь в выборку он возвратиться чаще всего не может). Практика выборочного метода обычно использует бесповторный отбор. Однако приведенные ранее формулы средней ошибки выборки выведены для условий повторной выборки. При бесповторной выборке под корнем нужно добавить множитель 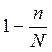. Так как 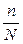всегда положительная дробь, то этот множитель всегда меньше единицы. Это означает, что бесповторная выборка точнее, чем повторная. В то же время этот множитель близок к единице (при 5%-й выборке он равен 0,95, при 10%-й — 0,90 и т.д.). Последнее приводит к тому, что для упрощения расчета при случайном бесповторном отборе пользуются той же формулой средней ошибки, что и при случайном повторном отборе, т.е. 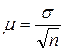, преувеличивая при этом несколько ошибку выборки.

Механический отбор. При механическом отборе, основанном на принципе случайного отбора, из генеральной совокупности отбирается определенное число единиц через определенный интервал (каждая пятая, десятая, пятнадцатая, двадцатая и т.д.). Генеральную совокупность механически разбивают на равные группы, число которых равно численности выборочной совокупности.

Широко применяется механический отбор при контроле качества различных продуктов, например, для анализа качества механически отбирается из партии каждая пятидесятая единица, затем производится лабораторный анализ отобранных единиц. Средняя ошибка выборки при механическом отборе определяется по тем же формулам, как и при повторном случайном отборе.

Типический отбор. Для получения более точных данных выборочного наблюдения всю генеральную совокупность разбивают на отдельные типические группы по какому-либо признаку. Выбор типических признаков производится на основе анализа изучаемой совокупности. Внутри группы проводится случайный или механический отбор. При таком способе отбора гарантировано попадание в выборку представителей всех типических групп, что повышает её репрезентативность (представительность).

Типические группы по численности единиц могут быть не равны между собой. В таком случае отбор, как правило, производится пропорционально к объему группы. Например, типологический отбор может быть применен для определения качества товар поступавшего неравными партиями.

Отобранное по каждой группе количество единиц является частной выборочной совокупностью. Для каждой такой выборочной совокупности можно установить средний размер изучаемого признака и среднее квадратическое отклонение, которое характеризует внутригрупповую вариацию признака в пределах своей группы, затем найти показатель внутригрупповой вариации признака для всех групп совокупности, вместе взятых.

Чтобы получить общую выборочную среднюю для всех обследованных групп, надо, зная частные выборочные средние, получить среднюю арифметическую взвешенную, причем в качестве весов можно взять или общую численность каждой группы, или численность выборки в каждой группе. Результат будет одинаковый, так как количество обследуемых единиц распределяется по группам пропорционально их удельному весу в общей совокупности.

Ошибка выборки при типическом отборе определяется по той же формуле, что и при случайном отборе, однако вместо общей дисперсии признака в этой формуле участвует средняя дисперсия из внутригрупповых дисперсий.

Серийная (гнездовая) выборка в практике выборочного наблюдения заключаетсяв отборе целых групп единиц (гнездо), а затем внутри отобранных групп подвергают наблюдению все единицы без исключения. Серийный отбор имеет большое практическое значение, так как легче организовать отбор и изучение нескольких серий, чем большого количества отдельных единиц. Для отбора серий применяют либо случайную выборку, либо механический отбор.

Ошибки репрезентативности, возникающие при выборочном наблюдении, определяются спецификой самого метода и именно потому, что обследуется не вся совокупность, а лишь его часть, отобранная в случайном порядке. Следовательно, определение достоверности данных выборочного наблюдения, является основной задачей теории выборочного исследования.

Сущность закона больших чисел заключается в том, что чем больше будет взято единиц под наблюдение, тем точнее средняя выборочная будет воспроизводить среднюю генеральную. Теория выборочного метода дает формулу, по которой можно вычислить среднюю величину ошибки для выборочной совокупности, отобранной в случайном порядке, т.е. таким образом, что каждая единица генеральной совокупности имела бы равную возможность попасть в это число:

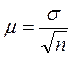
где: 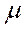- средняя ошибка выборки.

Величина средней ошибки выборки зависит прежде всего от показателей вариации значений признаков в выборочной совокупности. Чем меньше величина среднего квадратического отклонения (следовательно, чем однороднее совокупность), тем меньше величина средней ошибки при той же численности выборки.

Кроме того, величина средней ошибки зависит от численности выборки. Увеличивая или уменьшая объем выборки, можно регулировать величину ошибки. Чем больше единиц будет охвачено выборочным наблюдением, тем меньше будет величина ошибки, характеризующей среднее отклонение средней выборочной от средней генеральной, так как тем точнее будет представлена генеральная совокупность. В практике применения выборочного метода ставится задача определения пределов, за которые не выйдет величина конкретной ошибки выборочного наблюдения, и зависящая

от степени вероятности, с которой измеряется ошибка выборки. Ошибка выборки, исчисленная с заданной степенью вероятности, представляет предельную ошибку выборки. Перед проведением выборочного наблюдения, устанавливают необходимую численность выборки, т.е. объем выборки, необходимый для того, чтобы обеспечить результаты выборочного наблюдения с заранее установленной точностью. Необходимая численность выборки определяется на основе формул предельной выборки. Распространение выборочных данных на генеральную совокупность является конечной задачей выборочного наблюдения. Основные формулы, используемые при проведении выборочного наблюдения, представлены в таблицах 4.2-4.4.

Таблица 4.2.

Формулы средней ошибки выборки при собственно случайном и механическом отборе

Оцениваемый параметр	Повторный отбор	Бесповторный отбор
Средняя
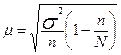
Доля

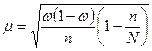
Алгоритм определения ошибки выборки

1. По результатам выборочного наблюдения производится расчет среднего значения (доли) признака в выборочной совокупност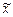и– или .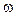

2. Определяется дисперсия признака. Расчет удобнее производить по формулам: для средней 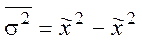_, для доли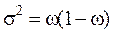

3. В соответствии с использованным способом отбора исчисляется величина средней ошибки выборки .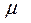

4. По таблице закона нормального распределения, в соответствии с заданной величиной вероятности ошибки выборки определяется величина коэффициента доверия .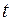

5. По формуле исчисляется величина предельной ошибки выборки .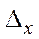

6. По формулам исчисляются границы возможного колебания выборочной средней границы, в которых находится величина генеральной средней.

Таблица 4.3.

Формулы средней ошибки выборки при типическом отборе

 

Пропорциональное распределение единиц выборочной совокупности по группам
Оцениваемый параметр	Повторный отбор	Бесповторный отбор
Средняя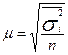
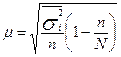
Доля

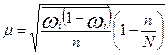
⇐ Предыдущая45678910111213Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: