Оптимальный рост: формулы критерия Келли для практиков

Критерий Келли в блек-джеке, спортивных тотализаторах и на фондовой бирже.

Эдвард О. Торп

Примечание перев.: замечания по переводу принимаются по адресу mails@fromru.com (Киселев Дмитрий).

В данной редакции отсутствуют приложения – см. оригинал на англ.:

Abstract, Chapters 1 - 10 (2.5M)

Figures, Appendices, and References (750K)

 

Аннотация

Центральная проблема для игроков – найти и заключить пари с положительным ожидаемым выигрышем. Но игрокам также необходимо знать, как управлять их деньгами, т.е. сколько ставить. На фондовых рынках (включая рынок ценных бумаг) проблема подобна этой, но более сложна. Игрок, который теперь является инвестором, ищет «большую прибыль при управляемом уровне риска». В обоих этих случаях, мы исследуем использование критерия Келли, который максимизирует ожидаемую величину логарифма дохода («максимизирует ожидаемую логарифмическую полезность»).

Этот критерий известен экономистам и теоретикам-финансистам под такими именами как «стратегия максимизации геометрического среднего портфеля», максимизация логарифмической полезности, стратегия оптимального роста, критерий роста капитала и т.д.

Автор начал практическое применение критерия Келли с использования его для счета карт в блэк-джеке. Мы представим некоторые полезные формулы и методы, чтобы ответить на различные естественные вопросы об этом, которые возникают в блэк-джеке и других азартных играх. Затем мы проиллюстрируем его недавнее использование в успешных системах ставок для спортивных тотализаторов. В заключении, мы обсудим его приложение к рынку ценных бумаг, где эти методы помогли автору сделать за тридцать лет в общей сложности «ставок» на сумму 80 миллиардов долларов.

Пересмотрено 29 мая 1998 года

Введение

Фундаментальной проблемой в играх является поиск возможностей ставок с положительным ожиданием. Аналогичная проблема в инвестировании – поиск возможностей инвестирования с «избыточной», с учетом поправок на риск, доходностью. Как только такие благоприятные возможности идентифицированы, игрок или инвестор должен решить, какую часть своего капитала поставить на кон (вложить). Именно эту проблему мы здесь рассматриваем. Интерес к ней существует по крайней мере с восемнадцатого столетия, с обсуждения Даниилом Бернулли Санкт-Петербургского Парадокса (Feller, 1966).

Один подход состоит в том, чтобы минимизировать вероятность «потерять все» в пределах определенного числа попыток N. Примером другого подхода будет - максимизировать вероятность достижения установленной цели за N попыток (Browne, 1996).

Другой подход, наиболее изученный экономистами и не только, состоит в том, чтобы оценить деньги, используя функцию полезности. Она обычно определена для всех неотрицательных вещественных чисел, имеет вещественные значения и является не убывающей (большее количество денег по крайней мере столь же хорошо как меньшее количество денег). Некоторые примеры - U(x) = x^α, 0 ≤ α < ∞ и U(x) = log x, где log означает log_e, а log 0 = -∞. Как только функция полезности определена, цель состоит в том, чтобы максимизировать ожидаемую величину полезности капитала.

Даниил Бернулли использовал функцию полезности log x, чтобы "решить" Cанкт-Петербургский Парадокс. (Но решение не устраняет парадокс, потому что каждая функция полезности, которая не ограничена сверху, включая log, представляет собой измененную версию Санкт-Петербургского Парадокса.) Функция полезности log x была вновь использована J.L. Kelly (1956), показавшим, что она имеет некоторые замечательные свойства. Они были изучены и обобщены в исследовании Brieman (1961). Markowitz (1961) применяет ее к ценным бумагам. Дускуссии о критерии Kelly ("критерий среднего геометрического") с точки зрения финансов, см. McEnally (1986), там же приводятся дополнительные исторические справки и ссылки.

Меня со статьей Kelly познакомил Claude Shannon в Массачучетском Технологическом (M.I.T) в 1960, вскоре после того, как я создал математическую теорию счета карт для блэк джека. Критерий Келли заключался в нахождении величины ставки для каждой попытки, такой что она максимизировала E [log X], ожидаемую величину логарифма капитала X (случайная переменная). Я использовал его в реальной игре и представил это сообществу игроков в первом издании "Beat the Dealer", Thorp, (1962). Если все ставки блэк джека имеют положительное ожидание и независимы, ставки Келли, при игре на одну сдачу будут чрезвычайно просты: ставьте долю вашего текущего капитала, равную вашему ожиданию. На практике эта оценка несколько меняется (как правило снижается) для того, чтобы допустить возможность "ждущих ставок", имеющих некоторое отрицательное ожидание, при более высоких колебаниях, возникающих из-за выплат, больших, чем один к одному, и когда играются больше одной сдачи одновременно.

Вот свойства, которые сделали критерий Келли столь привлекательным. Для простоты понимания мы проиллюстрируем его на примере самого простейшего случая - подбрасывания монеты, но концепция и выводы легко обобщаются.

Подбрасывание монеты

Допустим, мы играем с бесконечно богатым противником, который будет делать повторяющиеся ставки на независимые события – броски монеты. Далее, предположим, что при каждом броске наша вероятность победы p> 1/2, а вероятность потери q = 1 - p. Наш начальный капитал - X_O. Предположим, что наша цель – максимизация ожидаемой величины E (X_n) через n попыток. Сколько мы поставим, B_{k ,} на k -ой попытке? Пусть T_k = 1, если k -я попытка - выигрышная и T_k = -1, если она проиграна, тогда X_k =X_k-1 + T_k B_k для k = 1,2,3.., и X_n = X_O + Σ ⁿ_k=1T_kB_k. Тогда

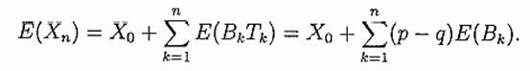
Так как игра имеет положительное ожидание, то есть p-q> 0, в этой ситуации равных выплат, для того, чтобы максимизировать Е(Х_n), мы должны были бы максимизировать E(B_k) для каждой попытки. Таким образом, чтобы максимизировать ожидаемый рост мы должны ставить все наши ресурсы в каждой попытке. Таким образом, B₁ = X₀, и, если мы выигрываем первую ставку, B₂ = 2X₀, и т.д. Однако, вероятность краха при этом будет 1 - p^N и при p < 1, lim _n→∞ [1 —рⁿ] = 1, так что крах почти неизбежен. Таким образом, "смелый" критерий ставок для максимизации ожидаемого роста обычно нежелателен.

Аналогично, если наша стратегия состоит в том, чтобы минимизировать вероятность возможного краха (а "крах" происходит, если X_K = 0 на k-ой попытке) широко известная формула краха игрока (по Feller (1966)) показывает, что мы минимизируем крах, делая минимальную ставку на каждой попытке, но это, к сожалению, также минимизирует и ожидаемый рост. Таким образом, "робкая" система ставок также непривлекательна.

Это предполагает существование промежуточной стратегия, которая лежит где-то между максимизацией E (X_n) (и верным крахом) и уменьшением вероятности краха (и уменьшением E (Х_n)). Асимптотически оптимальная стратегия была впервые предложена J.L. Kelly (1956).

Так как вероятности и выплаты при каждой ставке в описанной игре с подбрасыванием монеты одинаковы, кажется вполне правдоподобно, что "оптимальная" стратегия потребует всегда держать пари на одну и ту же долю f вашего капитала. Чтобы это было возможным сделать, мы предполагаем далее, что капитал может бесконечно дробиться. Это предположение обычно не имеет большого значения в практическом применении.

Стратегия, в которой ставки делаются согласно B_i = f X_i-1, где 0 ≤ f ≤ 1, иногда называется стратегией "фиксированной доли". Пусть S и F - числа успехов и проигрышей в n попытках соответственно, тогда наш капитал после n попыток равен X_n = X_o(1+ f)^S (1-f)^F, где S + F = n. При f в интервале 0 < f < 1, Рr (Х_n = 0) = 0. Таким образом, "краха", понимаемом в техническом смысле как разорение игрока, произойти не может. "Крах" впредь будет означать, что для произвольно маленького положительного ε, lim_n→∞[Рr(X_n ≤ ε)] = 1. В этом смысле, как мы увидим, крах все-таки может случиться при некоторых обстоятельствах.

Отметим, что так как

величина

измеряет экспоненциальную скорость роста за попытку. Kelly максимизировал ожидаемую величину коэффициента скорости роста, g(f), где

 

Обратите внимание, что g(f) = (1/n)E[logX_n]- (1/n)logX₀, поэтому, для фиксированного n, максимизация g(f) - то же самое, что максимизация E[logX_n]. В дальнейшем обсуждении мы в основном будем говорить о максимизации g(f). Заметим, что

когда f = f ^* = p - q.

Так как

то g' (f) убывает строго монотонно на [0, 1), Так как g' (0) = p-q > 0 и lim _f→1 - g'(f) = - ∞. Вследствие непрерывности g'(f), g (f) имеет единственный максимум в точке f=f *, где g(f *) = p log p + q log q + log 2 > 0. Более того, поскольку g(0) = 0 и lim _f→1 - g{f) = - ∞, то существует единственное f_C > 0, такое что 0 < f* < f_C < 1 и g(f_C) = 0. Природа функции g(f) теперь очевидна, и график g(f) от f выглядит так, как показано на Рисунке 1.

Следующая теорема излагает важные преимущества максимизации g(f). Детали здесь опущены, но доказательства (i), (ii), (iii), и (vi) для простого биномиального случая могут быть найдены в Thorp (1969); более общее доказательство этого, а также доказательства (iv) и (v) можно найти у Breiman (1961).

Теорема 1 (i) Если g(f) > 0, тогда почти достоверно, что lim_n→∞ Х_n = ∞, то есть для каждого М, Pr [lim _n→∞ inf Х_n > М] = 1;

(ii) если g(f) < 0, тогда почти достоверно, что lim_n→∞ Х_n = 0, то есть для каждого ε>0, Pr [lim _n→∞ sup Х_n < ε] = 1;

(iii) Если g(f) = 0, тогда почти достоверно, что lim _n→∞ sup Х_n= ∞ и lim _n→∞ inf Х_n = 0.

(iv) Для заданной стратегии Ф*, которая максимизирует E[log X_n] и любой другой "существенно иной" стратегии Ф (не обязательно стратегии фиксированных дробных ставок) почти достоверно, что lim_n→∞ Х_n(Ф*)/Х_n (Ф) = ∞.

(v) Ожидаемое время, необходимое чтобы текущий капитал X _n достиг заранее установленного значения С будет, асимптотически, наименьшим при стратегии, которая максимизирует E[log X_n].

(vi) Предположим, что отдача от одной ставки на i-ой попытке - биноминальная случайная переменная U_i, далее предположим, что вероятность успеха p _i, где 1/2 < p_i < 1. Тогда E[log X_n] максимизируется выбором значением для ставки при каждой попытке доли f *_i = p_i - q_i которая максимизирует E[ log (1+f_iU_i)].

Часть (i) показывает что, если бы не конечное время, благосостояние игрока X_N превысило бы любой установленный предел М, когда f выбрано в интервале (0, f _с). Но, если f > f _C, часть (ii) показывает, что крах почти неизбежен. Часть (iii) демонстрирует, что, если f = f _C, Х_n будет (почти достоверно) беспорядочно колебаться между 0 и + ∞, Таким образом, утверждение одного из авторов, что X_n → X₀ при n → ∞, когда f = f_с, явно противоречиво. Части (iv) и (v), показывают, что стратегия Kelly максимизирования E[logX_n] является асимптотически оптимальной в соответствии с двумя важными критериями. "Существенно иная " стратегия - одна из таких, что разница E[ ln X_n*] – E[ lnX_n] между стратегией Kelly и другой стратегией растет быстрее, чем стандартное отклонение ln X_n* - ln X _n, обеспечивая Р (ln X_n* - ln X _n > 0) → 1. Часть (vi) устанавливает справедливость использования метода Kelly выбора f_i* при каждой попытке (даже если от одной попытки к следующей меняется вероятность) для максимизации E[log X_n].

Пример 2.1 Игрок А играет против бесконечно богатого противника. Игрок выигрывает одну и ту же сумму при последовательных независимых бросках монеты с вероятностью p =0,53 (независимые события). Игрок А имеет начальный капитал X₀, и капитал может бесконечно делиться. Применяя Теорему 1 (vi), f* = p - q = 0,53 – 0,47 = 0,06, Таким образом, в каждой игре он должен ставить 6 % текущего капитала, чтобы X_n рос с максимальной скоростью и с нулевой вероятностью краха. Если Игрок А постоянно ставит меньшую долю, чем 6 %, X_n также будет расти до бесконечности, но медленнее.

Если Игрок A постоянно ставит долей большей чем 6 %, но меньше f_с , возникает то же самое. Решая уравнение g(f) = 0,53log (l +f) + 0,47log (l - f) = 0 численно на компьютере получаем fc = 0,11973 ^¯. Так, если ставка больше чем примерно 12 %, то даже при том, что Игрок А может временно наслаждаться быстрой скоростью роста, возможные колебания вниз непременно приведут величину X_n к нулю. Вычисление дает коэффициент роста g(f*)= f (0,06) = 0,001801 так, что после n последовательных ставок логарифм среднего величины капитала Игрока А будет стремиться к значению в 0,001801*n раз превышающему стартовый капитал. Приравнивая 0,001801n = log 2, получаем ожидаемое время, необходимое для удвоения капитала примерно равное n = 385.

Критерий Кэлли может легко быть расширен на игры с неравными выплатами. Предположим, Игрок А выигрывает b единиц на каждую единицу ставки. Далее предположим, что на каждой попытке вероятность победы p> 0 и pb - q> 0, так что игра выгодна для Игрока А. Методы, подобные рассмотренным, могут использоваться для максимизации

Вычисления дают f* = (bp - q)/b, оптимальную долю текущего капитала, которая должна быть поставлена в каждой игре, чтобы максимизировать коэффициент роста g (f).

Эта формула для f ^* появилась в Thorp (1984) и была предметом обсуждения в апреле 1997 в интернете на сайте Станфорда Вонга http://bj21.com. Один из обсуждавшихся там вопросов состоял в том, что можно потерять только равные по величине ставки, так что нет оснований рассматривать простое обобщение этой формулы для ситуации, когда единица ставки выигрывает b с вероятностью p> 0 и теряет a с вероятностью q. Тогда, если ожидание m ≡ bp - aq > 0, f* > 0 и f* = m/ab. Обобщение, однако, необходимо. Можно покупать в кредит на финансовых рынках и терять гораздо больше ставки. Примеры: покупка товарного фьючерса или короткая продажу (когда потеря потенциально неограничена). См., например, Thorp и Kassouf (1967).

Педанты, которые настаивают, что эти выплаты не биноминальны, могут рассмотреть короткую продажу способом двоичных чисел. Эти способы описаны у Browne (1996).

Критика, иногда звучащая в адрес стратегии Kelly – то, что капитал на самом деле не делится бесконечно. В реальном мире, ставки - умноженные минимальные единицы, типа 1 $ или 0,01 $. На рынках ценных бумаг, где система учета компьютеризованна, минимальная единица может быть сколь угодно малой. С учетом минимально позволенной ставки "крах" в обычном смысле возможен всегда. Не трудно показать, однако, (см. Thorp и Waiden, 1966) что, если минимальная позволенная ставка невелика относительно начального капитала игрока, то, вероятность краха в обычном смысле незначительна, а также то, что теория, описанная здесь, является полезной аппроксимацией. Этот раздел написан согласно работе Rotando and Thorp (1992).

Оптимальный рост: формулы критерия Келли для практиков

Поскольку критерий Келли асимптотически максимизирует ожидаемую норму роста капитала, он часто называется стратегией оптимального роста. Интересно сравнить его с другими стратегиями фиксированных долей. Я представлю некоторые результаты, которые нахожу полезными для практики. Я хочу постараться объяснить все это просто и понятно. Эти результаты появились после размышлений об "интересных вопросах". Я не делал полную литературную выборку, но я знаю, что похожие результаты были уже представлены математической общественности. См. например. Browne (1995, 1996) и дальнейшие ссылки.

(a) Вероятность достижения установленной цели за n попыток.

Сначала рассмотрим подбрасывание монеты. Мы начнем с изложения связанных с нашей задачей особенностей стандартного Броуновского движения. Howard Tucker обратил на них мое внимание еще в 1974 году, и это, вероятно, наиболее полезный отдельный факт из всех, что я знаю, имея дело с разнообразными проблемами азартных игр и с теорией производных финансовых инструментов. Для стандартного Броуновского движения X (t) мы имеем

где α = а√Т, а β = b/√T. См. Рисунок 2 и Приложение 2, где дан вывод формулы (3.1)

В нашем случае а < 0, b > 0, так что lim_T→∞ P(X(t) ≥ at + b, 0 ≤ t ≤ T)=1.

Пусть f будет долей ставки. Пусть Y_i, i=1..., n,– независимые тождественно распределенные (i.d.d..) величины. P (Y_i=1)=p > 1/2, P (Y_i =-1)=q < 1/2; пусть также p < 1, во избежание тривиального случая p= 1.

Ставим фиксированную долю ставки f, 0 < f < 1, в каждой попытке. Пусть V_k будет величина капитала игрока или инвестора через k попыток, при начальном значении V₀. Выберем Vo= 1 (без потери общности); число попыток n; цель С > 1.

Какова вероятность того, что V_k ≥ С для некоторого k, 1 ≤ k ≤ n? Она та же самая, как вероятность, что log V_k; ≥ log C для некоторого k, 1 ≤ k ≤ n. Обозначая ln=log_e, имеем:

Сдвиг за n попыток: nm

тогда и только тогда, когда:

Дисперсия за n попыток: s²n

где

, или, равносильно:

Мы хотим найти вероятность Рrob(S_k ≥ ln C - mk, 1 ≤ k ≤ n).

Для этого мы используем нашу формулу Броуновского движения, чтобы аппроксимировать S_n через Prob (X(t) ≥ lnС - Хt/s², 1 ≤ t ≤ s²n) где каждое значение S_n приближено равно X(t) со сдвигом 0 и дисперсией s² (0 ≤ t ≤ s², s² ≤ t ≤ 2s²..., (n - 1)s² ≤ t ≤ ns²). Замечание: приближение "хорошо" только для "больших" n.

Тогда в формуле (3.1):

Пример 3.1

Откуда P(·)=0.9142

Пример 3.2

Повторим решение Примера 3.1 при

f =0.02;

тогда m =0.000200013

s² =0.000399947,

и P(∙) =0.9214

(b) Вероятность того, что капитал когда-либо уменьшится до доли x от начальной величины

Это вопрос, который причиняет много волнений игрокам и инвесторам. На него легко можно ответить, хотя бы и приблизительно, используя наши предыдущие методы.

Используя обозначения предыдущего раздела, мы хотим найти P (V_k ≤ x для некоторых k, 1 ≤ k ≤ ∞). Сходные с этими методы выдают (намного проще) формулу непрерывного приближения:

Prob (·)=e^2ab, где a =- m/s², а b=- ln x, что можно записать, как

(3.2) Prob (·)= x^(2m/s²), где ^ означает возведение в степень.

Пример 3.3.

p=0.51 f=f* =0.02

2m/s²=1.0002

Prob(·) =x

Мы увидим в разделе 7, что для ограниченного непрерывного приближения и оптимальной доли Келли f*, Р (V_k (f *) ≤ x для некоторых k ≥ 1)=x.

Мой опыт показывает, что большинство осторожных игроков или инвесторов, которые используют Келли, находят частоту существенного сокращения капитала неудобно большой. Теперь мы видим почему. Чтобы уменьшить ее, они предпочитают ставить несколько меньше, чем рекомендуемая доля ставки f*. Это также повышает уровень безопасности в случае, если игровые ситуации менее благоприятны, чем ожидалось. Потери из-за уменьшенном роста капитала не является серьезными для умеренной «недоставки». Мы обсудим это позже, в разделе 7.

(с) Вероятность попадания в или выше указанной величины
в конце определенного числа попыток.

Доктор Richard Hecht (1995) предложил взять эту вероятность в качестве цели и использовал для этого численный метод определения оптимальной (в соответствии с этим критерием) фиксированной доли для p - q= 0.02 и различных с, n и определенных вероятностей успеха.

Это - намного более легкая задача, чем похожая на нее (a). Для вероятности того, что X(T) в конце концов превысит цель, мы получаем:

где и = x/√T так что x=aT +b дает u√T = aT + b и U=aT^1/2-bT^-1/2. Интеграл равен

Для Примера (3.1): f =0.0117 и P=0.7947. Для Примера (3.2): P=0.7433. Пример (3.1) - для оптимальной доли Хечта, а Пример (3.2) - для оптимальной доли Кэлли, Обратите внимание на различие значений P.

Наши числовые результаты соответствуют моделированию Хечта в проверенных нами случаях.

Браун (1996) дал изящное решение проблемы в непрерывном приближении: какая стратегия максимизирует вероятность достижения установленной цели С к или до указанного времени n и какова соответствующая вероятность успеха? Обратите внимание, что, в общем случае, оптимальная стратегия будет включать механизм изменения доли ставки в зависимости от оставшегося времени и расстояния до цели.

Рассмотрим пример предельного случая, когда n=1, а C=2. Если X₀<1, то никакая стратегия не сработает и вероятность успеха равна 0. Но, если 1 ≤ X₀ ≤ 2, нужно делать ставку по крайней мере 2 - X₀, таким образом любую долю f ≥ (2 — X₀)/X₀, для вероятности успеха p. В другом предельном случае: n=10, С= 2¹⁰ =1024, X₀=1. Здесь единственная стратегия, которая может преуспеть, состоит в том, чтобы делать ставку f=1 в каждой попытке. Вероятность успеха равна p¹⁰ для этой стратегии и 0 для всех других (если p < 1), включая Келли.

(d) Непрерывная аппроксимация времени, ожидаемого для достижения цели.

Согласно Теореме l (v), стратегия оптимального роста асимптотически минимизирует ожидаемое время достижения цели. Вот что это означает. Предположим для цели С, что m(C) – наибольшее значение нижней границы для ожидаемого времени достижения C из всех стратегий. Предположим, t*(C) - ожидаемое время при использовании стратегии Келли. Тогда lim_C→∞ (t*(c)/m(c))= 1.

Непрерывное приближение к ожидаемому числу попыток для достижения цели C>X₀=1 будет

(3.4) n(C,f)=(lnC)/g(f)

где f - любая стратегия фиксированной доли. В Приложении 3 дан вывод этих формул. Теперь, т.к. g(f) имеет единственный максимум g(f*), то и n(C, f) имеет единственный минимум на f=f*. Кроме того, мы можем увидеть, насколько дольше, в среднем, придется добираться до С при отклонении от f*.

(e) Сравнение стратегий с фиксированной долей: вероятность, что одна стратегия опередит другую после n попыток.

Теорема 1 (iv) гласит, что капитал при использовании стратегии Келли будет стремиться, в конечном счете, к бесконечно большому приумножению капитала, чем использовании любой "существенно иной" стратегии. Можно показать, что любое фиксированное f ≠ f* - это "существенно иная" стратегия. Это приводит нас к вопросу о том, насколько стратегия Келли опережает другую стратегии фиксированной доли, и шире говоря, насколько быстро одна стратегия фиксированной доли опережает другую (или отстает от другой).

Если W_n - число побед за n попыток, а n — W_n - число проигрышей, то

G(f)=(W_n/n) ln (l + f) + (1 - W_n/n) ln (1 - f)

это фактически (случайная переменная) коэффициент роста.

Как мы видели, его ожидание

(3.5) g(f)=E(G(f))=p log(1 + f) + qlog(1 - f)

а дисперсия G(f) -

и из этого следует, что G(f), который представиться как G(f)=a(∑T_k)/n+b, приблизительно нормально распределено со средней g(f) и дисперсией VarG(f). Это позволяет нам получить распределение X_n и еще раз ответить на вопрос заданный в 3(c). Проиллюстрируем это на примере.

Пример 3.3 p=0.51 q=0.49 f*=0.02 N=10,000 и

s= стандартное отклонение G(f)

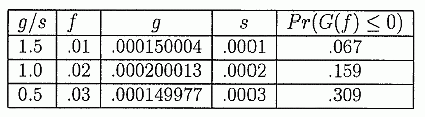
Далее находим распределение G(f₂) - G(f₁). Мы рассматриваем два случая.

Случай 1. Одна и та же игра.

Здесь мы предполагаем, что оба игрока делают ставки на одни и те же попытки, например, на монету, или на одинаковые сдачи в блэк джеке, или на одно и тот же исход на тотализаторе. На рынке акций, оба игрока могут вкладывать в одну и ту же бумагу одновременно, например, инвестирую в индексный фонд S&P 500.

Мы находим

где G(f₂) — G(f₁) приблизительно нормально распределено с этими средним и дисперсией.

12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: