 |
Модели математического состояния
|
|
|
|
I. «Вход – Выход»
 |
Вход Выход
Это математическое выражение связывает выходные координаты с входным воздействием при изменении координат
Эта модель не совсем нас удовлетворяет, т.к. не определяет состояние системы в каждый момент времени, а так же положение.
II. «Вход-Состояние-Выход»
|
Вход Выход
На практике используются редко.
I. «Вход-Выход»
Дано: ТВД с ВИШ (турбовинтовой двигатель с видоизменяющимся шагом)
Требуется: ММ САУ скорости вращения вала двигателя?
z – координата угла поворота лопасти винта
w - угловая скорость вращения двигателя
y – характеристика работы топливной системы
wзад – обороты дигателя
ЧЭ – чувствительный элемент, сравнивающий wзад и w
> - усилительный блок
ИМ – исполнительный механизм (поворачивает ОУ)
ОУ – двигатель
В паспорте двигателя задаются 2 характеристики:
А – Механическая характеристика двигателя (зависимость момента двигателя от w;
Б – Нагрузочня характеристика двигателя (характеризует то, какую нагрузку испытывает двигатель во время работы).
Условие Дирихле
Запишем поэлементно уравнения
1. ММ ОУ
Рассматривается только ОУ
2. Хвых = w
z=jл=Хвх - управляющее воздействие – поворот полости винта или возмущение f(t)
3. Возможны 2 варианта:
а) За начало координат берется начальное состоя ние объекта. В этом случае получаем неоднородные д.у.
|
переходный процесс
б) За начало координат принимается конечное (новое) состояние объекта. В этом случае получаем однородные д.у., но с ненулевыми начальными условиями.
4. Уравнение статики – уравнение баланса, равновесия, когда Мд = Мс.
|
|
|
Найдем эту точку на характеристиках А и Б.
Это рабочая точка, когда wзад = w0, у0 = const, φло = const = z0.
5. Приращение координат при наличии возмущений.
xi = xi0 + Δx; Fi = Fi0 + ΔF
w = w0 + Dw
Мд = Мд0 + DМд0
Мс = Мс0 + DМс0
ММО: DМд(w,t)
DМc(w,jл,t)
Предположим, что D «малые».
6. I – момент инерции вращающихся частей
Уравнение динамики с учетом малых приращений.
7. Уравнение ММ динамического состояния «в отклонениях» (вариациях)
Необходимо проверить условие Дирихле.
8. Линеаризация
Линеаризованное динамическое уравнение «в отклонениях»
|
,
где 
и 
- паспортные величины
- ММ ОУ (в относительных единицах)
Физический смысл коэффициентов
- машинная потоянная времени – характеризует быстродействие ОУ – время, за которое двигатель раскрутится от 0 до wн при прямолинейной раскрутке при Мн
- коэффициент самоврвнивания («вантка-встанька») – характеризует способность объекта восстанавливать свое первоначальное положение.
, где 
Избыток момента идет на увеличение скорости.
Такой объект устойчивый, если
|
Для маневренных самолетов необходима неустойчивая СУ (так легче управлять)
- коэффициент регулятора – определяет силу управляющего воздействия и эффективность этого влияния.
Полученное уравнение определяет свойства системы, а не состояние.
Чтобы найти уравнение переходного процесса, надо решить это уравнение.
По аналогии получаются ММ других объектов системы.
Задача
Дано: Tj, Kc, Km = 0, j(0)= j0, f(t) = 1[t]
Требуется: j(t) =?, ур-ие переходного процесса.
Решение: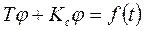 
1. Свободная 2. Вынужденная
т.е. j(t)= j (t)св + j (t)в
T = Tj/Kc
Математическая модель САУ
 |
Приведем «в порядок» и запишем в операторной форме:
|
|
|
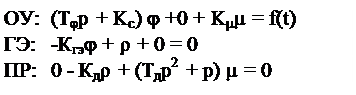
Как изменятся выходные координаты при воздействии?
|
|
Решаем систему уравнений относительно исходных координат.
Результат должен быть вида:
Решение уравнений динамического состояния САУ
Методы Решешения:
1. Операторный (не будем использовать)
2. Преобразование Фурье
- оригинал
- изображение функции по Фурье
Ограничения (чтобы функцию разложить по Фурье должны быть:
а. Нулевые граничные условия
б. Условия Дирихле
(когда известно, что функции близки к гармоническим)
3. Преобразования Лапласа
F(s) – изображение
f(t) – оригинал
F(s) ¸ f(t)
Особенности:
1. Начальные условия любые.
2. Сложные правые части.
3. Не выполнение условий Дирихле. Например: 1[t], sin(wt)…
Преобразования Лапласа позволяют:
1. Получать аналитические решения.
2. Широко использовать опыт (справочники, таблицы, …)
3. Решать конечные задачи (когда не интересует промежуточные решения)
4. Решать задачи анализа и синтеза и т.д. и т.п.
Основные свойства:
|
Оператор
Комплексная переменная 
Имеем ММ в виде системы линейных уравнений. Преобразуем все функции по Лапласу в этом сценарии:
|
|
|
|
|
