 |
Определение реакции на воздействие произвольного типа
|
|
|
|


|

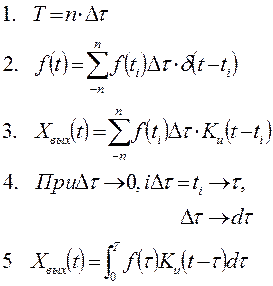
 |
ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
|
 | |||
 | |||
= Аsinwt = B(w)sin[wt+φ(ω)]

А =const
АЧХ ω = var
 | |||
| |||
ФЧХ
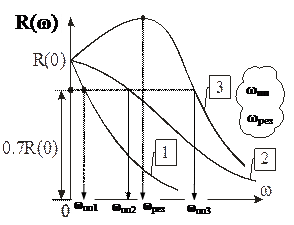
Чем шире полоса пропускания, тем tпп меньше
wпп – полоса пропускания
wрез – резонансная частота

Объединение характеристик на комплексной плоскости



Предположим, дано уравнение в операторной форме
D(p) ×Xвых = M(p) ×Хвх
Пусть: Хвх = Аsinwt = J m A×ejωt
Тогда: Хвых = B(w)sinwt[wt+φ(ω)] = J m B(w)×ej[wt+φ(ω)]
Преобразования Фурье
p = jw
 | |||
 | |||
т.е. D(jw)×B(w)×ejωt ×ej φ(ω) = M(jw)×A×ejωt
 | |||
 | |||




Основные свойства АФЧХ
1. 
2. Частотная характеристика есть функция комплексного переменного


|




3. Обратная ЧХ (иногда удобна)
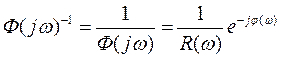
4. Интеграл Фурье
 |


5. Пусть есть передаточная функция
|
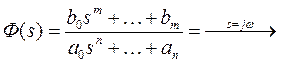
|

 б)
б) 

Фазовые сдвиги всегда меньше, если все нули левые => минимально фазовая система (МФС)
Все ЧХ находятся в однозначной зависимости в МФС
 МФ САУ R(ω) ¸ φ (ω)
МФ САУ R(ω) ¸ φ (ω)

P(ω) ¸ Q(ω)
6. ЧХ для отрицательного диапазона частот – зеркальное отображение для положительного диапазона частот

7. Условие физической реализуемости


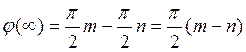
Если система статичная, то ЧХ должна начинаться из нуля

Если система астатичная, то ЧХ начинается из бесконечности

8. ЧХ группы соединенных элементов
|
|
|


 |
ВЕКТОР!!! Речь идет именно о векторах.
U(w) – действительная частотная характеристика САУ в разомкнутом состоянии
P(w) – действительная частотная характеристика САУ в замкнутом состоянии
V(w) – мнимая частотная характеристика САУ в разомкнутом состоянии




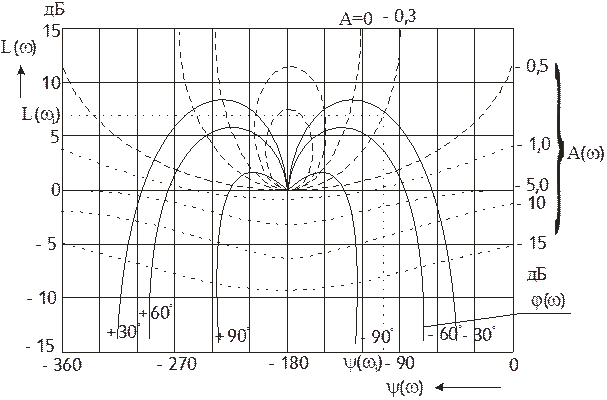
ЛОГАРИФМИЧЕСКИЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
 | |||
| |||


| |||
 |
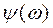
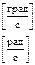
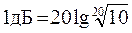



Изменение частоты в 2 раза - октава










wсопр – частота сопряжения
wср – частота среза
При последовательном соединении:
 |





 Динамические характеристики САУ
Динамические характеристики САУ
|
ТИПОВЫЕ ДИНАМИЧЕСКИЕ ЗВЕНЬЯ
Динамическое звено - элемент (динамический) САУ, обладающий одной степенью свободы и детектирующими свойства.
 ИДЕАЛЬНОЕ АПЕРИОДИЧЕСКОЕ
ИДЕАЛЬНОЕ АПЕРИОДИЧЕСКОЕ

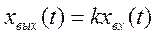

 T – постоянная времени
T – постоянная времени
 - собственная частота
- собственная частота
К- коэффициент передачи (усилия)
 |





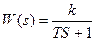
|
 | |||||
 | |||||
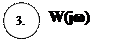 | |||||


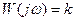

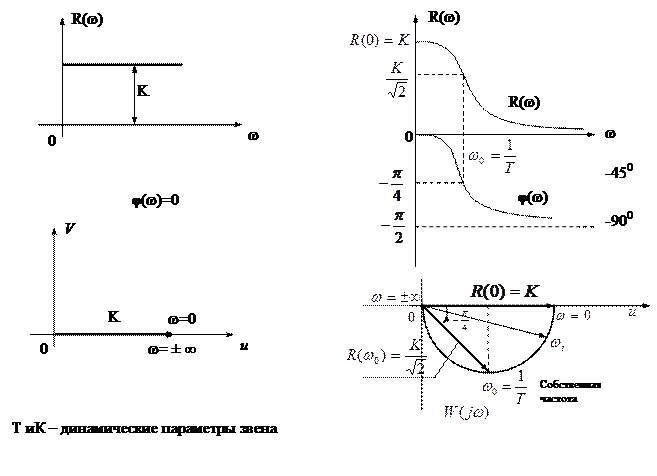 |


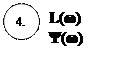 L*(w)= L (w)=20 lgK L(w)= -20 lg
L*(w)= L (w)=20 lgK L(w)= -20 lg 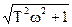
 |
Низкочастотный участок 1>>Tw LI(w)=0
|
 |



|
|
|
|
 |
Ψ(w) = -arctgTw

 | |||||||
 | |||||||
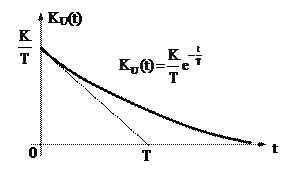 | |||||||
 |
Дифференцирующее
|
| Интегрирующее
| ||||||
  
|  
|  
| ||||||
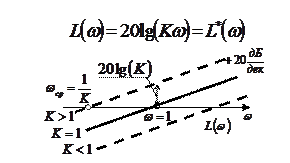
| 
| |||||||
|  

| |||||||
| 
| 
| ||||||

| 
| 
|


 КОЛЕБАТЕЛЬНОЕ
КОЛЕБАТЕЛЬНОЕ





 | |||
 |

|
|
|
 |


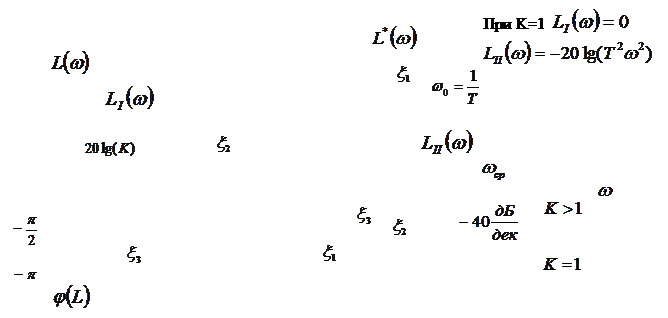
 |
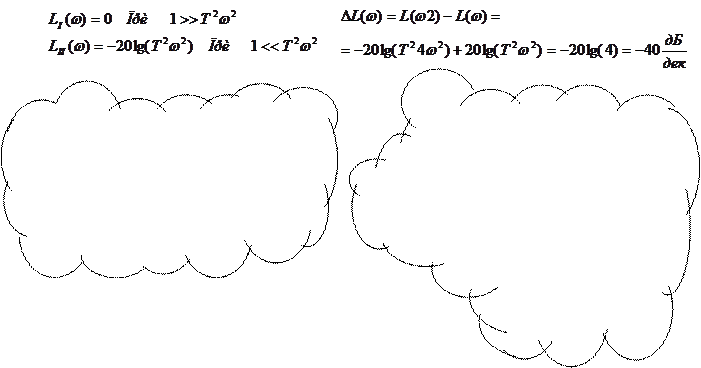


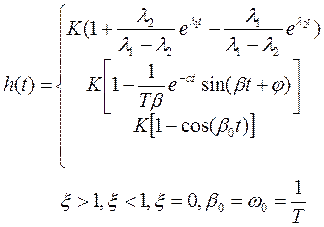
|

| |||||||||||||||||
| 
| |||||||||||||||||
Вопросы???

| Как экспериментально определить К, Т и  ?
Как изменится ?
Как изменится  колебательного звена при изменении
К, Т и колебательного звена при изменении
К, Т и  ? ?
 
| |||||||||||||||||
ПРАВИЛА структурных преобразований.
 1. 1.
 2. 2.
3.
4.
|  8.
Задачи: 8.
Задачи:
 
 
   1. 1.
| |||||||||||||||||

|
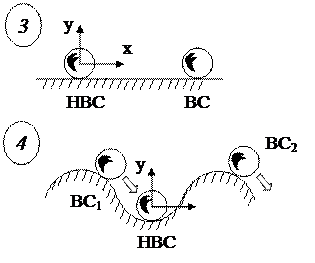
УСТОЙЧИВОСТЬ САУ
Невозмущённое
состояние
(равновесия)


| 
|
|  | ||||


А. М. Ляпунов
|

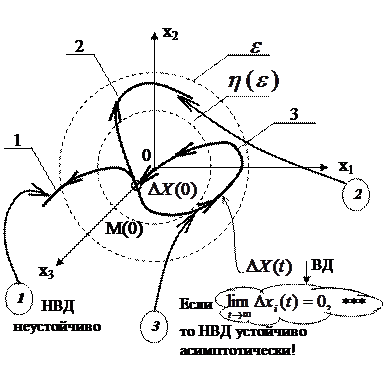
НВД 


 НВД устойчиво по отношению к переменной xi, если при всяком
НВД устойчиво по отношению к переменной xi, если при всяком 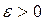 , как бы мало оно ни было, можно найти другое
, как бы мало оно ни было, можно найти другое  такое, что для всех
такое, что для всех  удовлетворяющих при
удовлетворяющих при  условию
условию  *, возмущенное движение при t>0 будет удовлетворять неравенству
*, возмущенное движение при t>0 будет удовлетворять неравенству 
 - область
- область 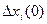
 - область допустимых отклонений.
- область допустимых отклонений.
Выводы:
- Об устойчивости НВД судят по характеру
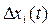 .
. -
 .
. - Условия ** накладываются при
 .
. - В общем случае не требуется ***, достаточно **.
- Устойчивость по Ляпунову, это устойчивость в “малом”.
- Определение носит качественный характер.
- Механический смысл определе-ния устойчивости в характерис-тике прочности и сопротивляемости действующим возмущениям.
| |||
I. Метод исследования Ляпунова:
Отыскание общего или частного решений уравнений ВД - исследование
ние линеа-ризованных уравнений (уравнений первого приближения)
Основан на поиске и свойствах специальных функций Ляпунова.
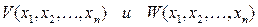
где 
|
|
|



 , то характеристическое уравнение,
, то характеристическое уравнение, 
 (при k = 1)
(при k = 1)
 =wсопр
=wсопр

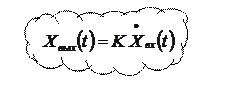



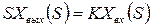










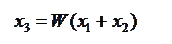


 7.
7.


 2.
2. 3.
3.
 4.
4.



