Исследование устойчивости НВД по уравнениям первого приближения.

(Первая метода А.М. Ляпунова)

 

Дано: диф. уравнение линеариз. САУ

корни XY

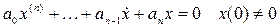
Уравнение ВД:

где - корни

Если - “левые”, т.е. ,

Условие АСУ условию

то

Вывод:

 

АСУ – асимптотическая устойчивость

 

Выводы:

 

 

 

 

Теоремы А.М. Ляпунова

Теорема 1. Если все ХУПП (характеристическое уравнение первого приближения) имеют , то НВД АСУ независимо от вида отброшенных при линеаризации нелинейных членов (высших членов ряда Тейлора) разложения.

Теорема 2. Если среди ХУПП есть хотя бы один с , то НВД НУ…

Теорема 3. Критический случай.

Если среди ХУПП есть хотя бы один с , то для исследования ус-сти

 

 

НВД следует использовать исходные нелинейные уравнения, т.е. устойчивость зависит и от вида отброшенных при линеаризации членов разложения порядка выше первого.

Прямая метода А.М. Ляпунова.

	[1] стр. 65-73

 

Теоремы А.М. Ляпунова позволяют сделать вывод, при каких условиях заключения об устойчивости, полученные для линеаризованной системы, сохраняют силу и для исходной нелинейной САУ.

 

Анализ устойчивости САУ с учетом запаздывания

 

Звено запаздывания

Хвх? Хвых

 

Запаздывание –явление, когда звено реагирует только через время t после подачи команды

ПФРСАУ

 

t

 

Аппериодическое звено:

Хвх 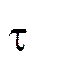Хвых

Хвых(s)=W(s) Хвх(s)

 

Если брать по времени, подав на вход ступенчатое воздействие, то на выходе будет экспонента, сдвинутая на τ относительно нуля.

 

 

 

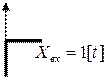Соберем все в одну систему с учетом запаздывания

 

g(t) W1 W2 W3 W4 Xвых

 

 

Если бы не было запаздывания

 

Сиситема без запаздывания называется предельной

С учетом запаздывания

 

 

При каждом значении ω появляется дополнительный сдвиг по фазе, равный ωt.

 

Системы с запаздыванием не являются минимально фазовыми

 

Запаздывание вызывает уменьшение устойчивости системы.

Проверим это с помощью критерия устойчивости:

“левые”

Трансцендентное уравнение

 

Какой же критерий Найквиста отражен здесь?

 

 

 

 

Каждый вектор ЧХ с учетом запаздывания, оставаясь по модулю тем же, будет поворачиваться на угол ωτ

 

Запаздывание может «съесть» запасы устойчивости

Поэтому нужно найти допустимое значение запаздывания – критическое запаздывание – такое запаздывание, при котором система выходит за границу устойчивости.

 

Имелся запас по фазе γ

 

 

 

Если γ = 0, то система находится на границе устойчивости

 

 

Если:

1. t<t_кр - система остается устойчивой при наличии запаздывания

2. t=t_кр - система на границе устойчивости

3. t>t_кр – система неустойчива

Метод “D-разбиения”

(Метод Нейморка)

 

 

о

о

о

о

 

 

Имеется n-мерное пространство.

По каждому измерению этого пространства будем откладывать коэффициент характеристического уравнения и образуем «пространство коэффициентов характеристического уравнения».

Каждая точка в этом n-мерном пространстве будет соответствовать своему характеристическому уравнению.

 

Предположим, что во всех точках в этой области, все корни х и у будут левыми. Эта область – область устойчивости в пространстве коэффициентов уравнения.

Этих областей может быть несколько.

 

Определим границы областей устойчивости:

Все пространство разбиваем на отдельные области и из этих областей какие-то являются устойчивыми

 

Условие границы S = jω

Дано:

- уравнение границы “D”

 

D(n) – область устойчивости (все корни «левые»)

 

⇐ Предыдущая1234

Поделиться:

Воспользуйтесь поиском по сайту: