 |
Обозначения физических величин
|
|
|
|
Раздел«Теоретическаямеханика»
m – масса;
F (F x, F y, F z) – сила (составляющие силы по координатным осям);
М – момент силы (момент пары);
q – интенсивность распределенной нагрузки;
R (X, Y, Z) – реакция (реактивная сила);
M R – реактивный момент в жесткой заделке;
T – сила натяжения гибкой связи
(каната, троса, ремня);
F ∑ – равнодействующая сила;
М ∑ – равнодействующий момент;
F т– сила трения;
M т– момент трения; G – сила тяжести;
F и– сила инерции;
f – коэффициент трения скольжения;
А – площадь;
S x – статический момент площади относительно оси х;
V – объем;
С – центр тяжести;
W – работа силы (момента силы);
P – мощность силы (момента силы);
l (l AB) – длина (длина между точками A и В);
t – время;
s – перемещение, путь;
v – скорость;
а – ускорение;
a n (a t) – нормальное (тангенциальное) ускорение;
j – угол поворота;
w – угловая скорость; рад/с e – угловое ускорение;
n – частота вращения вала, об/мин;
P – мощность;
h – коэффициент полезного действия (КПД).
Раздел «Сопротивление материалов»
[s] – допускаемое нормальное напряжение (общее обозначение); [sр] – то же, при растяжении;
[sс] – то же, при сжатии; [sсм] – то же, при смятии; sВ – предел прочности;
sВр (sВс)– предел прочности при растяжении (при сжатии);
sт – предел текучести;
smax (tmax) – наибольшее напряжение в поперечном сечении бруса; sпц – предел пропорциональности;
[t] – допускаемое касательное напряжение; [tкр] – допускаемое напряжение при кручении;
[tср] – то же, при срезе;
j – угол закручивания бруса при кручении;
[j0] – допускаемый относительный угол закручивания;
Е – модуль продольной упругости;
J x, J y – главные центральные моменты инерции;
J p – полярный момент инерции;
|
|
|
М х – изгибающий момент в поперечном сечении бруса относительно оси х; М изг – изгибающий момент, суммарный для бруса круглого поперечного сечения;
М кр – крутящийся момент в поперечном сечении бруса;
N – продольная сила в поперечном сечении бруса;
s [ s ] – коэффициент запаса прочности (нормативный);
Q y, Q – поперечная сила, действующая вдоль оси у или суммарная.
Задания для контрольной работы
Задача №1
Определить аналитическим и графическим способами усилия в стержнях АВ и ВС заданной стержневой системы (рис. 1.1). Исходные данные для задачи своего варианта взять из таблицы 1.
Таблица 1
| № варианта | № схемы | F1, кН | F2, кН | α1, град. | α2, град. | α3, град. |
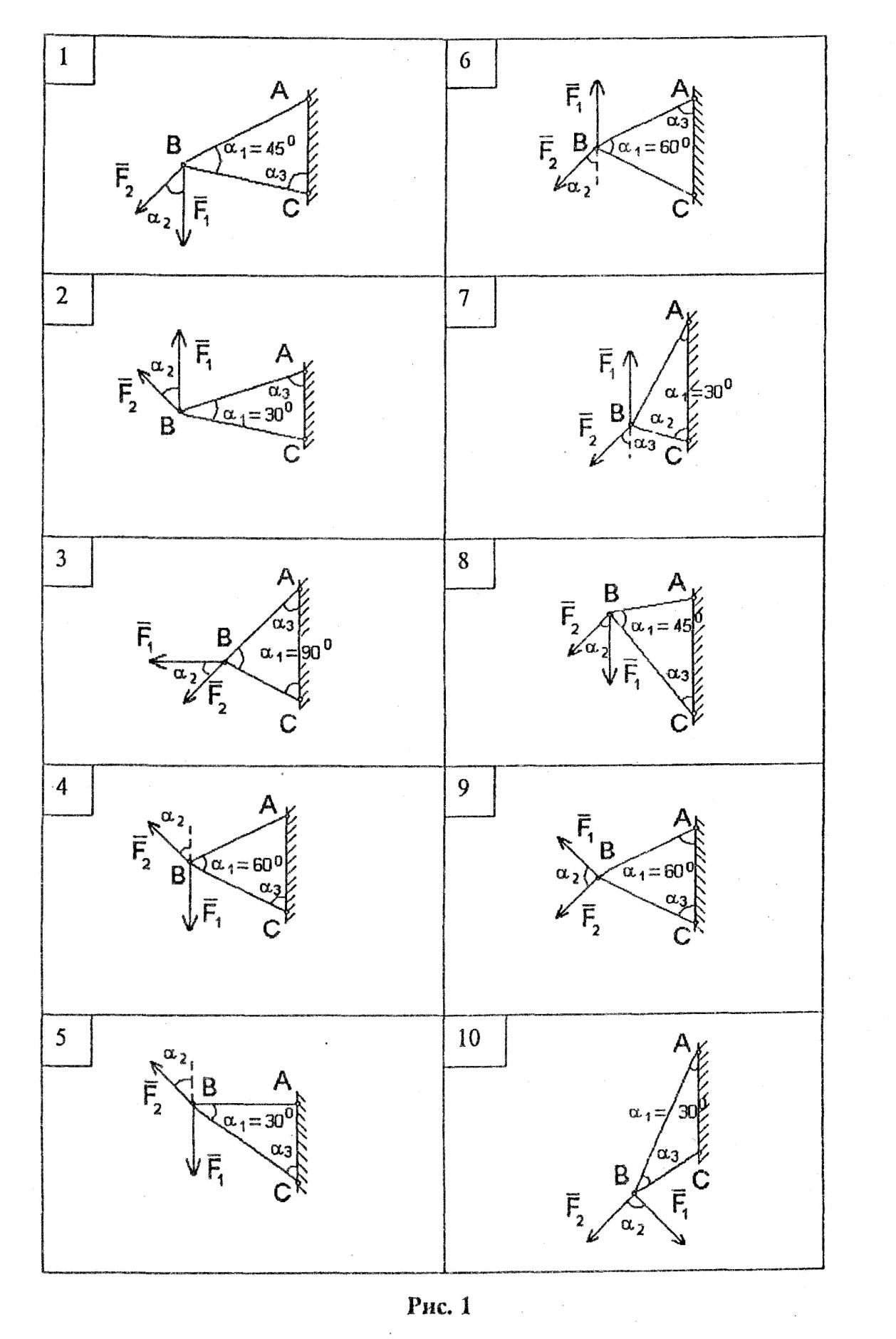
Рис. 1.1
Пример решения задачи №1. Определить реакции стержней, удерживающих грузы F1=70 кН и F2=100 кН (рис 1.2,а). Массой стержней пренебречь.
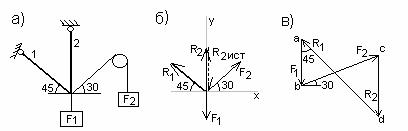
Рис.1.2
Указание. В данной задаче рассматривается равновесие плоской системы сходящихся сил и требуется определить реакции двух шарнирно соединенных между собой стержней, удерживающих два груза. Таким образом, к шарниру В в каждой задаче приложены четыре силы, из которых две неизвестны. Для задач такого типа универсальным является аналитический метод решения.
Последовательность решения задачи:
1. выбрать тело (точку), равновесие которого следует рассматривать;
2. освободить тело (шарнир В) от связей и изобразить действующие на него активные силы и реакции отброшенных связей. Причем реакции стержней следует направить от шарнира В, так как принять считать предположительно стержни растянутыми;
|
|
|
3. выбрать систему координат, совместив ее начало с точкой В, и составить уравнения равновесия, используя условия равновесия системы сходящихся сил на плоскости 
;
4. определить реакции стержней из решения указанной системы уравнений;
5. проверить правильность полученных результатов по уравнению, которое не использовалось при решении задачи, либо решить задачу графически.
Решение.
1. Рассматриваем равновесие шарнира В (рис 1.2,а)
2. Освобождаем шарнир В от связей и изображаем действующие на него активные силы и реакции связей (рис.1.2,б)
3. Выбираем систему координат и составляем уравнения равновесия для системы сил, действующих на шарнир В.
4. Определяем реакции стержней R 1 и R 2, решая уравнения. Из уравнения 1:
Подставляем найденное значение R 1 в уравнение 2 и получаем
Знак минус перед значением R 2 указывает на то, что первоначально выбранное направление реакции неверно – следует направить реакцию R 2 в противоположную сторону, т.е. к шарниру В (на рис.1.2,б истинное направление реакции R 2 показано штриховым вектором)
5. Проверяем правильность полученных результатов, решая задачу графически (рис. 1.2,в). Полученная система сил (рис.1.2,б) находится в равновесии, следовательно, силовой многоугольник, построенный для этой системы сил, должен быть замкнутым.
Строим силовой многоугольник в следующем порядке (рис.1.2,в): в выбранном масштабе (например, 
=2 кН/мм) откладываем заданную силу F 1 (ab = F 1), затем из точки b под углом 300 к горизонту откладываем силу F 2(bc = F 2), далее из точек а и с проводим прямые, параллельные положениям стержней 1 и 2. Эти прямые пересекаются в точке d и в результате построения образуется замкнутый многоугольник abcd, в котором сторона cd=R 2, а сторона da = R 1. Измерив длины этих сторон (в мм) и умножив на масштаб построения 
, получаем значения реакций стержней: 
Графическое решение подтверждает правильность первого решения.
Задача № 2
Определить опорные реакции балки (рис.2.1), лежащей на двух опорах. Данные своего варианта взять из таблицы 2.
Таблица 2
|
| М |
| F |
| a1 |
| a2 |
| a3 |
Рис.2.1
Пример решения задачи №2. Определить реакции опор балки (рис.2.2, а).
Рис.2.2
Указание. Во всех данных задачах требуется определить реакции опор балок. Учащимся необходимо приобрести навыки определения реакций опор, так как с этого начинается решение многих задач по сопротивлению материалов и деталям машин.
Последовательность решения задачи:
1. изобразить балку вместе с нагрузками;
2. выбрать расположение координатных осей, совместив ось х с балкой, а ось y направив перпендикулярно оси х;
3. произвести необходимые преобразования заданных активных сил: силу, наклоненную к оси балки под углом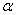 
, заменить двумя взаимно перпендикулярными составляющими, а равномерно распределенную по закону прямоугольника нагрузку – ее равнодействующей, приложенной к середине участка распределения нагрузки;
4. освободить балку от опор, заменив их действие реакциями опор, направленными вдоль выбранных осей координат;
5. составить уравнения равновесия статики для произвольной плоской системы сил таким образом и в такой последовательности, чтобы решением каждого из этих уравнений было определение одной из неизвестных реакций опор;
6. проверить правильность найденных опорных реакций по уравнению, которое не было использовано для решения задачи.
Решение.
1.Изобразим балку с действующими на нее нагрузками (рис.2.2,а)
2. Изобразим оси координат x и y
3.Силу F заменяем ее составляющим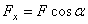и 
и 
. Равнодействующая qСD равномерно распределенной нагрузки, приложенная в точке пересечения диагоналей прямоугольника (рис.2.2,б), переносится по линии своего действия в середину участка CD, в точку К.
4. Освобождаем балку от опор, заменив их опорными реакциями (рис.2.2,в)
5. Составляем уравнения равновесия статики и определяем неизвестные реакции опор.
|
|
|
a) Из уравнения моментов всех действующих на балку сил, составленного относительно одной из точек опор, сразу определяем одну из неизвестных вертикальных реакций:
кН
b) Определяем другую вертикальную реакцию:
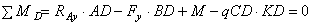
кН
c) Определяем горизонтальную реакцию:
; 
кН
6. Проверяем правильность найденных результатов:
.
Условие равновесия 
выполняется, следовательно, реакции опор найдены верно.
Задача №3
Построить графики пути, скорости и ускорения точки, движущейся прямолинейно согласно закону для первых пяти секунд движения. Данные для своего варианта взять из таблицы.
Таблица 3
| Вариант | Уравнение движения точки |
| S= 20t-5t2 | |
| S= 20t-4t2 | |
| S= 20t-3t2 | |
| S= 20t-2t2 | |
| S= 19t-5t2 | |
| S= 19t-4t2 | |
| S= 19t-3t2 | |
| S= 19t-2t2 | |
| S= 18t-5t2 | |
| S= 18t-4t2 |
|
|
|
