По выполнению задачи №4 раздела «Сопротивление материалов»

Приступая к решению задачи раздела «Сопротивление материалов», в котором изучаются способы расчета деталей и конструкций на прочность и жесткость, необходимо повторить из раздела «Статика» методику определения реакций связей и способ определения положения координат центра тяжести плоских сечений.

Изучив соответствующий учебный материал, следует особое внимание обратить на метод сечений для определения внутренних силовых факторов (ВСФ), которые являются причиной потери прочности.

Легко запомнить все пункты метода сечений, если записать их словом «РОЗУ».

Каждая буква этого слова означает содержание определенной операции этого метода:

Р - разрезаем тело плоскостью на две части;

О - отбрасываем одну часть;

3 - заменяем действие отброшенной части внутренними силами;

У - уравновешиваем оставшуюся часть и из уравнения равновесия определяем внутренние силы.

В общем случае нагружения тела внутренние силы, возникающие в поперечном сечении нагруженного бруса, могут быть заменены их статическими эквивалентами - главным вектором и главным моментом. Если последние разложить по осям координат (рис. 4.1), то получим шесть составляющих с общим названием «внутренние силовые факторы»:

N - продольная сила;

Q_x, Q_y - поперечные силы;

Т_к - крутящий момент;

М_их, М_иу - изгибающие моменты.

Виды ВСФ N - продольная сила Q - поперечная сила Ми - изгибающий момент Тк - крутящий момент

Вид нагружения	Внутренние силовые факторы (ВСФ)	Распределение напряжений по поперечному сечению
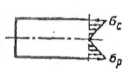
Растяжение   Сжатие
Кручение
Изгиб

 

Рис. 4.1

 

	Геометрическая характеристика прочности сечения (ГХП)	Расчетное напряжение, равное ВСФ/ГХП	Условие прочности
Любая точка сечения	Площадь А
Любая точка контура сечения	Полярный момент сопротивления Wp
Точки контура сечения, максимально удаленные от нейтральной оси	Осевой момент сопротивления W

 

Шесть внутренних силовых факторов вместе с внешними силами (к внешним силам относятся как активные, так и реактив­ные) на оставшейся части бруса образуют уравновешенную сис­тему сил, для которой можно составить шесть уравнений равнове­сия. В каждое из этих уравнений входит один из неизвестных внутренних силовых факторов. Решая уравнения, найдем:

 

 

По виду ВСФ устанавливают вид напряжения, возникающе­го в точках.

Нормальное напряжение а - следствие возникновения про­дольной силы N или изгибающих моментов М _их и М _иу; касатель­ные напряжения т - следствие возникновения поперечных сил Q _x и Q _y или крутящего момента Т _к.

Величина напряжения в поперечных сечениях тела зависит не только от величины силовых факторов, но и от размеров попе­речного сечения - от соответствующей геометрической характе­ристики прочности сечения.

Условием прочности при расчете по допускаемому напря­жению называется неравенство вида а σ ≤ [σ] или τ ≤ [τ], где [σ] и [τ] - допускаемые напряжения, т.е. максимальные значения на­пряжений, при которых гарантируется прочность детали:

 

где σ_пред - предельное напряжение для материала рассчиты­ваемой детали;

[ n ] - допускаемый коэффициент запаса прочности детали, зависит от ответственности детали, срока службы, точности рас­чета и других факторов.

В конструкциях всегда имеются элементы, ра­ботающие на растяжение или сжатие (иногда попеременно растя­жение-сжатие).

Формы и размеры этих элементов конструкций определяют­ся необходимостью обеспечить их прочность при действии растя­гивающих или сжимающих усилий, возникающих в процессе ра­боты подвижного состава.

Растяжением (сжатием) называют такое нагружение бруса, при котором в поперечных сечениях возникает только один внут­ренний силовой фактор - продольная сила N.

Продольную силу определяем при помощи метода сечений.

Продольная сила N в любом поперечном сечении бруса чис­ленно равна алгебраической сумме внешних сил, действующих на оставшуюся часть бруса:

Правило знаков: условимся внешние силы, растягивающие брус, считать положительными, а сжимающими его - отрицатель­ными.

По известной продольной силе N и площади поперечного сечения А можно определить напряжения в этом сечении:

Удлинение (укорочение) бруса или отдельных его участков определяется по формуле Гука:

Условие прочности при растяжении и сжатии имеет вид:

где σ, N - соответственно нормальное напряжение и про­дольная сила в опасном сечении (т.е. в сечении, где возникают наибольшие напряжения);

А - площадь поперечного сечения;

[σ] - допускаемое напряжение, т.е. максимальные зна­чения напряжений, при которых гарантируется прочность детали. Исходя из условия прочности, можно решать три вида задач:

1) проверка прочности;

2) подбор сечения

3) определение допускаемой нагрузки [ N ] ≤ [σ] • А.

 

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: