Алгебраические системы А.И. Мальцева

Оформление репрезентативной теории измерений стало возможным после введения академиком А.И. Мальцевым понятия алгебраической системы. Альфред Тарский, родоначальник репрезентативной теории измерений, совместно с американскими математиками Л. Хенкин и Д. Монк, посвятил памяти А.И.Мальцева свою книгу «Цилиндрические алгебры», предварив ее словами: «Посвящается профессору Анатолию Ивановичу Мальцеву, указавшему путь из логики в алгебру».

Алгебраической системой по А.И. Мальцеву называется объект , состоящий из трех множеств:

- произвольное множество некоторых элементов, которое называется носителем алгебраической системы,

- множество операций , определенных на множестве и ставящих в соответствие нескольким элементам множества новый элемент, который, однако, тоже принадлежит множеству ,

- множество возможных отношений , в которые могут вступать друг с другом элементы множества .

В определении алгебраической системы нигде не уточняется состав множества . Это может быть множество всех действительных чисел и тогда множество алгебраических операций включает в себя, в частности, операции сложения и умножения, но это может быть, например, и множество значений рейтинга телевизионных каналов с отношениями равенства и порядка. Отвлечение от конкретного содержания носителя позволяет применять теорию алгебраических систем в самых различных областях знаний.

Алгебраическая система, не содержащая операций, называется моделью, при отсутствии отношений система называется алгеброй.

Операция называется - арной, если для получения результата используется элементов носителя. Аналогично этому и отношение называется - арным, если в нем учувствуют элементов носителя. Тип алгебраической системы определяется как набор арностей операций и отношений .

Так, например, алгебраическая система на множестве натуральных чисел относится к типу , поскольку операции сложения и умножения и отношение строго порядка определены для каждой пары натуральных чисел. Система не является алгебраической, поскольку операция деления отнюдь не для всех натуральных чисел определяет натуральное число.

Алгебраическая система на множестве значений твердости материалов является моделью, но не алгеброй. На множестве не определены операции (нет возможности поставить эксперимент, который бы доказывал, что твердость одного образца равна сумме или произведению твердостей двух других образцов), но можно определить отношения эквивалентности (два образца одинаковы по твердости) и строго порядка (один образец тверже другого).

Для изучения соотношений между свойствами носителей, операциями и отношениями над элементами носителей вводится понятие изоморфизма алгебраических систем.

Две алгебраические системы 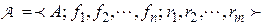и одного типа, то есть одинакового набора арностей операций и отношений, называются изоморфными, если существует взаимнооднозначное отображение (изоморфизм) между элементами множества и множества , сохраняющее все возможные операции и отношения между ними. Требование изоморфизма зачастую оказывается слишком строгим, поэтому чаще оказывается достаточным условие гомоморфизма алгебраических систем, при котором снимается условие взаимной однозначности отображения , то есть некоторые элементы множества могут иметь один элемент множества в качестве своего образа.

Репрезентативная теория

Репрезентативная теория измерений впервые была представлена в трудах польского, впоследствии американского, математика, представителя Львовско-Варшавской математической школы, Альфреда Тарского и получила наиболее полное оформление в работе П. Зуппеса и Дж. Л. Зиннеса «Basic measurement theory». In R. D. Luce, R. R. Bush, & E. H. Galanter (Eds.), Handbook of Mathematical Psychology, Vol. 1. New York: Wiley, 1963, вышедшей в 1967 году и на русском языке. Постановки тонких математических аспектов репрезентативной теории измерений можно найти в книге профессора И. Пфанцагля «Теория измерений»[7]. – М.: Мир, 1976. – 165 с.

В репрезентативной теории измерений предполагается существование для каждого свойства, подлежащего измерению, некоторой эмпирической системы с отношениями, подобной классам А.А. Фридмана и алгебраическим системам А.И. Мальцева:

,

где - множество проявлений измеряемого свойства объекта или явления,

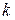- - арные ( 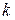- местные) отношения между 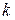элементами множества .

Операции между элементами множества отдельно не рассматриваются[8], а считаются также отношениями. Так двухместная операция сложения трактуется как трехместное отношение между элементами , которое имеет место тогда и только тогда, когда .

К числу отношений относятся, например, следующие отношения:

- двухместное отношение эквивалентности для некоторых элементов , принадлежащих множеству (тела имеют одинаковую массу или температуру, господа обладают одинаковыми умственными способностями); это отношение рефлексивно (), симметрично (если , то ) и транзитивно (если , и то );

- двухместное отношение толерантности ; это отношение подобно эквивалентности, но не является транзитивным ( похоже на , похоже на , но не похоже на );

- двухместное отношение строго порядка ; это отношение не рефлексивно ( неверно), антисимметрично (если , то неверно) и транзитивно (если и то ).

Измерением называется процедура установления гомоморфизма между эмпирической системой с отношениями и соответствующим образом выбранной числовой системой с отношениями , в которой носителем является множество целых чисел, действительных чисел или некоторых других символов с отношениями между ними, которые являются аналогами соответствующих эмпирических отношений . Числовая система является репрезентацией эмпирической системы.

Гомоморфное отображение ставит в соответствие каждому (или нескольким) элементам множества эмпирических объектов единственный объект числового множества , причем таким образом, что если находятся в отношении друг с другом, то их образы находятся друг с другом в отношении .

Это определение более либерально по сравнению с классическим определением измерения и не содержит в себе требования наличия обязательной эмпирической интерпретации алгебраической операции сложения. В тоже время это определение является и более общим. Оно включает в себя все множество классических физических и технических измерений.