 |
Номинальные шкалы (шкалы наименований или классификаций)
|
|
|
|
Наиболее бедной считается эмпирическая система  , между элементами носителя которой могут быть установлены только отношения эквивалентности или неэквивалентности
, между элементами носителя которой могут быть установлены только отношения эквивалентности или неэквивалентности 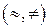 , одинаковости или различия, равенства в каком-то отношении или неравенства
, одинаковости или различия, равенства в каком-то отношении или неравенства  .
.
Каждый элемент носителя 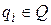 , порождает свой класс эквивалентности
, порождает свой класс эквивалентности  , то есть множество элементов
, то есть множество элементов  носителя, эквивалентных
носителя, эквивалентных  . Множество классов эквивалентности обозначается, как
. Множество классов эквивалентности обозначается, как 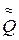 . Эмпирическая система
. Эмпирическая система  преобразуется, таким образом, в неприводимую систему с отношениями
преобразуется, таким образом, в неприводимую систему с отношениями 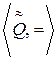 . Если мощность множества
. Если мощность множества 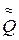 не превышает мощности континуума, то можно построить множество шкал, отображающих
не превышает мощности континуума, то можно построить множество шкал, отображающих 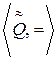 в
в 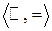 , где
, где  - множество действительных чисел. Это отображение ставит в соответствие каждому классу эквивалентности
- множество действительных чисел. Это отображение ставит в соответствие каждому классу эквивалентности 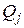 действительное число
действительное число 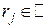 . Эти числа не имеют никакой другой нагрузки, кроме как быть метками соответствующих классов эквивалентности. Вместо чисел можно было бы использовать любые другие символы: словесные описания классов, буквы или комбинации букв любого алфавита и так далее. Класс эквивалентных шкал
. Эти числа не имеют никакой другой нагрузки, кроме как быть метками соответствующих классов эквивалентности. Вместо чисел можно было бы использовать любые другие символы: словесные описания классов, буквы или комбинации букв любого алфавита и так далее. Класс эквивалентных шкал 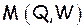 характеризуется тем, что все допустимые гомоморфизмы
характеризуется тем, что все допустимые гомоморфизмы  необходимо являются изоморфизмами между неприводимой эмпирической системой
необходимо являются изоморфизмами между неприводимой эмпирической системой 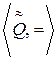 и знаковой системой, которой может быть и числовая система
и знаковой системой, которой может быть и числовая система 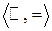 . Группа допустимых преобразований шкалы состоит в этом случае из всех взаимнооднозначных преобразований.
. Группа допустимых преобразований шкалы состоит в этом случае из всех взаимнооднозначных преобразований.
Построенная таким образом шкала и называется номинальной шкалой, шкалой наименований или шкалой классификации. Числовые представления в этой шкале единственны до любого взаимнооднозначного преобразования и являются только метками (сокращенными обозначениями) соответствующих классов эквивалентности на носителе эмпирической системы с отношениями.
|
|
|
Ранговые шкалы (шкалы порядка)
В большинстве встречающихся на практике случаев эмпирическая система с отношениями  содержит в себе, по крайней мере, отношения эквивалентности и строго порядка, благодаря чему носитель системы с отношениями становится упорядоченным множеством
содержит в себе, по крайней мере, отношения эквивалентности и строго порядка, благодаря чему носитель системы с отношениями становится упорядоченным множеством 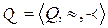 . В частности, упорядоченной является числовая система
. В частности, упорядоченной является числовая система  , носителем которой является множество всех действительных чисел с вполне естественными отношениями равенства и порядка.
, носителем которой является множество всех действительных чисел с вполне естественными отношениями равенства и порядка.
Гомоморфизм 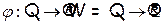 образует ранговую шкалу или шкалу порядка
образует ранговую шкалу или шкалу порядка  . Поскольку в эмпирической системе
. Поскольку в эмпирической системе  и в числовой системе
и в числовой системе 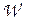 определены только отношения порядка и эквивалентности, то группа допустимых преобразований шкалы
определены только отношения порядка и эквивалентности, то группа допустимых преобразований шкалы 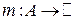 может состоять только из монотонно возрастающих непрерывных отображений. Принято говорить, что ранговая шкала единственна до монотонного преобразования[10].
может состоять только из монотонно возрастающих непрерывных отображений. Принято говорить, что ранговая шкала единственна до монотонного преобразования[10].
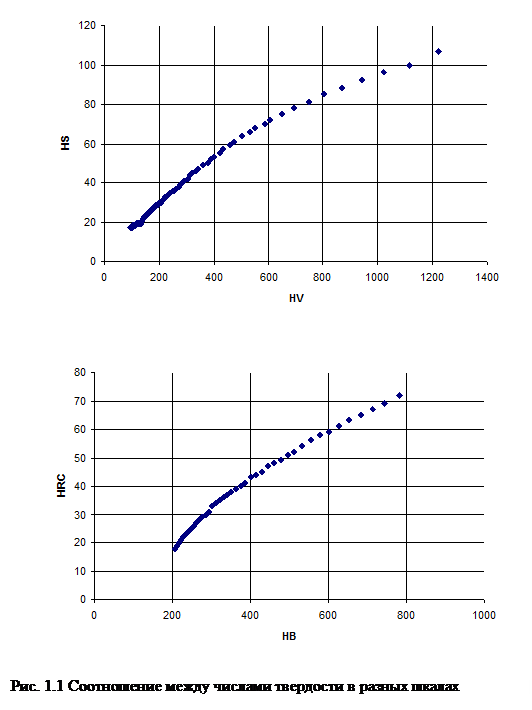
Говорить о какой-то линейности преобразования числовых значений измеряемых величин при переходе от одной шкалы к другой здесь вообще не имеет смысла (см. рис 1.1).
В качестве примеров таких систем можно назвать:
- твердость тел по шкалам Мооса, Бриннеля, Роквелла, Шора,
- умственные способности респондентов по известной шкале IQ,
- успеваемость учащихся по пятибалльной системе или достижения спортсменов в области фигурного катания по десятибалльной шкале,
- скорость выпадения осадка крови как показатель интенсивности патологического процесса.
Для примера на рис.1.1 представлены соотношения между числами твердости в шкалах Виккерса HV и Шора HS, в шкалах Бриннеля HB и Роквелла HRC[11]. Графики ясно показывают, что соотношения между ними нелинейны, но монотонны, а поиск уравнения связи из теоретических соображений к успеху привести не может.
Шкалы интервалов
Во многих случаев упорядоченное множество образуют на только сами элементы носителя эмпирической системы с отношениями, но и их разности, различия в проявлениях измеряемого свойства. Это означает, что на носителе эмпирической системы может быть введена метрика. Сделать это можно только после формирования операционального определения изучаемого свойства, но операциональность определения не является единственным условием для возникновения метрики. Так не зависимо от определения температуры – по расширению ртути или посредством закона Бойля – Мариотта – имеется возможность сравнения температурных интервалов. Сравнение промежутков времени дает одинаковые результаты вне зависимости от того, используется шкала звездного или атомного времени. Но трудно представить себе некую эмпирическую операцию, которая позволила бы сравнить различия в белизне двух пар образцов бумаги или различия в твердости двух пар образцов стали.
|
|
|
Описанная эмпирическая система с отношениями может быть представлена в виде  , где
, где 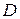 - четырехместное отношение между произвольными элементами
- четырехместное отношение между произвольными элементами  , такое, что
, такое, что 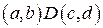 имеет место тогда и только тогда, когда различие между элементами
имеет место тогда и только тогда, когда различие между элементами  и
и  меньше или такое же, как и между элементами
меньше или такое же, как и между элементами  и
и 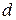 . В соответствующей числовой системе
. В соответствующей числовой системе 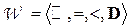 это соответствует введению интервалов между действительными числами.
это соответствует введению интервалов между действительными числами.
Гомоморфизм  образует шкалу интервалов
образует шкалу интервалов 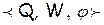 . Поскольку в эмпирической системе
. Поскольку в эмпирической системе  и в числовой системе
и в числовой системе 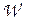 определены отношения порядка и эквивалентности не только между элементами носителей, но и между их интервалами, то группа допустимых преобразований шкалы
определены отношения порядка и эквивалентности не только между элементами носителей, но и между их интервалами, то группа допустимых преобразований шкалы 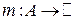 включает в себя все линейные преобразования. Это преобразования типа
включает в себя все линейные преобразования. Это преобразования типа  , где
, где  и
и 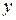 - числовые представления измеряемой величины в двух шкалах, а
- числовые представления измеряемой величины в двух шкалах, а 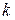 и
и 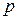 - некоторые постоянные. Принято говорить, что шкала интервалов единственна до линейного преобразования.
- некоторые постоянные. Принято говорить, что шкала интервалов единственна до линейного преобразования.
В шкале интервалов измеряются такие величины как время, электрические потенциалы, температура (шкалы Цельсия, Фаренгейта, Реомюра). Основная особенность этой шкалы заключается в произволе выбора не только единицы измерения (некоторого интервала), но и начала отсчета. Так время можно измерять от Рождества Христова, от сотворения мира или от момента вынужденной эвакуации Пророка и его сподвижников из Мекки в Медину.
Шкалы отношений
|
|
|
На множестве проявлений  некоторых свойств, при их внимательном изучении, иногда удается экспериментально выделить трехмерные отношения
некоторых свойств, при их внимательном изучении, иногда удается экспериментально выделить трехмерные отношения  , подобные сложению, такие, что для любых
, подобные сложению, такие, что для любых 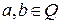 всегда найдется такое
всегда найдется такое 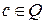 , что имеет место
, что имеет место  . Одновременно на носителе
. Одновременно на носителе  должны быть определены отношения порядка
должны быть определены отношения порядка  и эквивалентности
и эквивалентности  . Операция
. Операция  должна при этом обладать следующими свойствами:
должна при этом обладать следующими свойствами:
- ассоциативность, то есть 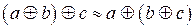 ,
,
- коммутативность 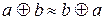 ,
,
- 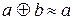 не имеет места, что говорит о бесконечности носителя,
не имеет места, что говорит о бесконечности носителя,
- если  неверно, то найдется такое
неверно, то найдется такое 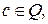 что
что 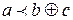 ,
,
- умножению элемента носителя 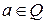 на натуральное число
на натуральное число  равносильно
равносильно  -кратному выполнению операции
-кратному выполнению операции  с этим элементом:
с этим элементом: 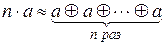 ,
,
- если  , то для каждого
, то для каждого  существует такое
существует такое 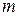 , зависящее от
, зависящее от  , что
, что 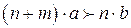 .
.
Эмпирическая система с отношениями 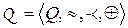 называется экстенсивной системой. Можно показать, что эта система гомоморфна числовой системе с отношениями
называется экстенсивной системой. Можно показать, что эта система гомоморфна числовой системе с отношениями 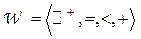 , где
, где 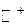 - множество положительных действительных чисел. Наиболее яркое отличие экстенсивной системы от ранее рассмотренных систем заключается в возможности экспериментальной проверки адекватности операции сложения (+) действительных чисел операции сложения
- множество положительных действительных чисел. Наиболее яркое отличие экстенсивной системы от ранее рассмотренных систем заключается в возможности экспериментальной проверки адекватности операции сложения (+) действительных чисел операции сложения 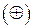 проявлений изучаемого свойства, то есть на множестве элементов носителя эмпирической системы.
проявлений изучаемого свойства, то есть на множестве элементов носителя эмпирической системы.
Гомоморфизм 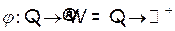 образует шкалу отношений
образует шкалу отношений 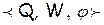 . Поскольку в эмпирической системе
. Поскольку в эмпирической системе  и в числовой системе
и в числовой системе 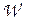 определена (имеет смысл) операция сложения, то группа допустимых преобразований шкалы
определена (имеет смысл) операция сложения, то группа допустимых преобразований шкалы 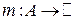 включает в себя только преобразование подобия. Это преобразования типа
включает в себя только преобразование подобия. Это преобразования типа  , где
, где  и
и 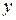 - числовые представления измеряемой величины в двух шкалах, а
- числовые представления измеряемой величины в двух шкалах, а 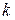 - некоторая постоянная. Принято говорить, что шкала интервалов единственна до преобразования подобия. В отличие от шкалы интервалов в шкале отношений однозначно определен нуль
- некоторая постоянная. Принято говорить, что шкала интервалов единственна до преобразования подобия. В отличие от шкалы интервалов в шкале отношений однозначно определен нуль  .
.
В шкале отношений измеряются все физические величины - величины, входящие в уравнения физики. Поэтому в литературе по теории измерений можно встретить высказывания о том, что «в физике теория измерений не нужна».
|
|
|


