Измерительные информационные технологии

По мере своего развития измерительные информационные системы все в большей степени приобретают черты информационных аналитических систем специализированного направления, широко использующие для решения поставленных перед ними задач методы анализа данных (Data Analysis), машинного обучения (Machine Learning) и искусственного интеллекта (Artificial Intelligence) (рис. 1).

Признаки, характеризующие объект или процесс наблюдения (из генеральной совокупности объектов или процессов) или состояние объекта или процесса (из множества возможных состояний) воспринимаются полем сенсоров, образующих систему до̀бычи данных (Data Mining). Полученные данные подвергаются статистическому анализу (Data Analysis), результатом чего становятся знания об объекте (состоянии объекта) или процессе (состоянии процесса) наблюдения.

Блок управления полем сенсоров активизируется по команде системы анализа данных и осуществляет сканирование объекта сенсорами в пространстве (перемещением сенсоров или изменением направления их чувствительности) и во времени (изменением частоты опроса сенсоров и скорости дискретизации). Полученные знания проверяются на достоверность (Analysis of Validity) и при недостаточной достоверности по-своему активизируют блок управления сенсорной системы.

В качестве объектов исследования может выступать:

- технологический или природный объект при осуществлении наблюдения и контроля над ними,

- производственная система или ее отдельные элементы при идентификации их математических моделей,

- организм человека или животного при диагностировании заболеваний,

- изделия или партии изделий при их контроле или сортировке,

- сигналы и сообщения при их идентификации,

- подлежащие распознаванию летательные объекты или скопления живой силы и техники,

- средства измерений при их первичной или периодической поверке.

Полученные знания представляются в форме некоторых классификаций. Технологический или природный объект может оказаться принадлежащим одному из классов состояний (работоспособный, предаварийный, аварийный, катастрофически размножились некоторые вредители лесных угодий, пересохли водоёмы и так далее).

Производственная система или технологический процесс может находиться в удовлетворительном состоянии и выдавать годную продукцию, уровень настройки может приблизиться к критическому значению, технологическое рассеивание может находиться в предписанных нормах или достигать неприемлемых значений.

Человек может быть здоровым или его организм претерпевает те или иные изменения и наступает опасность возникновения различных нарушений.

Производимые или покупаемые изделия могут быть годными или дефектными по одному или нескольким признакам качества.

Партии изделий могут иметь удовлетворительное качество или быть дефектными по некоторым признакам качества.

Сигналы могут быть просто шумами или сигналами, несущими осмысленные сообщения, сообщения, предназначенные для всех или только для того или иного потребителя.

В любом случае мы имеем объект исследования, который характеризуется набором признаков - транспонированным вектором признаков в - мерном пространстве признаков. Структура этого пространства определяется отношениями между значениями признаков, то есть теми шкалами, по которым производится измерение признаков.

Результатом когнитивной деятельности системы становится отнесении исследуемого объекта к тому или иному классу объектов , множество которых образует вектор . Поэтому классам объектов или состояний объектов можно поставить в соответствие некоторые подмножества в пространстве признаков. Эти подмножества определяют разбиение пространства признаков, так что . Если вектор , соответствующий данному объекту , попадает в подмножество , то это означает, что объект принадлежит классу .

Классы объектов могут задаваться нормами на значения признаков объектов или формироваться по заранее задаваемым критериям в процессе обучения или самообучения системы (Machine Learning).

Погрешности измерения признаков объектов, недостатки алгоритмов анализа данных и нечеткости определения границ между классами объектов приводят к возникновению ошибок реализации классификаций, заключающихся в том, что объекты, действительно относящиеся к одному классу, после проведения классификации оказываются в другом классе объектов. Это ограничивает достоверность (Validity) классификаций, задаваемых информационной системой.

В результате проведения измерений сенсорная система преобразует вектор признаков в вектор результатов измерений – случайных величин, отягощенных погрешностями измерений:

.

Погрешности измерений образуют случайный вектор:

.

Распределение этого вектора можно охарактеризовать совместной плотностью распределения:

,

где - возможные реализации значений погрешностей .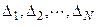

Следует, однако, помнить, что и сами признаки на множестве наблюдаемых объектов или состояний объектов являются случайными величинами со своей совместной плотностью распределения:

и условными плотностями признаков объектов, классифицированных по классам объектов:

.

Совместная плотность распределения результатов измерения признаков определяется как результат многомерной свертки плотностей распределения самих признаков и погрешностей их измерения:

так что

Достоверность процедуры (контроля, диагностики, идентификации моделей, распознавания образов) характеризуется вектором оперативных характеристик, соответствующих классам объектов:

Каждый элемент этого вектора - оперативная характеристика - определяется как вероятность отнесения объекта со значениями признаков к классу , что является следствием попадания наблюдаемой точки , но вовсе не точки , в область . Области с точки зрения теории проверки статистических гипотез являются допустимыми для принятия решения об отнесении объекта или состояния объекта к классу , поэтому:

Пример

Контролю подлежат изделия типа роликов по диаметру (признак ) и по отклонению от круглости (признак ). Пространство признаков - это верхняя полуплоскость с осями . Нормы на значения контролируемых величин и разбивают все пространство признаков на шесть подмножеств и определяют 6 классов контролируемых изделий.

 

Классы изделий	Области в пространстве признаков	Границы областей	Наименования классов
			Класс годных изделий
			Классы (виды) брака

 

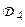
Будем считать погрешности измерения признака диаметра изделия и независимыми случайными величинами. Погрешность измерения признака распределена нормально:

со стандартным отклонением .

 

 

Для погрешности измерения признака примем отраженное нормальное распределение, формируемое в программе Math Cad следующим образом:

Здесь стандартное отклонение погрешности , а параметр примем равным нулю. Тогда совместная плотность распределения погрешностей измерения признаков может быть представлена в виде:

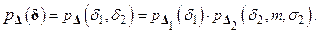
Результаты измерений признаков изделия с учетом погрешностей их измерения становятся теперь случайными величинами с плотностями распределения:

,

где имеют смысл действительных значений признаков изделия.

Теперь имеются все необходимые данные для вычисления всех шести оперативных характеристик для всех шести установленных классов. Для класса оперативная характеристика принимает вид:

Если задаться следующими данными:

то получим оперативную характеристику для класса , представленную на рис. 2 в форме двухмерной поверхности и в виде совокупности линий одного уровня (контурной карты).

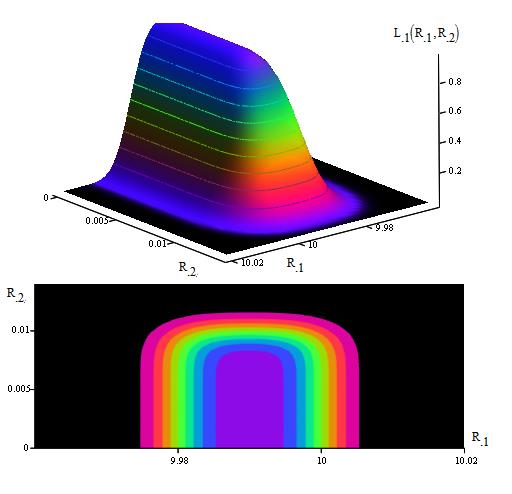
Рис. 2

Рис. 2 наглядно показывает, что далеко не все объекты, действительно принадлежащие к классу , принимаются в этот класс по результатам проводимой классификации. Более тог, объекты из соседних классов с некоторыми конечными вероятностями принимаются в этот класс.

На рис. 3 показаны те же характеристики, но для класса . Здесь наблюдается та же ситуация, что и для класса . Не все объекты, принадлежащие данному классу, принимаются в этот класс. Но с некоторыми конечными вероятностями в этот класс принимаются объекты, на самом деле принадлежащие другим классам.

Рис. 3

 

Таким образом, аппаратная реализация классификации сопровождается появлением ошибок классификации, связанных с погрешностями измерения признаков объектов..

С одной стороны, в каждый класс попадают не все объекты, действительно принадлежащие данному классу. С вероятностями

,

которые зависят от действительных значений признаков , объекты с этими значениями признаков, будут отторгнуты из этого класса и перемещены в другие классы. В теории проверки статистических гипотез эти ошибки называются ошибками первого рода. После определения оперативных характеристик вероятности ошибок первого рода можно вычислить для каждого класса объектов.

Так на рис. 4 показано распределение вероятности ошибки первого рода для области , соответствующей классу годных изделий.

Рис. 4

 

Но в соответствии с оперативной характеристикой каждого данного класса в число элементов класса будут приняты объекты других классов, будут приняты с вероятностями, зависящими от действительных значений их признаков. Это ошибки второго рода. Эти вероятности различны для различных классов, из которых объекты просачиваются в рассматриваемый класс. Их число равно , то есть на единицу меньше числа классов объектов. Вероятности ошибок второго рода вычисляются следующим образом:

.

Здесь - это вероятность того, что объект, принадлежащий классу , будет по результатам измерений отнесен к классу .

На рис. 5 представлены графики зависимостей вероятностей ошибок второго рода:

,

, , ,

.

Рис. 5

Графики построены по данным рассмотренного выше примера в обычном 3d-представлении и в контурном изображении Аналогичные картины могут быть построены и для всех других классов объектов.

Таким образом, вероятности ошибок при реализации классификации можно представить в виде единой матрицы вероятностей ошибок:

На главной диагонали здесь находятся вероятности ошибок первого рода для классов объектов, на остальных местах находятся вероятности ошибок второго рода – вероятности отнесения к классу, стоящему на первом месте после вертикальной черты, объекта, на самом деле принадлежащего к классу, стоящему на втором месте, после диагональной черты.

Полученные зависимости позволяют проследить процесс формирования ошибок первого и второго рода в зависимости от конкретных значений признаков вблизи границ разбиения признакового пространства. Иллюстрации, представленные на рисунках, дают наглядную картину распределения ошибок только в случае использования двух признаков. При произвольном числе признаков приходится отказываться от наглядности геометрического представления.

Для практических целей, связанных, например, с выбором элементов сенсорной системы, анализом брака или оценкой эффективности системы, реализующей те или иные измерительные информационные технологии, важно знать усредненные характеристики достоверности результатов машинной классификации.

Предположим, что признаки объекта исследований являются случайными величинами с совместной плотностью распределения

,

где - возможные значения признаков .

Если признаки являются независимыми случайными величинами, то совместная плотность их распределения распадается на произведение одномерных плотностей распределения признаков:

.

Знание плотности распределения признаков делает возможным определение следующих характеристик достоверности проводимой классификации.

1. Плотности распределения значений признаков объектов, отнесенных к тем или иным классам объектов:

.

В рассматриваемом нами примере примем для диаметра изделия (признак ) нормальное распределение с математическим ожиданием и стандартным отклонением . Плотность распределения признака принимает вид:

.

Для отклонения от круглости (признак ), как для положительной величины, примем отраженное нормальное распределение:

с параметрами и

Плотность совместного распределения признаков

графически представлена на рис. 6 и 7. Распределение захватывает практически все выделенные области в пространстве признаков.

Теперь посмотрим, как будет выглядеть распределение признаков для объектов, попавших по результатам классификации в класс :

при ранее определенной оперативной характеристики .

 

Рис. 6

Рис. 7

 

Результаты расчетов, проведенные в программе Math Cad, дают результаты, представленные на рис. 8. Сравнение графиков на рис. 6, 7 и 8 наглядно показывают процесс выделения класса из предложенной системе совокупности объектов.

Для сравнения построим распределение признаков объектов из той же совокупности, но отнесенных системой к классу .

Результаты расчетов приведены на второй паре рис. 8 и 9.

 

Рис. 8 и 9

2. Средние по классам вероятности ошибок первого рода:

. .

3. Средние по классам вероятности ошибок второго рода – вероятности проникновения в данный класс объектов из других классов :

.

4. Суммарная доля чужеродных объектов в классах объектов после проведения классификации – суммарная вероятность ошибки второго рода:

.

5. Каждый класса объектов порождает матрицу условных математических ожиданий совокупностей объектов, принятых в этот класс и ошибочно отнесенных к другим классам объектов:

.

Матрица имеет размеры в соответствии с числом строк, равным числу классов объектов, и числу столбцов, равным числу признаков. Элементы строки определяют положение центра группирования той совокупности объектов класса , которые по результатам измерений попали в класс, соответствующий номеру строки. Каждый элемент матрицы вычисляется путём интегрирования по соответствующей области пространства признаков с использованием плотности совместного распределения признаков предъявленных системе объектов, отнесённых системой к классам :

Всего можно построить таких матриц, соответствующих классам объектов.

6. Расстояния между совокупностями объектов, порожденных ошибками их классификации в класс , можно вычислить или как евклидову норму разности соответствующих строк соответствующих матриц условных математических ожиданий:

,

либо как вектор расстояний между центрами группирования по осям координат пространства признаков:

7. Матрица дисперсий.

8. доверительные расстояния и вектор доверительных расстояний.

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: