Математическая модель участка выхода на режим, процессов при прорыве магистрали нагнетания и разгерметизации диафрагмы бака после опорожнения жидкости.
Практика отработки газогидравлических преобразователей совместно с ТГ показала, что наиболее сложным для описания физических процессов и проектирования является нестационарный участок, связанный с запуском и выходом на режим заданной мощности.
В данном разделе представлено описания участка выхода на режим заданной мощности ТГ с ВИП обыкновенными дифференциальными уравнения газовой и гидродинамики, а также рассмотрены возможные случаи аномальной работы элементов газовой и гидравлической систем. Для иллюстрации достоверности полученных результатов математического моделирования привлечены данные экспериментальных результатов натурных образцов.
При построении математической модели участка выхода на режим по давлениям газа и нагнетания рабочей жидкости и случаев аномальной работы использованы следующие основополагающие уравнения физики:
1. Уравнение баланса массового секундного прихода и расхода газа в ТГ с учётом работы газового клапана – уравнение Бори,
2. Уравнение состояния газа в камере сгорания ТГ и газовой полости ВИП,
3. Уравнение баланса расхода рабочей жидкости в баке ПАД`а и потребителе,
4. Уравнение баланса сил, действующих со стороны газовой полости на металлическую подвижную диафрагму вытеснителя и сил сопротивления движению диафрагмы со стороны жидкостной полости бака ПАД`а.
Известно, что секундный газоприход от ТГ уравновешивается расходом газа, затрачиваемым на заполнение увеличивающегося вследствие вытеснения жидкости из бака газового объёма полости вытеснителя, расходом газа через газовый клапан и расходом газа, затрачиваемым на заполнение объёма, образованного в результате сжатия газа в камере сгорания ТТ, в газовом объёме вытеснителя и воздушного объёма жидкостной полости.
С учётом степенного закона зависимости скорости горения от давления, уравнения состояния газа в газовой полости вытеснителя, линейной зависимости непроизводительного расхода жидкости от давления и сверхкритического истечения газа через клапан, неподвижного состояния РМ, уравнение баланса записывается в виде для Р > P0:
 , (7.1)
, (7.1)
где 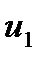 - коэффициент чувствительности скорости горения к температуре заряда твёрдого топлива,
- коэффициент чувствительности скорости горения к температуре заряда твёрдого топлива, 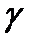 - удельный вес топлива,
- удельный вес топлива, 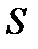 - поверхность горения топлива,
- поверхность горения топлива, 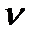 - показатель степени в законе горения топлива,
- показатель степени в законе горения топлива, 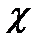 - коэффициент тепловых потерь газа в объёме бака вытеснителя,
- коэффициент тепловых потерь газа в объёме бака вытеснителя, 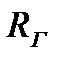 - удельная газовая постоянная продуктов сгорания топлива,
- удельная газовая постоянная продуктов сгорания топлива, 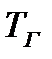 - температура газа,
- температура газа,  - коэффициент истечения газа,
- коэффициент истечения газа, 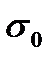 - площадь проходного сечения, образованного зазором между клапаном и седлом в закрытом состоянии,
- площадь проходного сечения, образованного зазором между клапаном и седлом в закрытом состоянии, 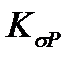 - коэффициент пропорциональности между проходным сечением клапана и давлением в зоне регулирования.
- коэффициент пропорциональности между проходным сечением клапана и давлением в зоне регулирования.
Для Р < P0 уравнение баланса прихода и расхода при течении газа через минимальное сечение клапана, образованного его положением на седле, преобразуется к виду:
 , (7.2).
, (7.2).
Уравнения (7.1) и (7.2) описывают процессы, протекающие в газовой части ПАД`а, до диафрагмы.
После использования преобразования Лапласа запишем уравнения работы ПАД в операторной форме:
, (7.3)
где 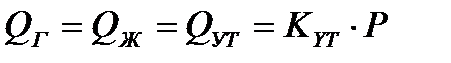 .
.
Уравнения, описывающие процессы за диафрагмой в полости бака с рабочей жидкостью и воздушной средой, составлены на основании использования уравнений неразрывности (сплошности) потока жидкости, сжатия рабочей жидкости в нагнетательной полости гидросистемы, состояния коагулированных пузырьков растворённого воздуха в виде газового объёме в жидкости, находящейся в баке.
Объёмный расход газа  в газовой части ПАД, используется для компенсации расходов на сжатие воздушной среды и вытеснения жидкости из полости бака, в виде:
в газовой части ПАД, используется для компенсации расходов на сжатие воздушной среды и вытеснения жидкости из полости бака, в виде:
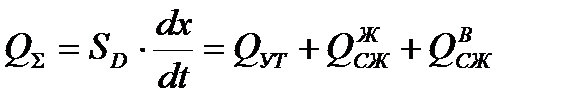 , (7.4)
, (7.4)
где: 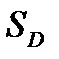 - площадь диафрагмы, х – перемещение диафрагмы,
- площадь диафрагмы, х – перемещение диафрагмы,  - расход жидкости в плоских зазорах золотников РМ,
- расход жидкости в плоских зазорах золотников РМ, 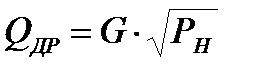 - расход через дроссель (G – проводимость дросселя), подключаемый к магистрали нагнетания (в случае имитация разгерметизации),
- расход через дроссель (G – проводимость дросселя), подключаемый к магистрали нагнетания (в случае имитация разгерметизации), 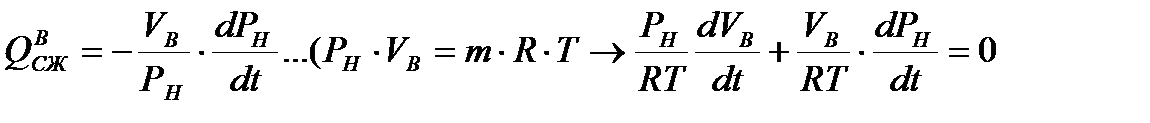 ) – расход на сжатие воздуха в баке (VB – объём воздушной среды бака до его сжатия, m – масса воздуха в жидкостной полости бака),
) – расход на сжатие воздуха в баке (VB – объём воздушной среды бака до его сжатия, m – масса воздуха в жидкостной полости бака), 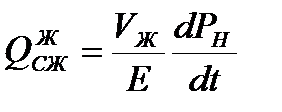 (VЖ – объём жидкости в полости бака, Е – объёмный модуль упругости рабочей жидкости).
(VЖ – объём жидкости в полости бака, Е – объёмный модуль упругости рабочей жидкости).
После подстановки составляющих расхода уравнение баланса расхода примет вид:
, (7.5).
Используя оператор преобразования Лапласа, уравнение (7.5) примет вид:
(7.6)
Уравнение нагрузки, действующей на диафрагму, в соответствии с уравнением баланса сил и учётом инерционности массы жидкости
, имеет вид:
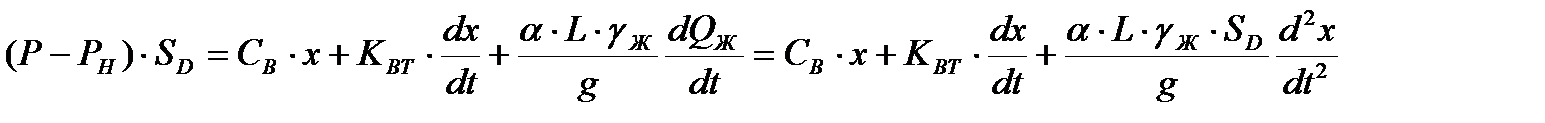 , (7.7)
, (7.7)
где 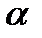 =1,1 –коэффициент количества движения, не зависящий от времени, L – максимальный ход диафрагмы до полного вытеснения жидкости из бака, g = 980
=1,1 –коэффициент количества движения, не зависящий от времени, L – максимальный ход диафрагмы до полного вытеснения жидкости из бака, g = 980  - ускорение свободного падения,
- ускорение свободного падения, 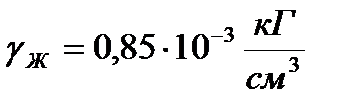 - уд. вес рабочей жидкости,
- уд. вес рабочей жидкости, 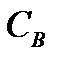 - суммарная жёсткость диафрагмы и воздушной пружины (величина, определяемая в ходе моделирования),
- суммарная жёсткость диафрагмы и воздушной пружины (величина, определяемая в ходе моделирования),  - коэффициент вязкого трения (определяется течением жидкости в плоском зазоре золотников РМ).
- коэффициент вязкого трения (определяется течением жидкости в плоском зазоре золотников РМ).
Применив преобразование Лапласа к уравнению (7.7), получим выражение для перемещения диафрагмы в виде:
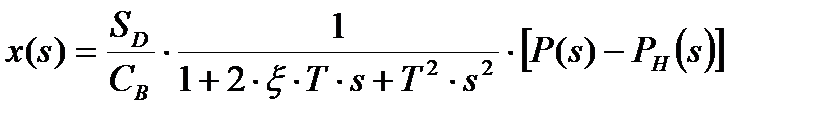 , (7.8)
, (7.8)
где
- постоянная времени жидкостной полости ПАД`а с учётом наличия в ней воздушной полости,
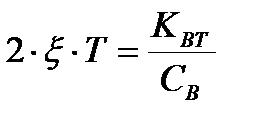
- комплекс, учитывающий действие вязкого трения рабочей жидкости при течении в плоском зазоре золотника.
Приравняв (7.6) и (7.8), получим уравнение гидравлической части ПАД`а в виде соотношения:
, (7.9)
После преобразования в формат, удобный для построения структурной схемы математической модели, уравнение (8) будет иметь вид:
(7.10)
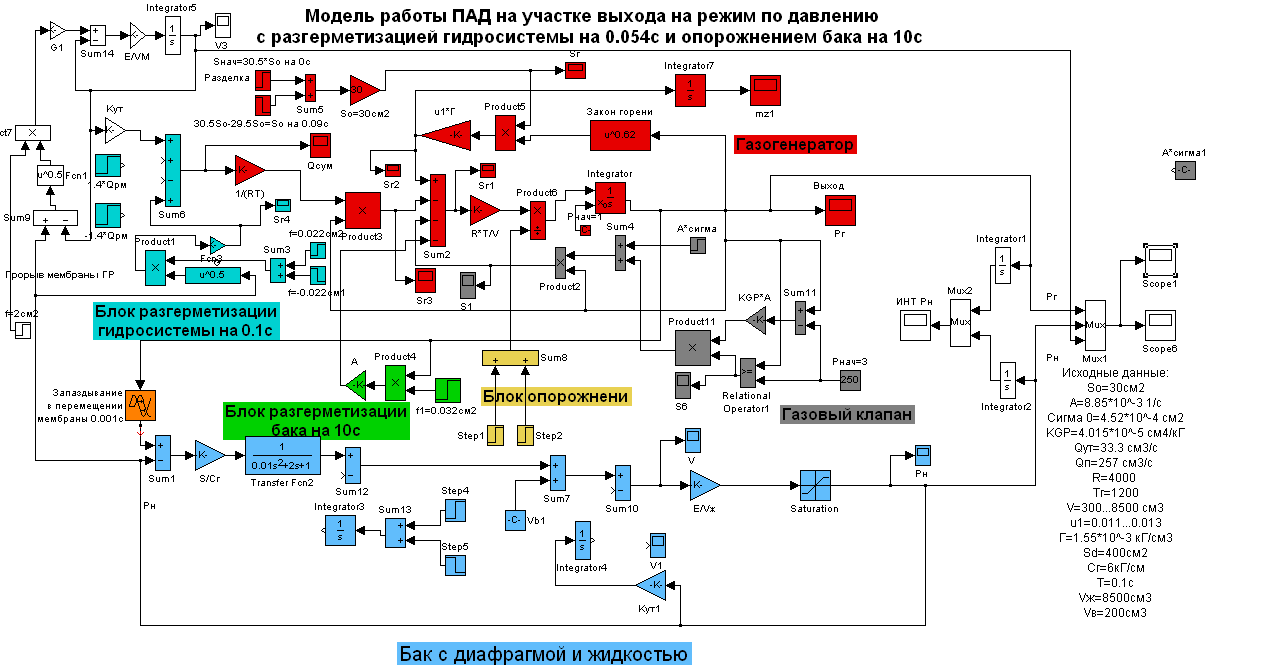
Структурная схема обобщённой модели газового и гидравлического контуров, построеннойая на основании уравнений (7.3) и (7.10), представлена на рис. 7.1.
Переходный процесс изменения давлений Р(t) и РН(t) представлен на рис. 7.2 для следующих параметров модели при разгерметизации гидростистемы в магистрали нагнетания на 0.054с:
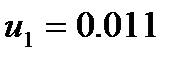 ;
;  ;
; 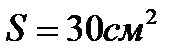 ;
; 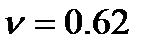 ;
; 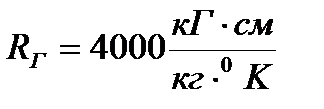 ;
; 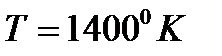 ;
;  ;
; 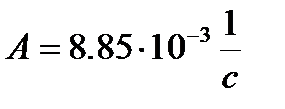 ;
;  ;
; 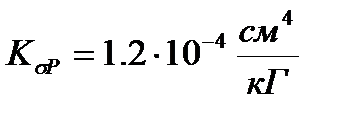 ;
; 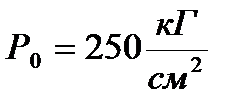 ;
; 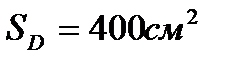 ;
;  ;
; 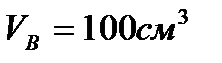 ;
;  ;
; 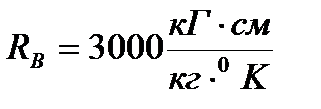 ;
; 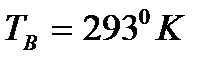 ;
;  ;
; 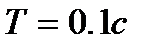 ;
; 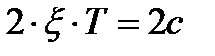 ;
;  .
.
Разгерметизация гидросистемы представлена в модели отдельным контуром бирюзового цвета, составленным из нелинейного звена извлечения корня из  , звена умножения
, звена умножения  (где f = 0.022cм2 – условное сечение отверстия разгерметизации) и проводимости отверстия
(где f = 0.022cм2 – условное сечение отверстия разгерметизации) и проводимости отверстия  (где
(где 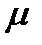 - коэффициент истечения потока жидкости
- коэффициент истечения потока жидкости
- плотность жидкости).
На рис. 7.3 к переходному процессу на рис. 7.2 добавлен переходной процесс изменения давления при разгерметизации диафрагмы после опорожнения бака на 10с. Разгерметизация диафрагмы представлена в модели отдельным контуром зелёного цвета и реализована подключением на 10с к блоку суммарного расхода газа звена, характеризующего сверхкритическое истечение газа из полости бака через условное сечение отверстия разгерметизации гидросистемы в окружающую среду. Одновременно на 10с в звене сжимаемости газа в газовой полости объём газовой полости заменялся при реализации нелинейного блока деления (жёлтого цвета) с величины 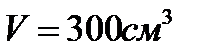 на
на 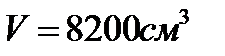 .
.
На рис. 7.4, 7.4а представлены процессы изменения давления, полученные в ходе эксперимента, которые по качественным и количественным показателям близки к результатам моделирования рис. 7.2.
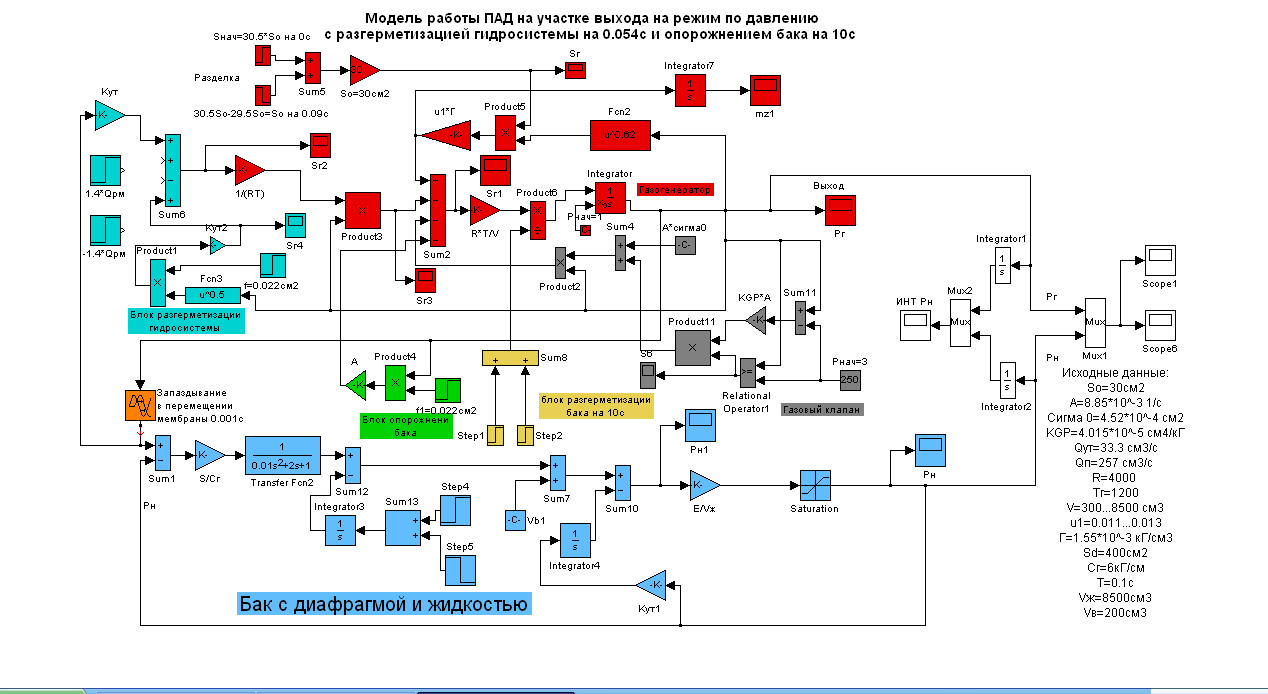
Рис. 7.1. Структурная схема обобщённой модели газовой и гидравлической частей
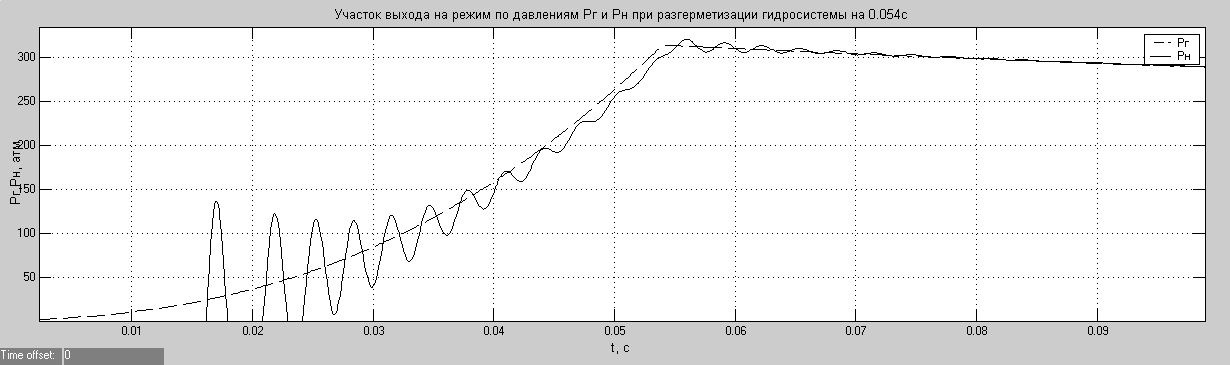
Рис. 7.2. Переходный процесс изменения давлений Р(t) и РН(t)
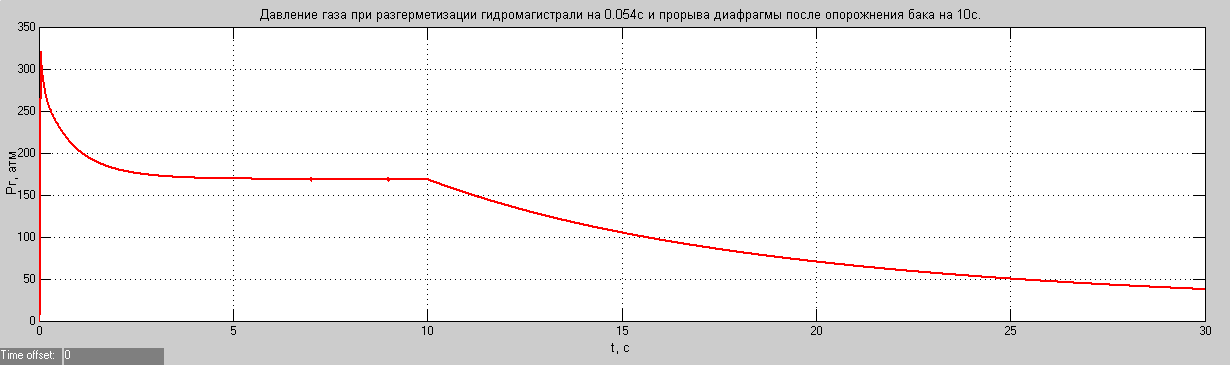
Рис. 7.3. Переходный процесс изменения давления при разгерметизации бака после опорожнения жидкости
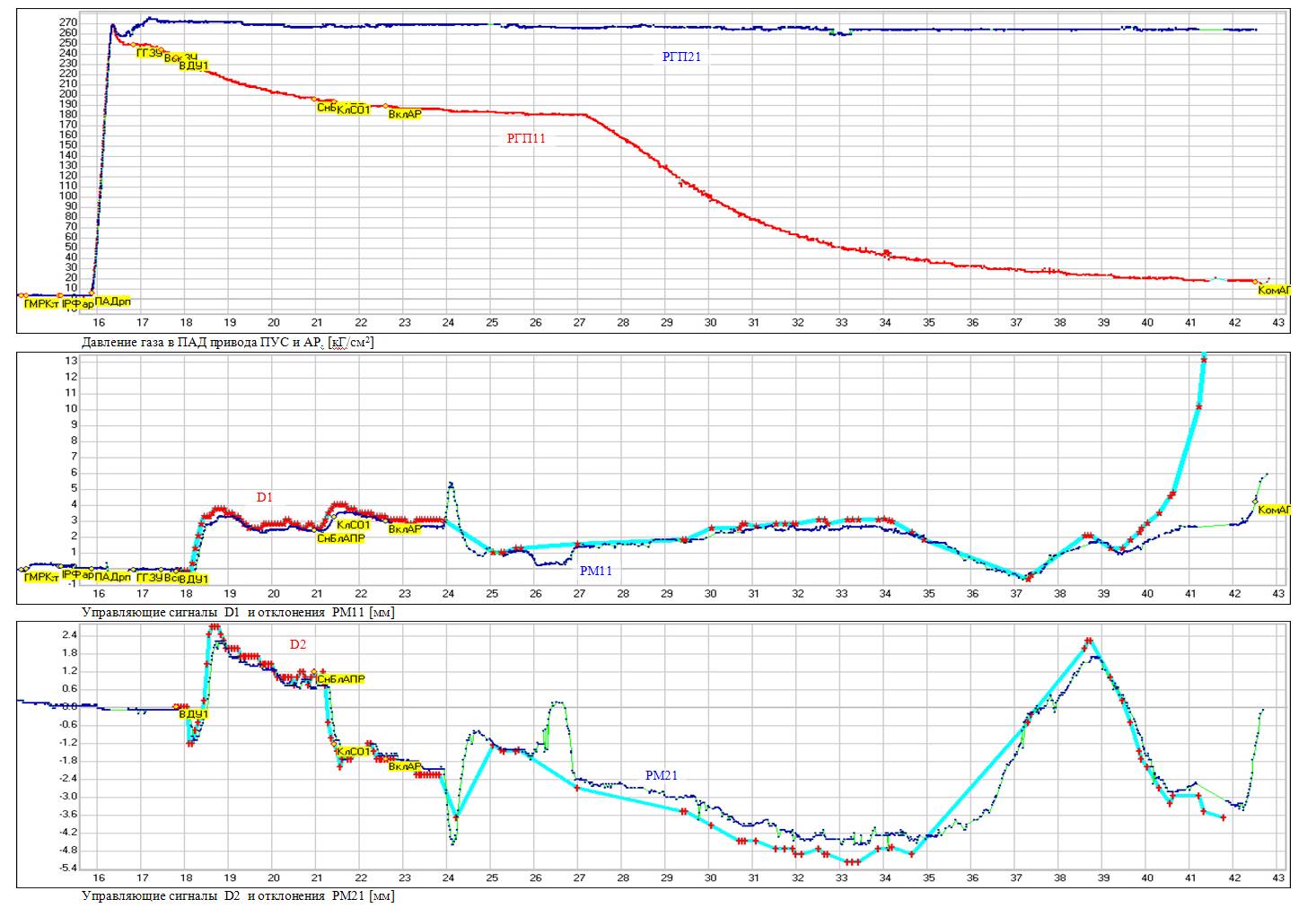
Рис. 7.4. Переходный процесс изменения давления при разгерметизации бака после опорожнения жидкости
(экспериментальные данные)
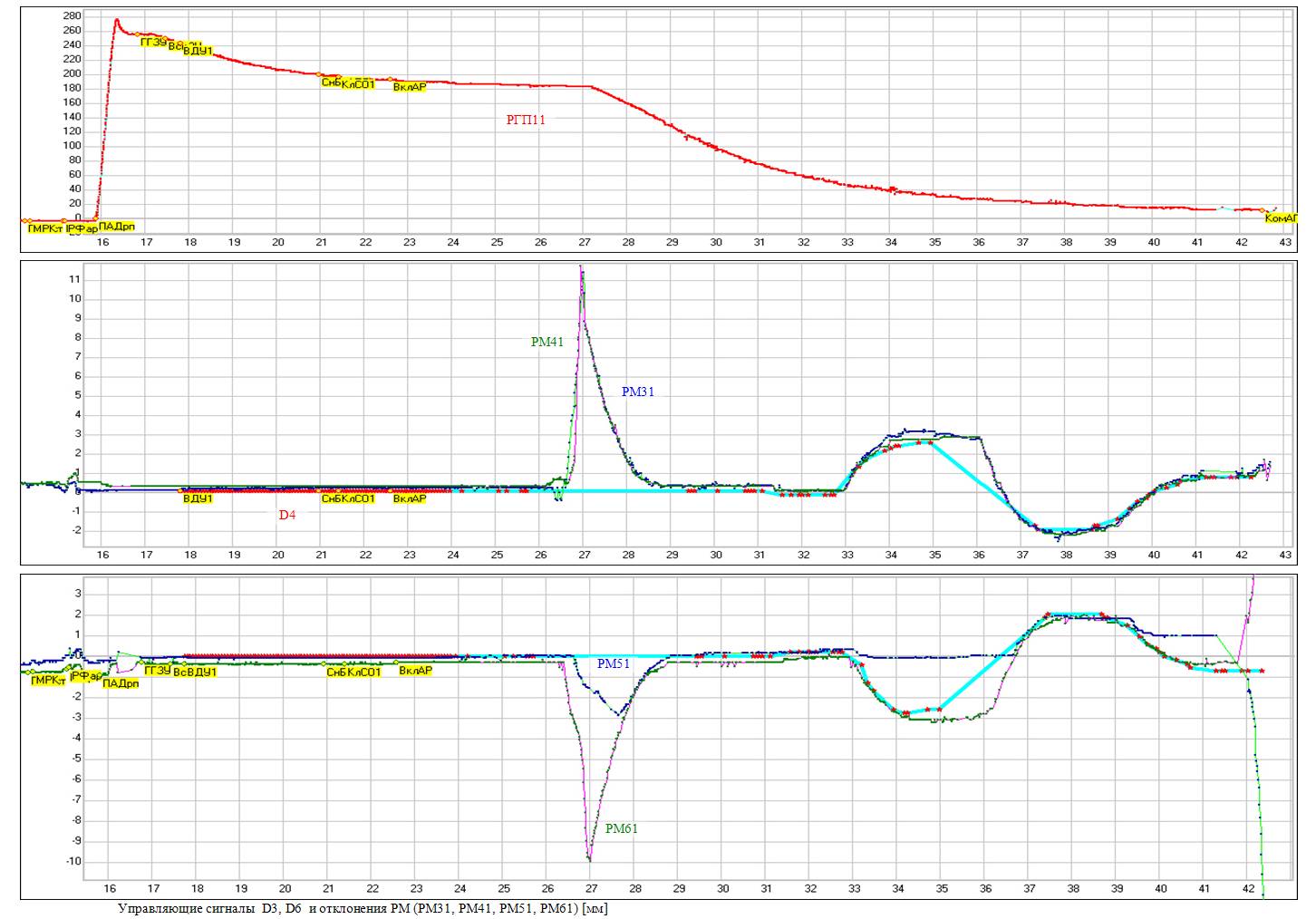
Рис. 7.4.а. Переходный процесс изменения давления при разгерметизации бака после опорожнения жидкости
(экспериментальные данные)
Варьируя величиной воздушного объёма VB в диапазоне 0…400см3, образующегося в баке рабочей жидкости, на рис. 7.5 представлен график зависимости максимальной амплитуды первого импульса затухающего колебательного процесса изменения давления жидкости в баке ПАД`а от VB (Pmax=f(VB)), полученный в результате моделирования участка выхода на режим рис. 7.2.
Рmax, кГ/см2
 V, см3
V, см3
Рис. 7.5. Зависимость Pmax=f(VB)
Ниже на рис. 7.6 представлена модель, построенная с учётом реализации прорыва мембраны, установленной перед гидроразъёмом бака (блок прорыва мембраны – звенья белого цвета). Участок выхода на режим по давлениям в газовой полости бака Рг, в жидкостной полости бака Рб и в магистрали нагнетания Рж иллюстрирует рис. 7.7.
Воспользуйтесь поиском по сайту:


 , (7.1)
, (7.1)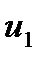 - коэффициент чувствительности скорости горения к температуре заряда твёрдого топлива,
- коэффициент чувствительности скорости горения к температуре заряда твёрдого топлива, 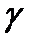 - удельный вес топлива,
- удельный вес топлива, 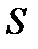 - поверхность горения топлива,
- поверхность горения топлива, 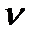 - показатель степени в законе горения топлива,
- показатель степени в законе горения топлива, 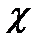 - коэффициент тепловых потерь газа в объёме бака вытеснителя,
- коэффициент тепловых потерь газа в объёме бака вытеснителя, 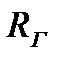 - удельная газовая постоянная продуктов сгорания топлива,
- удельная газовая постоянная продуктов сгорания топлива, 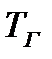 - температура газа,
- температура газа,  - коэффициент истечения газа,
- коэффициент истечения газа, 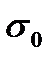 - площадь проходного сечения, образованного зазором между клапаном и седлом в закрытом состоянии,
- площадь проходного сечения, образованного зазором между клапаном и седлом в закрытом состоянии, 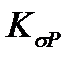 - коэффициент пропорциональности между проходным сечением клапана и давлением в зоне регулирования.
- коэффициент пропорциональности между проходным сечением клапана и давлением в зоне регулирования. , (7.2).
, (7.2).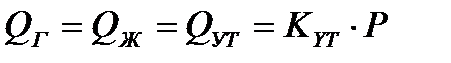 .
. в газовой части ПАД, используется для компенсации расходов на сжатие воздушной среды и вытеснения жидкости из полости бака, в виде:
в газовой части ПАД, используется для компенсации расходов на сжатие воздушной среды и вытеснения жидкости из полости бака, в виде: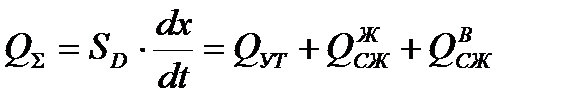 , (7.4)
, (7.4)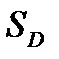 - площадь диафрагмы, х – перемещение диафрагмы,
- площадь диафрагмы, х – перемещение диафрагмы,  - расход жидкости в плоских зазорах золотников РМ,
- расход жидкости в плоских зазорах золотников РМ, 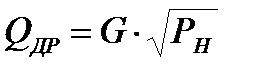 - расход через дроссель (G – проводимость дросселя), подключаемый к магистрали нагнетания (в случае имитация разгерметизации),
- расход через дроссель (G – проводимость дросселя), подключаемый к магистрали нагнетания (в случае имитация разгерметизации), 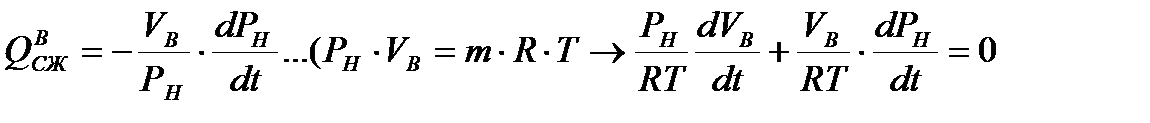 ) – расход на сжатие воздуха в баке (VB – объём воздушной среды бака до его сжатия, m – масса воздуха в жидкостной полости бака),
) – расход на сжатие воздуха в баке (VB – объём воздушной среды бака до его сжатия, m – масса воздуха в жидкостной полости бака), 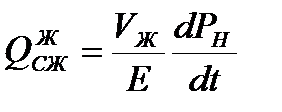 (VЖ – объём жидкости в полости бака, Е – объёмный модуль упругости рабочей жидкости).
(VЖ – объём жидкости в полости бака, Е – объёмный модуль упругости рабочей жидкости).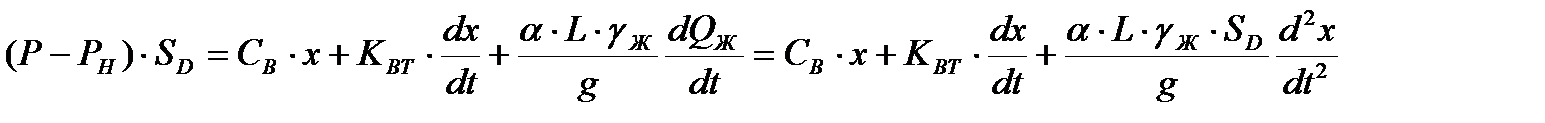 , (7.7)
, (7.7)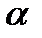 =1,1 –коэффициент количества движения, не зависящий от времени, L – максимальный ход диафрагмы до полного вытеснения жидкости из бака, g = 980
=1,1 –коэффициент количества движения, не зависящий от времени, L – максимальный ход диафрагмы до полного вытеснения жидкости из бака, g = 980  - ускорение свободного падения,
- ускорение свободного падения, 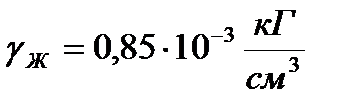 - уд. вес рабочей жидкости,
- уд. вес рабочей жидкости, 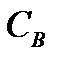 - суммарная жёсткость диафрагмы и воздушной пружины (величина, определяемая в ходе моделирования),
- суммарная жёсткость диафрагмы и воздушной пружины (величина, определяемая в ходе моделирования),  - коэффициент вязкого трения (определяется течением жидкости в плоском зазоре золотников РМ).
- коэффициент вязкого трения (определяется течением жидкости в плоском зазоре золотников РМ).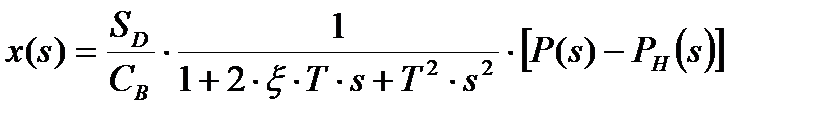 , (7.8)
, (7.8)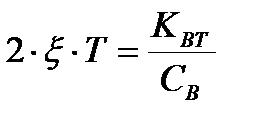 - комплекс, учитывающий действие вязкого трения рабочей жидкости при течении в плоском зазоре золотника.
- комплекс, учитывающий действие вязкого трения рабочей жидкости при течении в плоском зазоре золотника.
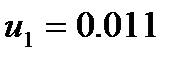 ;
;  ;
; 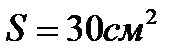 ;
; 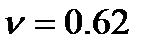 ;
; 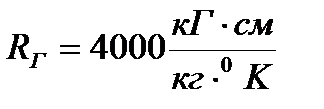 ;
; 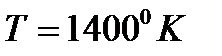 ;
;  ;
; 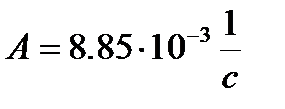 ;
;  ;
; 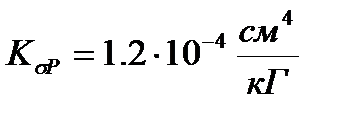 ;
; 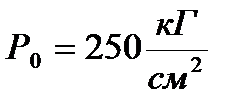 ;
; 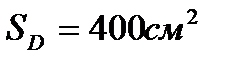 ;
;  ;
; 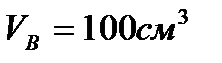 ;
;  ;
; 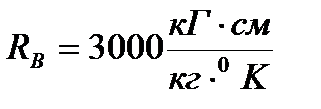 ;
; 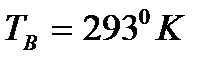 ;
;  ;
; 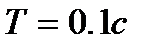 ;
; 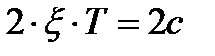 ;
;  .
. , звена умножения
, звена умножения  (где f = 0.022cм2 – условное сечение отверстия разгерметизации) и проводимости отверстия
(где f = 0.022cм2 – условное сечение отверстия разгерметизации) и проводимости отверстия  (где
(где 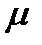 - коэффициент истечения потока жидкости
- коэффициент истечения потока жидкости 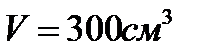 на
на 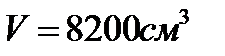 .
.




 V, см3
V, см3


