Оценка качества модели множественной регрессии: F-критерий Фишера, t-критерий Стьюдента. Мультиколлинеарность. Методы устранения мультиколлинеарности.

Значимость уравнения множественной регрессий в целом, так же как и в парной регрессии, оценивается с помощью F-критерия Фишера:

                                       (3.32)

Где  - факторная сумма квадратов на одну степень свободы;

    - остаточная сумма квадратов на одну степень свободы;

      - коэффициент (индекс) множественной детерминации;

  m - число параметров при переменных х (в линейной регрессии совпадает с числом включенных в модель факторов);

n   - число наблюдений.

Оценивается значимость не толь ко уравнения в целом, но и фактора, дополнительно включенного в регрессионную модель. Необходимость такой оценки связана с тем, что не каждый фактор, вошедший вариации в модель, может существенно увеличивать долю объясненной вариации результативного признака. Кроме того, при наличии в модели нескольких факторов они могут вводиться в модель в разной последовательности. Ввиду корреляции между факторами значимость одного и того же фактора может быть разной в зависимости от последовательности его введения в модель. Мерой для оценки включения фактора в модель служит частный  F- критерий, т.е. .

                                                         (3.33)

Где 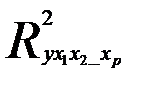- коэффициент множественной детерминации для модели с полным набором факторов;

   - тот же показатель, но без включения в модель фактора ;

          - число наблюдений;

            - число параметров в модели (без свободного члена).

 Если оцениваем значимость влияния фактора , то формула частного F –критерия примет вид:

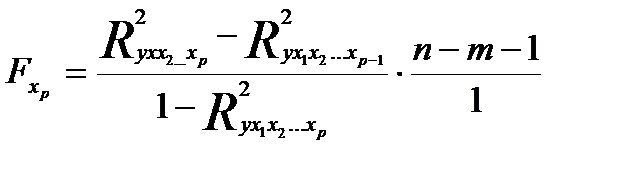                                               (3.34)

В общем виде для фактора частный -критерий определится как

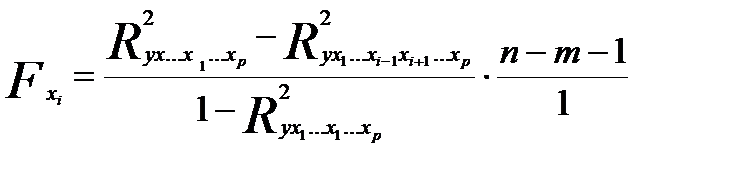
В числителе – прирост доли вариации у за счет дополнительный включается в модель соотношения фактура, в значении доля остаточных вариации для полной модели

 Рассмотреть зависимость объема продукции у от затрат труда х, и технической оснащенности производства .

Известны:

          .

 

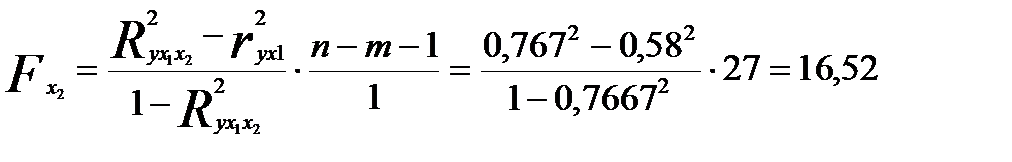
Дисперсионный анализ

 

Частный F-критерий оценивает значимость коэффициентов чистой регрессии. Зная величину F­_xi, можно определить и t-критерий для коэффициента регрессии при i-м факторе, t_bi, а именно:

                                         

Если уравнение содержит больше двух факторов, то соответствующая программа РС дает таблицу дисперсионного анализа, показывая значимость последовательного добавления к уравнению регрессии соответствующего фактора. Так, если рассматривается уравнение:

                      

то определяются последовательно F-критерий для уравнения с одним фактором х₁, далее F-критерий для дополнительного включения в модель фактора х₂, т.е. для перехода от однофакторного уравнения регрессии к двухфакторному, и наконец, F-критерий для дополнительного включения в модель фактора х­₃, т.е дается оценка значимости фактора х­₃  после включения в модель факторов х₁  и х₂. В этом случае F-критерий для дополнительного включения фактора х₂ после х₁ является последовательным в отличие от F-критерия для дополнительного включения фактора х_3­, который является частным F-критерием, ибо оценивает значимость фактора в предположении, что он включен в модель последним. С t-критерием Стьюдента связан именно частный F-критерий. Последовательный F-критерий может интересовать исследователя на стадии формирования модели.

Оценка значимости коэффициентов чистой регрессии по t-критерию Стьюдента может быть проведена и без расчета частных F-критериев. В этом случае, как и в парной регрессии, для каждого фактора используется формула:

                                

где b_{i ­} - коэффициент чистой регрессии при факторе х_i

  m_bi – стандартная ошибка коэффициента регрессии b_{i ­.}

Для уравнения множественной регрессии:

                      

стандартная ошибка коэффициента регрессии может быть определена по следующей формуле:

                        

- среднеквадратическое отклонение для признака у;

- среднеквадратическое отклонение для признака х_i

- коэффициент детерминации для уравнения множественнаой регрессии.

- коэффициент детерминации для значимости фактора х_i со всеми другими факторами уравнения множественной регрессии.

n – m – 1 - число степеней свободы для остаточной суммы квадратов отклонений.

Как видим, чтобы воспользоваться данной формулой, необходимы матрица межфакторной корреляции и расчет по ней соответствующих коэффициентов детерминации . Так, для уравнения

оценка значимости коэффициентов регрессии b₁, b₂, b₃ предполагает расчет трех межфакторных коэффициентов детерминации, а именно: , , .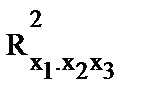

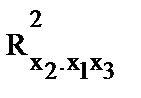Вместе с тем, если учесть, что

               

то можно убедиться, что

                             

На основе соотношения b_i   и m_bi получим

Аналогично можно оценивать и существенность частных показателей корреляции. Фактическое значение частного коэффициента корреляции сравнивается с табличным значением при   или  и числе степеней свободы k=n-h-2, где n - число наблюдений, h - число исключенных переменных. Так, если n =30 и оценивается существенность частного коэффициента корреляции второго порядка (например, ), то h=2 и k=26.

Если h является наивысшим порядком расчета частных коэффициентов корреляции для уравнения регрессии, то практически величина k совпадает с числом степеней свободы для остаточной вариации с n-m-1. Так, в уравнении , рассчитанном при n=30, n-m-1 =26. Если же уравнение регрессии дополняется расчетом частных коэффициентов корреляции разных порядков (второго, третьего и т.п.), то

k=n-h-2

Если величина частного F-критерия выше табличного значения, то это означает одновременного не только значимость рассматриваемого коэффициента регрессии, но и значимость частного коэффициента корреляции. Существует взаимосвязь между квадратом частного коэффициента корреляции и частным F-критерием, а именно:

Где   - частный коэффициент детерминации фактора  с y при неизменном уровне всех других факторов.

- доля остаточной вариации уравнения регрессии, включающего все факторы, кроме фактора  

- доля остаточной вариации для уравнения регрессии с полным набором факторов.

Пример. Для рассматриваемой регрессии

 ;     ;   

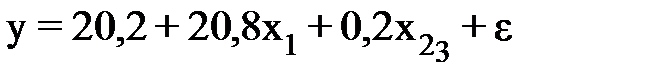
Тогда

что соответствует ранее определенной величине .

Взаимосвязь показателей частного коэффициента корреляции, частного F-критерия и t- критерия Стьюдента для коэффициентов чистой регрессии может использоваться в процедуре отбора факторов. Отсев факторов при построении уравнения регрессии методом исключения практически можно осуществлять не только по частным коэффициентам корреляции, исключая на каждом шаге фактор с наименьшим незначимым значением частного коэффициента корреляции, но и по величинам t_bi и F_xi. Частный F-критерий широко используется и при построении модели методом включения переменных и шаговым регрессионным методом.

Предыдущая1234567891011121314Следующая

Поделиться:

Воспользуйтесь поиском по сайту: