 |
Проблема гетероскедастичности. Её экономические причины и методы выявления.
|
|
|
|
В соответствии с третьей предпосылкой МНК требуется, чтобы дисперсия остатков была гомоскедастичной. Это значит, что для каждого значения фактора  остатки
остатки  имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность. Наличие гетероскедастичности можно наглядно видеть из поля корреляции (рис. 3.4).
имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность. Наличие гетероскедастичности можно наглядно видеть из поля корреляции (рис. 3.4).



Рис 3.4 примеры гетероскедастичности:
а – дисперсия остатков растет по мере увеличения x;
б – дисперсия остатков достигает максимальной величины при средних значениях переменной x и уменьшается при минимальных и максимальных значения x,
в – максимальная дисперсия остатков при малых значениях x и дисперсия остатков однородна по мере увеличения значений x
Гомоскедастичность остатков означает, что дисперсия остатков  одинакова для каждого значения х. используя трехмерное изображение, получим следующие графики, иллюстрирующие гомо- и гетероскедастичность (рис. 3.5, 3.6).
одинакова для каждого значения х. используя трехмерное изображение, получим следующие графики, иллюстрирующие гомо- и гетероскедастичность (рис. 3.5, 3.6).
F( ) )
|
| 0 |

|

|

|
| x |
Рис.3.5. Гомоскедастичность остатков
F( ) )
|
| 0 |

|

|
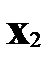
|

|
| x |
Рис. 3.6. Гетероскедастичность остатков
Рис.3.5 показывает, что для каждого значения  распределения остатков
распределения остатков  одинаковы в отличие от рис. 3.6, где диапазон варьирования остатков меняется с переходом от одного значения
одинаковы в отличие от рис. 3.6, где диапазон варьирования остатков меняется с переходом от одного значения  к другому. Соответственно на рис. 3.6. демонстрируется неодинаковая дисперсия
к другому. Соответственно на рис. 3.6. демонстрируется неодинаковая дисперсия  при разных значениях
при разных значениях  .
.
Наличие гомоскедастичности или гетероскедастичности можно видеть и по рассмотренному выше графику зависимости остатков  от теоретических значений результативного признака
от теоретических значений результативного признака  . Так, для рис.3.4 а) зависимость остатков от
. Так, для рис.3.4 а) зависимость остатков от  представлена на рис.3.7.
представлена на рис.3.7.
|
|
|

Рис.3.7. Гетероскедастичность: большая дисперсия  для больших значений
для больших значений 
Соответственно для зависимости, изображенной на полях корреляции рис. 3.4 б) и в), гетероскедастичность остатков представлена на рис. 3.8 и 3.9.
Для множественной регрессии данный вид графиков является наиболее приемлемым визуальным способом изучения гомо- и гетероскедастичности.

Рис. 3.8. Гетероскедастичность, соответствующая полю корреляции рис. 3.4 б)
Рис.3.9. Гетероскедастичность, соответствующая полю корреляции рис. 3.4 в)
Наличие гетероскедастичности может в отдельных случаях привести к смещенности оценок коэффициентов регрессии, хотя несмещенность оценок коэффициентов регрессии в основном зависит от соблюдения второй предпосылки МНК, т. е. независимости остатков и величин факторов. Гетероскедастичность будет сказываться на уменьшении эффективности оценок  . В частности, становится затруднительным использование формулы стандартной ошибки коэффициента регрессии
. В частности, становится затруднительным использование формулы стандартной ошибки коэффициента регрессии  , предполагающей единую дисперсию остатков для любых фактора. Практически при нарушении гомоскедастичности мы имеем неравенства:
, предполагающей единую дисперсию остатков для любых фактора. Практически при нарушении гомоскедастичности мы имеем неравенства:




 , j
, j  I,
I, 
и можно записать



При этом величина  может меняться при переходе от одного значения фактора
может меняться при переходе от одного значения фактора  к другому. Это означает, что сумма квадратов отклонений для зависимости
к другому. Это означает, что сумма квадратов отклонений для зависимости
 =
=  a+b·x
a+b·x
При наличии гетероскедастичности должна иметь вид:
 =
=  .
.
При минимизации этой суммы квадратов отдельные ее слагаемые взвешиваются: наблюдениям с наибольшей дисперсией придается пропорционально меньший вес. Иными словами, вклад каждого сочетания  с
с 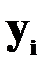 в сумму квадратов остатков должен быть дисконтирован, чтобы учесть систематическое влияние неоднородных элементов
в сумму квадратов остатков должен быть дисконтирован, чтобы учесть систематическое влияние неоднородных элементов  .
.
Задача состоит в том, чтобы определить величину  и внести поправку в исходные переменные. С этой целью рекомендуется использовать обобщенный метод наименьших квадратов, который эквивалентен обыкновенному МНК, примененному к преобразованным данным. Чтобы убедиться в необходимости использования обобщенного МНК, обычно не ограничиваются визуальной проверкой гетероскедастичности, а проводят ее эмпирическое подтверждение.
и внести поправку в исходные переменные. С этой целью рекомендуется использовать обобщенный метод наименьших квадратов, который эквивалентен обыкновенному МНК, примененному к преобразованным данным. Чтобы убедиться в необходимости использования обобщенного МНК, обычно не ограничиваются визуальной проверкой гетероскедастичности, а проводят ее эмпирическое подтверждение.
|
|
|
Гетероскедастичность становится проблемой, когда значения переменных, входящих в уравнение регрессии, значительно различаются в разных наблюдениях. Если истинная зависимость описывается уравнением у = а +  +
+  и переменные меняют свой масштаб одновременно, то изменения значений не включенных переменных и ошибки измерения, влияя совместно на случайную составляющую, делают его сравнительно малым при малых у и x и сравнительно большим при больших у и х. Пусть рассматривается зависимость между государственными расходами на образование и валовым внутренним продуктом в различных странах. Доля государственных расходов на образование составляет обычно 3-9% от ВВП. Очевидно, что если одновременно включить в выборку данные как по малым странам, таким как Люксембург, и большим, таким как Россия, то цифры будут несоотносимыми. Правда, из такой ситуации просто найти выход – вместо расходов на образование в их численном эквиваленте можно исследовать долю этих расходов в ВВП соответствующей страны. Также гетероскедастичность может проявиться при анализе данных, которые увеличиваются со временем. Например, при исследовании зависимости спроса от доходов населения очевидно, что как доходы, как и цены на товары и услуги могли просто возрасти со временем, и дисперсия случайной составляющей тоже может со временем увеличиваться.
и переменные меняют свой масштаб одновременно, то изменения значений не включенных переменных и ошибки измерения, влияя совместно на случайную составляющую, делают его сравнительно малым при малых у и x и сравнительно большим при больших у и х. Пусть рассматривается зависимость между государственными расходами на образование и валовым внутренним продуктом в различных странах. Доля государственных расходов на образование составляет обычно 3-9% от ВВП. Очевидно, что если одновременно включить в выборку данные как по малым странам, таким как Люксембург, и большим, таким как Россия, то цифры будут несоотносимыми. Правда, из такой ситуации просто найти выход – вместо расходов на образование в их численном эквиваленте можно исследовать долю этих расходов в ВВП соответствующей страны. Также гетероскедастичность может проявиться при анализе данных, которые увеличиваются со временем. Например, при исследовании зависимости спроса от доходов населения очевидно, что как доходы, как и цены на товары и услуги могли просто возрасти со временем, и дисперсия случайной составляющей тоже может со временем увеличиваться.
При наличии такой ситуации используют обобщенный МНК, который будет рассмотрен ниже. Чтобы убедиться в необходимости применения этого метода, визуальной проверки гетероскедастичности недостаточно, необходима формальная проверка. Существует большое количество разнообразных тестов.
Если предполагается, что дисперсия случайной составляющей будет либо увеличиваться, либо уменьшаться по мере увеличения x, можно применить тест ранговой корреляции Спирмена. Данные по x и остатки упорядочиваются, и коэффициент ранговой корреляции определяется как:
 =1-
=1-  ,
,
Где  - разность между рангом x и рангом
- разность между рангом x и рангом 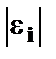 .
.
|
|
|
Если предположить, что соответствующий коэффициент корреляции для генеральной совокупности равен нулю, то коэффициент ранговой корреляции имеет нормальное распределение с M=0 и 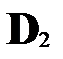 =
=  в больших выборках. Соответствующая тестовая статистика будет равна
в больших выборках. Соответствующая тестовая статистика будет равна 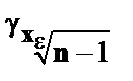 , и гипотеза об отсутствии гетероскедастичности будет отклонена при уровне значимости в 5%, если она превысит 1,96 и при уровне значимости в 1%, если она превысит 2,58. Если в модели несколько объясняющих переменных, гипотезы может выполняться с использованием любой из них.
, и гипотеза об отсутствии гетероскедастичности будет отклонена при уровне значимости в 5%, если она превысит 1,96 и при уровне значимости в 1%, если она превысит 2,58. Если в модели несколько объясняющих переменных, гипотезы может выполняться с использованием любой из них.
При малом объеме выборки, что наиболее характерно для эконометрических исследований, для оценки гетероскедастичности может использоваться метод Гольдфельда – Квандта, разработанный в 1965 г. Гольдфельд и Квандт рассмотрели однофакторную линейную модель, для которой дисперсия остатков возрастает пропорционально квадрату фактора. Чтобы оценить нарушение гомоскедастичности, они предложили параметрический тест, который включает в себе следующие шаги.
1. Упорядочение n наблюдений по мере возрастания переменной x.
2. Исключение из рассмотрение. С центральных наблюдений; при этом
(n-C):2  p, где p – число оцениваемых параметров.
p, где p – число оцениваемых параметров.
3. Разделение совокупности из (n-C) наблюдений на две группы (соответственно с малыми и большими значениями фактора x) и определение по каждой из групп уравнений регрессии.
4. Определение остаточной суммы квадратов для первой ( ) и второй (
) и второй ( ) групп и нахождение их отношения:
) групп и нахождение их отношения:  =
=  :
:  .
.
При выполнении нулевой гипотезы о гомоскедастичности отношение  будет удовлетворять F-критерию с (n-C-2p):2 степенями свободы для каждой остаточной суммы квадратов. Чем больше величина
будет удовлетворять F-критерию с (n-C-2p):2 степенями свободы для каждой остаточной суммы квадратов. Чем больше величина  превышает табличное значение F-критерия, тем более нарушена предпосылка о равенстве дисперсий остаточных величин.
превышает табличное значение F-критерия, тем более нарушена предпосылка о равенстве дисперсий остаточных величин.
Рассмотрим решение следующей задачи.
Задача о поступлении доходов в консолидированный бюджет Санкт-Петербурга ( млрд.руб) в зависимости от численности работающих на крупных и средних предприятиях (х – тыс.чел.). Таблица 3.7
млрд.руб) в зависимости от численности работающих на крупных и средних предприятиях (х – тыс.чел.). Таблица 3.7
|
|
|
| № п/п | Районы города | 
| 
| 
| 
|
| 1 | Павловский | 3 | 4,4 | -1,0 | 5,4 |
| 2 | Кронштадт | 6 | 8,1 | 2,5 | 5,6 |
| 3 | Ломоносовский | 8 | 12,9 | 4,9 | 8,0 |
| 4 | Курортный | 18 | 20,8 | 16,6 | 4,2 |
| 5 | Петродворец | 20 | 15,5 | 19,0 | - 3,5 |
| 6 | Пушкинский | 23 | 28,8 | 22,5 | 6,3 |
| 7 | Красносельский | 39 | 37,5 | 41,4 | - 3,9 |
| 8 | Приморский | 49 | 48,7 | 53,2 | -4,5 |
| 9 | Колпинский | 60 | 68,6 | 66,1 | 2,5 |
| 10 | Фрунзенский | 74 | 104,6 | 82,6 | 22,0 |
| 11 | Красногвардейский | 79 | 90,5 | 88,5 | 2,0 |
| 12 | Василеостровский | 95 | 88,3 | 107,4 | -19,1 |
| 13 | Невский | 106 | 132,4 | 120,4 | 12,0 |
| 14 | Петроградский | 112 | 122,0 | 127,4 | -5,4 |
| 15 | Калининский | 115 | 99,1 | 131,0 | -31,9 |
| 16 | Выборгский | 125 | 114,2 | 142,7 | - 28,5 |
| 17 | Кировский | 132 | 150,6 | 151 | - 0,4 |
| 18 | Московский | 149 | 156,1 | 171 | - 14,9 |
| 19 | Адмиралтейский | 157 | 209,5 | 180,5 | 29,0 |
| 20 | Центральный | 282 | 342,9 | 327,8 | 15,1 |
| Итого | 1652 | 1855,5 | 1855,5 | 0 |
 Рассмотрим табл. 3.7.
Рассмотрим табл. 3.7.
В соответствии с уравнением



Найдены теоретические значения  и отклонения от них фактических значений y, т. е.
и отклонения от них фактических значений y, т. е.  .
.
Итак остаточные величины  обнаруживают тенденции к росту по мере увеличения x и y (рис.3.10).
обнаруживают тенденции к росту по мере увеличения x и y (рис.3.10).


Рис.3.10. График остатков для примера по табл. 3.7
Этот вывод подтверждается и по критерию Гольдфельда – Квандта. Для его применения необходимо определить сначала число исключаемых центральных наблюдений С. Из экспериментальных расчетов, проведенных авторами метода для случая одного фактора, рекомендовано при n=30 принимать С=8, а при n=60 – соответственно С=16. в рассматриваемом примере при n=20 было отобрано С=4. Тогда в каждой группе будет по 8 наблюдений [(20-4):2]. Результаты расчетов представлены в табл. 3.8.
Таблица 3.8
Проверка линейной регрессии на гетероскедастичность
| Уравнения Регрессии | Х | У | 
| 
| 
|
Я группа с
Первыми 8
районами:
 =2,978+0,921х
=2,978+0,921х
Я группа с
Последними
8 районами:
 =31,142+1,338х
=31,142+1,338х


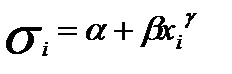
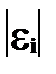 и оценивают их регрессию на
и оценивают их регрессию на  для данного значения с, после оценивается статистическая значимость коэффициента b.
для данного значения с, после оценивается статистическая значимость коэффициента b. распределены независимо друг от друга. Автокорреляция остатков означает наличие корреляции между остатками текущих предыдущих (последующих) наблюдений. Коэффициент корреляции между
распределены независимо друг от друга. Автокорреляция остатков означает наличие корреляции между остатками текущих предыдущих (последующих) наблюдений. Коэффициент корреляции между  и
и  , где
, где  -остатки текущих наблюдений,
-остатки текущих наблюдений, 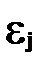 - остатки предыдущих наблюдений (например, j= i -1), может быть определен как
- остатки предыдущих наблюдений (например, j= i -1), может быть определен как ,
,
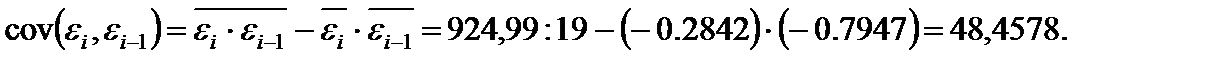
 получим:
получим: =0,2168, что при 17 степенях свободы явно незначимо (F-отношение<1) и демонстрирует отсутствие автокорреляции остатков.
=0,2168, что при 17 степенях свободы явно незначимо (F-отношение<1) и демонстрирует отсутствие автокорреляции остатков.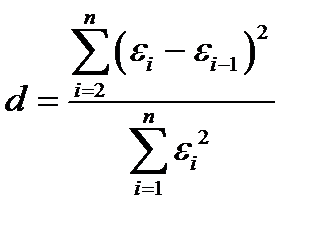
 , т.е. величина случайной составляющей в любом наблюдении равна ее значению в предшествующем наблюдении, множенному на p, плюс новая ошибка е, то если известна величина p, можно полностью устранить автокорреляцию. Например, пусть рассматриваем уравнение вида (1) (при нескольких факторах принцип будет тот же). Наблюдения n и n-1 соответственно равны:
, т.е. величина случайной составляющей в любом наблюдении равна ее значению в предшествующем наблюдении, множенному на p, плюс новая ошибка е, то если известна величина p, можно полностью устранить автокорреляцию. Например, пусть рассматриваем уравнение вида (1) (при нескольких факторах принцип будет тот же). Наблюдения n и n-1 соответственно равны: , должно быть некоррелированным с ее значением в предыдущем наблюдении. В экономическом анализе чаще всего встречается положительная автокорреляция. Предположим, оценивается зависимость спроса на мороженое от дохода и что неучтенным фактором, «скрытым» в
, должно быть некоррелированным с ее значением в предыдущем наблюдении. В экономическом анализе чаще всего встречается положительная автокорреляция. Предположим, оценивается зависимость спроса на мороженое от дохода и что неучтенным фактором, «скрытым» в 

