Классическое и квантовое описание системы

Экспериментальные основы квантовой механики

1900г. Планк ввел понятие о квантах и ввел квантовую постоянную. Работа Планка объясняла теорию излучения твердых тел.

1905г. Классификация спектров Ритцем и Ридбергом. Все спектральные линии могут быть посчитаны через термы , где - постоянная Ридберга, n – натуральное число.

1913г. Н. Бор теоретически объяснил спектр атома водорода (постулаты Бора).

Эксперименты Франка и Герца. Они рассматривали неупругое рассеяние электронов на атомах. Пропускали пучки электронов через пары ртути. При определенных энергиях, электроны при соударении с атомами ртути теряли часть своей энергии.

 

 

 

Установка:

Была показана энергетическая дискретность атома ртути, определены энергетические уровни:

1922г. Опыты Штерна и Герлаха по расщеплению атомного пучка в неоднородном магнитном поле.

По оси z поле в обкладках магнита неоднородно. Так как есть градиент поля , то если пропускать вдоль оси x частицы, имеющие магнитный момент , то возникает сила:

Наблюдалось расщепление атомного пучка. С точки зрения классической теории все 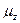равновероятны и поэтому должна получиться одна широкая полоса. Наблюдались две четкие линии.

Подтвердили, что магнитный момент атома квантуется, т. е. принимает дискретные значения.

,

где для серебра.

 

1923 – 1924 гг. Теория Де Бройля корпускулярно-волнового дуализма частиц. Соотношения теории:

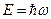
Здесь слева параметры частицы: энергия и импульс. Справа параметры волны: частота, волновой вектор.

Волна Де Бройля:

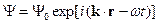
, - длина волны Де Бройля.

 

1927г. Дэвиссон и Джермер. Рассеяние электронов на кристаллической решетке. Подтверждение волновых свойств частиц.

Классическое и квантовое описание системы

Опыт № 1. Имеется источник частиц, экран с достаточно узким отверстием. Картину наблюдаем на Э2

Опыт № 2. Заменяем Э1 на Э1^/.

Опыт № 3. Объединяем экраны Э1 и Э1^/

При классическом описании опыт 3 давал бы сложение интенсивностей от опыта 1 и 2. Однако опыт 3 показал интерференционную картину, а это волновые свойства. Частица с определенной вероятностью проходит как через щель 1 так и через щель 2. Нельзя точно сказать через какую щель пройдет электрон. Классическая интерпретация (с числом степеней свободы n=1) решается составлением уравнений в форме Гамильтона:

 

Можно найти траекторию частицы. В общем случае состояние механической системы определяется динамическими переменными, т.е. начальных условий. Но опыт показал, что мы не можем определить траекторию частицы в микромире. Количество динамических переменных, которые могут быть одновременно измерены в микромире, в квантовой механике – n.

 

Скорость

Координата

Если известна точка , то чтобы найти положение точки надо знать и одновременно, т. е. координаты и импульс должны быть измерены одновременно. Если мы знаем и , то можем построить траекторию электрона. Однако построить такую траекторию мы не можем (опыт № 3). Тогда мы не можем одновременно измерить p и q.

[§3.] Принцип неопределенности

Две формулировки:

1) В микромире понятие “траектория” отсутствует

2) Канонически сопряженные величины одновременно неизмеримы

В трехмерном пространстве канонически сопряженные величины будут:

p_x и x

p_y и y

p_z и z

Здесь n=3. Имеем 3 одновременно измеряемые динамические переменные. Например:

1) p_x. p_y. p_z

2) x, y, z

3) x, y, p_z и тд.

 

[§4.] Полный набор динамических переменных

Полный набор динамических переменных – это наибольший набор независимых одновременно измеримых динамических переменных. Измерение полного набора динамических переменных полностью определяет состояние квантово-механической системы. Число динамических переменных в квантовой системе - n и по сравнению с классической системой (2n) уменьшается в 2 раза. Максимальный набор – это значит, что к этому набору не может быть добавлена ни одна другая переменная, которая не являлась бы их функцией. В этом случае они не зависимы. Каждая из этих переменных не является функцией другой переменной из этого же набора. Заметим, что здесь зависимость не линейная (как в линейной алгебре), а функциональная.

 

[§5.] Постулаты квантовой механики

Часто выделяют 4 постулата:

1) Постулат о волновой функции.

Каждой системе (состоянию кв.-мех. системы) может быть поставлена в соответствие волновая функция динамических переменных (из полного набора) и времени, полностью описывающей состояние системы.

Динамические переменные одновременно измеримы. - n – мерный вектор динамических переменных; функция динамических переменных и времени - описывает эволюцию квантово-механических систем. классической механике задание 2n динамических переменных полностью определяет состояние системы через функцию Гамильтона. В квантово-механической системе описывается эволюция системы через - функцию от n динамических переменных.

2) О связи физических величин и объектов математики (операторов).

Каждой физической величине (наблюдаемой) ставится в соответствие оператор:

3) Связь между результатами измерения физической величины и значением оператора (т. е. решением математических задач)

Пусть 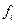- значение физической величины , которое получено в результате измерения системы, находящейся в i -том квантовом состоянии.

является одним из собственных значений оператора . Это задача на собственные функции и собственные значения. Задача определяет собственные значения , соответствующие и определяет собственные функции , соответствующие собственным значениям . Если собственные значения образуют дискретное множество, то говорят о дискретном спектре. Если собственные значения образуют непрерывное множество, то спектр непрерывный.

4) Определение среднего значения физической величины

Здесь введено понятие скалярного произведения для функций из гильбертова пространства. Гильбертово пространство – это пространство квадратично интегрируемых функций (нормируемых функций). Если 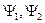- квадратично интегрируемые функции, тогда:

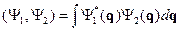
Это определение для - декартовых переменных. Для перехода к другой системе координат вводится якобиан перехода. Значок «*» означает комплексное сопряжение.

Это аналог длины в векторном пространстве.

 

1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: