Определение запаса устойчивости исходной САУ

Устойчивость замкнутой САУ удобнее всего оценивать по ПФ разомкнутой системы с помощью логарифмического критерия Найквиста. Для этого необходимо построить ЛХЧ разомкнутой системы. В Control System Toolbox для расчета ЛХЧ применяются две функции bode и mаrgin. Удобнее использовать последнюю, т.к. результатом её выполнения является не только графики ЛЧХ, но и численные значения запаса по фазе Р_m, частоты среза и запаса по амплитуде G_m.

Применим функцию mаrgin для исследования запаса устойчивости рассматриваемого варианта следящей системы:

 

>> margin (W); grid on

 

Здесь команда grid on использована для нанесения сетки на график. В результате получаются ЛЧХ, представленные на рис. 6.1. Из них видно, что система имеет очень малый запас по фазе 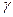= P_m=13°, т.е. замкнутая САУ устойчива, но находится близко к границе устойчивости.

Рис. 6.1. ЛЧХ разомкнутой САУ

 

Следует отметить, что в удовлетворительно спроектированных системах запас по фазе лежит обычно в диапазоне 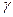= 45 ÷ 70°.

 

Оценка динамических показателей качества исходной САУ

К динамическим показателям качества относят перерегулирование и длительность переходного процесса t_п, которые определяются из переходной характеристики замкнутой САУ. Для построения данной характеристики в Control System Toolbox применяется функция step, аргументом которой является передаточная функция замкнутой системы

 

Ф(s)=

где W ₁(s) – передаточная функция прямого канала САУ,

W ₀(s) – ПФ цепи обратной связи.

 

Для получения Ф(s) можно воспользоваться функцией feedback (W₁,W₀). Для рассматриваемого примера имеем W ₁(s) = W(s), W ₀(s) =1 и соответственно:

 

>> F=feedback (W,1)

 

Transfer function:

1.584

---------------------------------------------------------------------------------------------------

2.88e-005 s^6 + 0.00529 s^5 + 0.08456 s^4 + 0.5012 s^3 + 1.206 s^2 + s + 1.584

 

Далее можно рассчитать переходную характеристику с помощью функции step:

 

>> step (F); grid on

 

В результате получим искомый график, представленный на рис. 6.2. В данном случае получился сходящийся колебательный процесс, что подтверждает устойчивость исходной следящей системы с малым запасом по фазе γ =13°.

 

Рис. 6.2. Переходная характеристика замкнутой САУ

Из переходной характеристики с помощью известных в теории автоматического управления способов определяются два основных динамических показателя качества:

· перерегулирование ,

где , 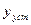– соответственно максимальное и установившееся значения выходной координаты;

· – длительность переходного процесса, которая равна интервалу времени, за который кривая переходной характеристики входит в зону (0,95÷1,05) y_уст, в дальнейшем не выходя из неё.

Анализ полученной переходной характеристики (рис. 6.2), показывает, что =70%, =23.3 с. Это говорит о неудовлетворительном качестве динамических процессов в следящей системе: перерегулирование в реальных САУ лежит в диапазоне = 10 ÷ 30%, а сравнимо с максимольной постоянной времени контура управления (в нашем случае Т_К = 0.5 с).

В заключение по результатам анализа исходной САУ делается общий вывод. Практически во всех случаях систему требуется корректировать. Во-первых, если система обладает заданной точностью, то она, как правило, неустойчива или имеет малый запас устойчивости. В последнем случае динамические показатели качества также получаются не совсем приемлемыми (значительная колебательность, большая величина перерегулирования ). Во-вторых, если САУ имеет низкую точность, то система обычно устойчива, но качество динамики САУ оставляет желать лучшего – при приемлемом получается очень большое время .

 

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: