 |
Основные термодинамические процессы
|
|
|
|
Идеального газа
При анализе любого термодинамического процесса стремятся установить характер зависимости между параметрами в ходе процесса, способы его графического отображения, а также определить характер энергетических преобразований, количество теплоты и работы, и получить соотношение для вычисления изменения внутренней энергии, энтальпии и энтропии.
Таким образом, анализируя термодинамические процессы, рассматривают изменение трех функций состояния (u, h,s) и двух функций процесса (удельной теплоты q и работы ℓ), значения которых зависят от вида процесса.
Основными, или частными, термодинамическими процессами называют процессы, совершающиеся при постоянном значении одного из термических
Параметров или при условии равенства нулю одного из составляющих первого закона термодинамики.
Различают следующие термодинамические процессы: изохорный (V = const); изобарный (Р = const); изотермический (Т = const); процесс, протекающий без обмена теплотой между рабочим телом и окружающей средой (dq=const; S =const), так называемый изоэнтропный, или адиабатный.
Общий случай представляют политропные процессы, характеризующиеся постоянством теплоёмкости.
Законы идеального газа
Законы идеального газа были установлены эмпирическим путем.
Закон Бойля- Мариотта: при постоянной температуре произведение давления газа на его объём есть величина постоянная, т.е. при T =const PV = const.
Закон Гей-Люсака: при постоянном давлении удельный объём газа изменяется прямо пропорционально его термодинамической температуре, т.е. при p = const,
v1/v2 = T1 /T2.
Если применить оба выше рассмотренных закона к любому процессу, то получим соотношение
|
|
|
p1v1/T1 = p2v2/T2, или pv /T = const. (3.1).
Постоянная величина в правой части выражения (3.1)
Зависит от свойств газа и для каждого газа имеет своё значение. Её называют газовой постоянной R:
PV = RT (3.2).
Это уравнение однозначно связывает термические параметры p,v, T (рис. 3.1) и является уравнением состояния идеального газа (уравнение Клапейрона).
Закон Авагадро: в равных объёмах газов, по свойствам близким к идеальному газу, при одинаковых давлении и температуре содержится равное число молекул.
Рисунок 3.1. Зависимости между параметрами состояния
идеального газа.
Согласно закону Авагадро 1 Кмоль любого идеального газа при нормальных условиях содержит одинаковое число молекул и называется числом Авагадро NA =6,022169· 1026 кмоль-1. Молярный объём 1 кMоля равен 22,42 м3.
Если обе части уравнения (3.2) умножим на молярную массу М, то получим уравнение Клапейрона – Менделева.
p·v·M =MRT, или pVM = RMT pvm =RTm, (3.3).
где — R - универсальная газовая постоянная RM =pVM/T для всех
газов, находящихся в состоянии, близком к идеальному, и равна
RM = 8,3143 Дж/(моль*К); где- m – масса газа, кг.
Изохорный процесс
В общем виде основное уравнение изохорного процесса
p = f1(v=const; T ). Рассматривая уравнение Клапейрона (3.2) для идеального газа в состоянии 1 и 2, и учитывая уравнение изохоры v1=v2 =const, получим соотношение параметров для изохорного процесса:
1. p2 /p2 =T2 /T1. (3.4). 2. Поскольку объём постоянен, т.е. dv = 0, то работа изменения объёма равна нулю
( l1-2= 
). Удельная техническая работа lTEX = - v(p2 – p1) (пл.1-2, p1/ p2 рис3.2) Из общего уравнения первого закона термодинамики (разд. 2). количество теплоты, подведенное в изохорный процесс, полностью затрачивается на изменение внутренней энергии, т.е. при dv = 0 δq = du qV1-2 =u2 (v2T2) – u1(v1T1 ) отсюда
u2 (v2T2) – u1(v1T1) = 
(3.5).
поэтому dq = C vd T, qV1-2 = cV (T2 – T1).
3. Изменение энтропии в процессе определим из соотношения ds = dq/T = CV dT; интегрируя его, получим
s2 – s1= CVln (T2/T1 ) (3.6).
|
|
|
На T-S диаграмме линия V = const изображается логарифмической кривой процесса (рис. 3.2).
Р Т 2
Р2 1 1 qV1-2
l ТЕХ
Р1 2
0 V 0 S1 S2 S
Рисунок 3.2. График изохорного процесса
Пример 3.1. В баллоне емкостью 15 л содержится воздух при давлении 0,4 МПа и температуре 300 С. Какова будет температура воздуха в результате подвода к нему
16 кДж теплоты? Удельная изохорная теплоемкость Cvm = 717 Дж/(кг.К); газовая постоянная R = 287,1 Дж/(кгК).
Р е ш е н и е. 1. Предварительно вычислим массу воздуха m по формуле (3.3)
m = p1 V/ (RT1) = 0,4*106 *0,015/(287,1*303)=0,069 кг.
2. Найдем конечную температуру t2 из уравнения (3.5)
Q1,2 = mcvm (t2 – t1) откуда
t2 = t1 +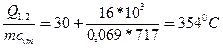 
Изобарный процесс
Общее уравнение изобарного процесса v = f(T, p =const).
1. Из равенства P1 ·V1 = RT1 и P2·V2 = RT2 получим
, удельный объем v возрастает при подведении теплоты и уменьшается при охлаждении рабочего тела.
2. Удельная работа в процессе (на P – V диаграмме пл. 1,2v2 v1)
l1-2 = p(v2 - v1) = R(T2 – T1), (3.9). техническая работа ℓTEX = - 
= 0
p
1 lP1-2 2 dℓ = pdv; ℓ= 
=p(v2 – v1)
0 V1 V2 V
Удельное количество теплоты определяем из первого закона т/динамики:δq = dh. Количество теплоты в изобарном процессе равно изменению энтальпии
рабочего тела qp2-1 = h2 –h1 (на T-S диаграмме пл. 12S2S1).
T
V =const 1
Т2 2
 |
Т1 P = const
S
0 S1 S2
3.Изменение внутренней энергии равно
Δu = CV (T2 – T1); CV ≠ f (T)
4. Изменение энтальпии Δh = CP (T2 – T1); CP ≠ f (T)
5. Изменение энтропии в изобарном процессе
s2(p;T2) - S1(p; T1) = 
(3.8).
Если в интервале Т1……Т2 теплоемкость СР постоянна, то
S2 – S1 = CР· ln(T2 – T1)
Изобара на Т-S диаграмме изображается логарифмической кривой. Если СP>CV, то при одинаковом изменении температуры ΔSP>S V, следовательно, на Т-S диаграмме изобара располагается более полого, чем изотерма.
Пример 3.2. Азот массой 0,5 кг расширяется по изобаре при абсолютном давлении 0,3 МПа так, что его температура повышается от 100 до 3000С.
Найти конечный объём азота, совершенную работу и подведенную теплоту. Удельная газовая постоянная R = 296,8 Дж/(кг.К).
Р е ш е н и е. 1. Находим начальный объем азота из уравнения (3.5):
V1 = mRT1/p1 =0,5*296,8*373/(0,3*106) = 0,184 м3
2. Теперь найдем конечный объем:
V2 = V1*T1/T2 =0,184*573/373 = 0,284 м3.
3. Определим работу изменения объёма (уравнение 3.7)
L1,2=p (V2 – V1) = 0,3*106 (0.287- 0.184)= 30*103 Дж
4. Работа изменения давления l ТЕХ = 0.
|
|
|
5. Определим теплоту, подведенную к газу по уравнению
Q1,2 = mcpm(t2 – t1), заменяя Т2-Т1 на t2 -t1
При средней температуре tm (t1 + t2)/2 = 200ОС
средняя удельная изобарная теплоемкость азота равна
Cpm = Cpm/M=29, 38*103/28,02 = 1047 Дж/(кгК)
Таким образом,
Q1,2=0,5*1047(300-100)=104,7*103 Дж.
|
|
|
