 |
Изотермический процесс
|
|
|
|
Процесс осуществляется по изотерме при T = const.
В общем случае в ходе процесса изменяются давление p и удельный объём v. Общее уравнение p = f(v;T=cоnst).
Для идеального газа на изотерме давление и объём связаны уравнением pv = const. На p – v диаграмме изотерма изображается равнобокой гиперболой 1 – 2
Изотермы реальных веществ имеют более сложный характер, но так как у любых веществ величина (dv/dp)T всегда отрицательна, то на изотерме везде с увеличением давления уд. объём уменьшается.
Р V1
1
V2
l1-2 2
0 V
 |
Т
q1-2
 |
0 S1 S2 S
1. Работа изменения объёма в изотермическом процессе
Используя уравнение Клапейрона, выражение для этой работы в изотермическом процессе можно получить в таком виде:
l 1-2 = RT ln (p1/p2) = p1v1 ln(v2/v1) = p1v1ln(p1/p2). (3.9).
Удельная техническая работа 
Количество теплоты в процессе можно определить, исходя из общего состояния dq = Tds. Так как T =const, то
q1-2 = T(S2 - S1), (3.10).
что справедливо для всех газов и паров.
Изменение внутренней энергии и энтальпии тела
du=CvdT=0, dh=CPdT=0.
На T-S диаграмме процесс изображается прямой линией, располагаемой горизонтально. Удельная работа равна по. 1,2S2S1. Если энтропия возрастает – теплота подводится к телу и газ расширяется, если убывает – газ сжимается и теплота отводится.
Изменение энтропии в процессе для реального газа
S2(p2 T) – S1(p1T) = 
(3.11).
Для идеального газа S2 – S1=R·ln(v2- v1). (3.12).
Так как в этом процессе подвод теплоты к системе не приводит к изменению температуры, то теплоемкость в нем бесконечно велика. В изотермическом процессе вся подведенная теплота преобразуется в работу изменения объёма и сам процесс оказывается наиболее эффективным. С учетом, что du =0 следует,что dq = d l = pdv.
|
|
|
Пример 3.3. В компрессоре сжимается воздух массой 2 кг при постоянной температуре 2000С от p1 = 0,1 МПа до р2=2,5 МПа. Найти массу воды mВ, необходимую для охлаждения сжимаемого воздуха, если начальная температура воды 150С, а конечная 500С, удельная теплоемкость воды СВ = 4,19 кДж/(кг0С); RВОЗ.=287,1 Дж/(кгК)
Р е ш е н и е. 1. Найдем работу сжатия L1,2:
L1,2 = 2,3m*RТ l g (p1/p2)= 2,3*2*287,1*473*lg(0,1/2,5) = -2,3*2*287,1*473*1,398=
=- 866*103 Дж.
2. Так как в изотермическом процессе Q1,2= L1,2, то Q1,2= - 866 кДж и
Q1,2= mвсв(t˝в - t΄в), из этого уравнения
mВ= 
Адиабатный процесс
Основное условие адиабатного процесса dq = 0 или q = 0, т.е. в адиабатном процессе теплота к системе не подводится и не отводится от неё.
Однако в реальных условиях невозможно обеспечить условия, при которых теплообмен полностью исключен. Но применяя эффективную изоляцию рабочего тела от внешней среды можно свести к минимуму теплообмен и потерями тепла можно пренебречь. Например, процесс сжатия осуществляется настолько быстро, что теплоотдача не оказывает какого либо воздействия на его ход. Такой процесс можно считать адиабатным.
P T 1
1 s = const
q = const =0
T = const
2 2
0
V1 V2 V 0 S
Связь между параметрами процесса следующая
1. Уравнение самого процесса
q = 0; PVK = const, (3.13).
где К – показатель адиабаты, равный 
2. Связь между параметрами
; 
(3.14).
Изменение внутренней энергии
ΔU = CV (T2 – T1) = 
Vm 
(3.15).
2. Энтальпия
Δi = CP(T2 – T1) = Pm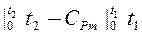 
(3.16). 3. Механическая работа
(3.17).
6. Теплоёмкость процесса 
(3.18).
7. Изменение энтропии.
ΔS = q/T = 0; S2 – S1 = const
Адиабатный процесс называют ещё изоэнтропным процессом.
Пример 3.4. Воздух массой 2 кг при давлении р 1 = 1МПа и температуре
t1 = 3000С расширяется по адиабате так, что его объем увеличивается в 5 раз.
Найти конечный объём, давление, температуру, работу изменения объема и изменение внутренней енергии. Принимаем R = 286,7 Дж/(кг·К).
Р е ш е н и е. 1. Находим начальный объём газа V1
|
|
|
V1 = mRT1/р1= 2*286,7*573/(1*106) = 0,33 м3.
По условию конечный объём V2=5 V1, поэтому
V2=5 · 0,33 = 1,65 м3.
2. Находим конечное давление р 2 из уравнения
Р1/Р2 = (V2/V1)k
Примем для воздуха значение показателя адиабаты
k = 1,4, как для смеси двухатомных газов, тогда Р1/Р2 = 51,4 = 9,96.
Отсюда р2 = р1/9,96=1·106/9,96 ≈ 0,1МПа. Из уравнения состояния (3.3) найдем конечную температуру Т2=p2V2/ mR =0,1·106·1,65/(2·287,1) = =288 К или
t2 = 288-273=150С.
Для вычисления работы L1,2 используем уравнение (3.17) в упрощенном виде
L1,2 =m·R(t1 - t2)/(k—1) = 2·287,7(300-15)/(1,4 –1) = 419·103 Дж=419 кДж.
Изменеие внутренней энергии в адиабатном процессе равно работе изменения объёма, поэтом U2 — U1 = - L1,2= - 419 кДж.
|
|
|
