 |
5.6. Вязкость жидкостей и газов
|
|
|
|
5. 6. Вязкость жидкостей и газов
Вязкость – способность жидкостей (газов) оказывать сопротивление сдвигу при сравнительно малых скоростях сдвига. Вязкость проявляется в виде сил внутреннего трения.
Остановимся на двух базовых законах трения – Ньютона (5. 16) и Бингама (5. 17).
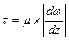, (5. 16)
, (5. 17)
где τ – касательное напряжение, Па;
μ – динамическая (абсолютная) вязкость, Па× с; в (5. 17) её часто называют пластической (структурной) вязкостью;
‑ производная от местной скорости жидкости (газа) ω по перпендикулярному вектору скорости направлению Z, с-1; часто называют градиентом скорости;
‑ начальное напряжение сдвига, Па.
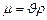, (5. 18)
где 
– кинематическая вязкость, 
.
Абсолютная и кинематическая вязкости жидкостей почти не зависят от давлений, если последние не превышают 20 МПа. Абсолютная вязкость газов также мало зависит от давления. Кинематическая вязкость газов из-за их сжимаемости от давления зависит. И абсолютная, и кинематическая вязкости жидкостей и газов существенно зависят от температуры. Чем температура выше, тем вязкости жидкостей меньше, у газов наоборот (таблицы 5. 4 и 5. 5).
Таблица 5. 4. Вязкость воды при Р = Ра
| Температура t, 0С | Абсолютная вязкость μ, Па× с | Кинематическая вязкость ,
|
| 1, 75× 10-3 1, 57× 10-3 1, 42× 10-3 10-3 | 1, 75× 10-6 1, 57× 10-6 1, 43× 10-6 10-6 |
Таблица 5. 5. Вязкость воздуха при Р = Ра.
| Температура t, 0С | Абсолютная вязкость μ, Па× с | Кинематическая вязкость ,
|
| -23 | 16× 10-6 17, 1× 10-6 18, 5× 10-6 19, 4× 10-6 23× 10-6 27× 10-6 30, 6× 10-6 | 1, 13× 10-5 1, 33× 10-5 1, 57× 10-5 1, 78× 10-5 2, 6× 10-5 3, 05× 10-5 5, 2× 10-5 |
Жидкости (газы), подчиняющиеся при сравнительно малых скоростях сдвига закону трения Ньютона называются ньютоновскими жидкостями (НЖ).
|
|
|
К НЖ (жидкостям в широком смысле слова) можно отнести воду, газы и их смеси, в том числе воздух, нефть, эмульсии, аэрозоли, масла в гидросистемах, некоторые пены и аэрированные жидкости, расплавленные металлы, спирты, ртуть и др.
Жидкости, подчиняющиеся при сравнительно малых скоростях сдвига закону трения Бингама называются бингамовскими жидкостями (БЖ). К БЖ можно отнести глинистые растворы (суспензии), некоторые пены и аэрированные жидкости, цементные растворы, масляные краски, грязи, некоторые пасты.
Закон трения Бингама является более общим по отношению к закону трения Ньютона (для НЖ 
). Для глинистых и цементных растворов в качестве начального напряжения сдвига выступаетдинамическое напряжение сдвига данного раствора.
5. 7. Основные уравнения гидростатики и газовой статики
Основное уравнение гидростатики:
, (5. 19)
где Р – абсолютное статическое давление, Па;
Р0 – внешнее статическое давление, Па;
h – глубина, м, измеряемая по вертикали.
Следствием основного уравнения гидростатики является закон Паскаля.
Закон Паскаля: внешнее давление передается во все точки жидкости без изменения.
Уравнению (5. 19) можно придать иной вид:
(5. 20)
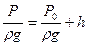, м, (5. 21)
где 
- абсолютный напор, м;
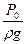- внешний напор, м.
В дифференциальной форме записи, справедливой как для жидкостей, так и для газов
, (5. 22)
где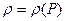 
- уравнение вида термодинамического процесса изменения состояния жидкости (газа).
|
|
|
Экспериментально доказано, что основные параметры состояния реального газа ( 
) приближенно связаны между собой в любом термодинамическом процессе в данный момент времени уравнением состояния совершенного (идеального) газа (уравнением Клапейрона – Менделеева) (5. 23) 
(5. 26).
Совершенным называется газ (смесь газов), подчиняющийся уравнению состояния.
Чем меньше плотность реального газа, тем меньше его поведение отличается от поведения совершенного газа.
, 
; (5. 23)
, Дж; (5. 24)
, 
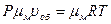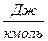; (5. 25)
, 
; (5. 26)
где R – удельная газовая постоянная, 
;
m – масса газа, кг;
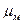- молярная масса газа, 
; для воздуха 
;
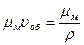- молярный объём газа, 
; при нормальных (физических) условиях
(Р=101325 Па, Т=273, 15 К) для любого совершенного газа 
22, 41410 .
- универсальная газовая постоянная, = 8314, 51 
.
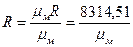. (5. 27)
1 кмоль (киломоль)– единица количества вещества, содержит количество частиц, равное числу Авогадро (6, 022× 1026 кмоль-1). Количество вещества равно 1 кмоль, если число килограмм вещества равно относительной молекулярной массе.
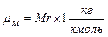, (5. 28)
где Mr – относительная молекулярная масса.
, (5. 29)
где nат – число атомов в молекуле химического элемента;
Аr – относительная атомная масса химического элемента;
y – количество химических элементов в соединении.
Строго говоря, единицей количества вещества в СИ является 1 моль, однако, пользоваться в расчетах величинами, в которые входит кмоль удобнее.
Связь между начальными и конечными значениями параметров состояния в изохорном (ρ = const, или 
= const), изобарном (Р = const) и изотермном (Т = const) термодинамических процессах определяет объединённый газовый закон:
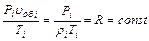(5. 30)
Процесс изменения состояния газа по глубине примем изотермным. Решая совместно (5. 22) и (5. 30) после интегрирования получим основное уравнение газовой статики:
, (5. 31)
|
|
|
где е ≈ 2, 72 – основание натуральных логарифмов.
Или 
(5. 32)
В уравнениях (5. 19), (5. 31) и (5. 32) при рассмотрении статики жидкости (газа) в буровой скважине следует учесть возможный наклон скважины:
h = L× cosθ, (5. 33)
где L – длина ствола скважины, м;
θ - среднее по длине скважины значение зенитного угла.
Разница между абсолютным и внешним давлениями жидкости называется весовым давлением Рв.
P – Po = Pв = ρ gh, (5. 34)
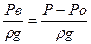, (5. 35)
где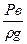 
- весовой напор жидкости, м.
При Ро = Ра (сосуд открыт, жидкость граничит с атмосферой) Рв = Ри.
Разница между абсолютным и атмосферным давлениями называется избыточным (манометрическим, сверхатмосферным) давлением Ри. Измеряется манометром.
Р – Ра = Ри, (5. 36)
, (5. 37)
где 
- избыточный (манометрический, сверхатмосферный) напор, м.
Разница между атмосферным и абсолютным давлениями называется вакуумметрическим давлением Рвак. Измеряется вакуумметром.
Ра – Р = Рвак, (5. 38)
, (6. 39)
где 
- вакуумметрический напор, м.
Определим максимальное значение высоты всасывания (вакуумметрического напора) воды насосом в атмосферных условиях. При всасывании в камере насоса Р> Рнп. Примем Р = Рнп (табл. 5. 2). При t = 40С Ра = 0, 981× 105 Па, ρ = 1000 
, Рнп ≈ 0. Тогда (5. 39) примет вид: 
|
|
|
