 |
5.9 Кинематика жидкости и газа
|
|
|
|
5. 9 Кинематика жидкости и газа
Изучает геометрию движения (без учёта сил).
Различают упорядоченное и неупорядоченное движение частиц жидкости (газа).
При неупорядоченном движении на основное движение всей массы частиц накладываются хаотические перемещения отдельных частиц друг относительно друга. При упорядоченном движении хаотические перемещения отсутствуют.
Нестационарным (неустановившемся) называют течение потока, при котором местная скорость частиц, проходящих через точку неподвижного пространства, является функцией координат и времени (истечение жидкости из сосуда при снижении её уровня).
При стационарном течении зависимость скорости частиц от времени отсутствует (поток, создаваемый шестерённым насосом).
Движение частицы жидкости (газа) при её бесконечно малом перемещении можно представить в виде суммы трёх движений:
- вращательного вокруг мгновенной оси;
- поступательного;
- деформационного, обусловленного изменением формы частицы.
Если вращательное движение частиц при их бесконечно малом перемещении отсутствует, а сами частицы движутся упорядоченно и поступательно, то течение называют потенциальным (безвихревым). Если при этом вся масса частиц движется по окружности, то её вращение называют потенциальным вращением ( 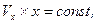 Vx – окружная скорость частицы, х – расстояние от оси вращения).
Vx – окружная скорость частицы, х – расстояние от оси вращения).
Если вращательное движение упорядоченно движущихся частиц при бесконечно малом перемещении имеется, то течение с бесконечно малыми визуально не наблюдаемыми вихрями называют вихревым, или микровихревым (непотенциальным). Течение с визуально наблюдаемыми вихрями называют вихревым, или макровихревым. Если вся масса частиц движется при этом по окружности, то вращение называют вихревым, или твердым, вращением (по закону вращения твердого тела 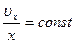 )
)
|
|
|
Если частицы движутся неупорядоченно, то течение называют турбулентным.
5. 10. Гидроаэродинамика потоков
Изучает движение жидкостей (газов) под действием сил.
1. Режимы течения жидкостей и газов.
При течении ньютоновских жидкостей (НЖ, τ 0 = 0) выделяют 2 основных режима.
Ламинарный (слоистый) режим течения. Слои в потоке не перемешиваются. Течение микровихревое (рис. 5. 1).

Рис. 5. 1. Ламинарный поток
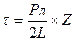 , (5. 51)
, (5. 51)
 , (5. 52)
, (5. 52)
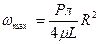 , (5. 53)
, (5. 53)
где τ – касательное напряжение, Па;
Рл – линейная потеря давления, Па;
L – длина потока, м;
ω – местная скорость, м/с.
Турбулентный (неупорядоченный) режим течения.
В ядре потока происходят хаотические перемещения частиц. Характерно интенсивное перемешивание (пульсации). Слои отсутствуют. В тонком пристенном условно ламинарном подслое движение частиц более упорядоченно, чем в ядре (рис. 5. 2).
С целью упрощения описания турбулентный поток осредняют, применяя осредненные во времени скорости и давления. Осредненный поток является моделью Рейнолдса-Буссинеска. Модель представляет собой особый ламинарный поток.
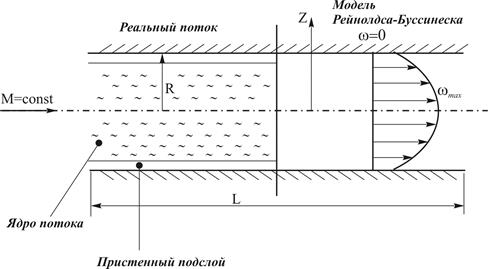
Рис. 5. 2. Турбулентный поток
При течении бингамовских жидкостей (БЖ, τ 0 > 0 ) также выделяют два основных режима.
Турбулентный режим течения (см. выше).
Структурный режим течения.
Течение в ядре потока – потенциальное, ядро движется как единое твердое тело. В пристенном слое, называемом градиентным слоем, течение ламинарное (рис. 5. 3)

Рис. 5. 3. Структурный поток
Для определения режима течения жидкости (газа) следует рассчитать величину числа Рейнолдса.
|
|
|
 , (5. 54)
, (5. 54)
где М – массовый расход жидкости (газа), кг/с;
dэ – эквивалентный диаметр потока, м;
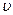 - средняя скорость течения потока, м/с;
- средняя скорость течения потока, м/с;
 - площадь поперечного сечения потока, м2;
- площадь поперечного сечения потока, м2;
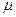 - абсолютная вязкость, Па× с;
- абсолютная вязкость, Па× с;
 - начальное напряжение сдвига, Па.
- начальное напряжение сдвига, Па.
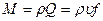 , (5. 55)
, (5. 55)
где  - объёмный расход, м3/с.
- объёмный расход, м3/с.
Под эквивалентным диаметром потока понимается диаметр такого воображаемого круглого потока, потеря давления в котором та же, что и в реальном потоке той же длины.
Для потоков круглого поперечного сечения
dэ = d, (5. 56)
для кольцевых концентричных ламинарных потоков
dэ ≈ 0, 82× (D-d), (5. 57)
где d – диаметр потока (для круглых в сечении потоков) или меньший диаметр потока (для кольцевых потоков), м;
D – больший диаметр потока, м.
Уравнение (5. 57) можно приближенно распространить как на структурные, так и на турбулентные кольцевые потоки.
Для ламинарного потока в плоской щели шириной h
 ,
,
для равносторонне – треугольного ламинарного потока со стороной а
 .
.
Для установления режима течения жидкости (газа) следует сравнить величину числа Рейнолдса (5. 54) с минимальным опытным значением критического числа Рейнолдса Rе кр. Данный прием позволяет установить режим лишь приближенно, т. к. не учитывает возможное закручивание потока за счет вращения труб, перемешивание жидкости из-за вибрации инструмента в скважине, эксцентричность кольцевого пространства и ряд других факторов.
Для НЖ (в т. ч. газов, τ 0 = 0):
Re кр = 2100 – для потоков круглого поперечного сечения; Re кр = 1600 – для кольцевых потоков.
Если Re ≥ Re кр, то режим течения турбулентный. Если Re < Re кр, то режим течения ламинарный.
Для БЖ (τ 0 > 0):
Re кр = 2000 – для круглых потоков; Re кр = 1000 – для кольцевых потоков.
Если Re ≥ Re кр, то режим течения турбулентный. Если Re < Re кр, то режим течения структурный.
2. Уравнение расхода для стационарного потока жидкости и газа.
Для жидкости и газа:
 , (5. 58)
, (5. 58)
|
|
|
Для жидкости (ρ = const):
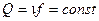 . (5. 59)
. (5. 59)
3. Уравнение импульса для стационарного потока жидкости и газа.
Приращение импульса за единицу времени равно сумме импульсов всех внешних сил за единицу времени (теорема Эйлера).
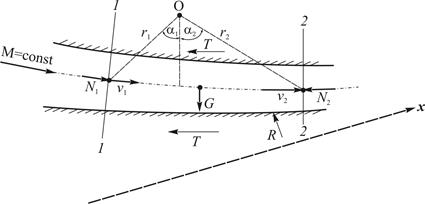
Рис. 5. 4. Схема внешних сил
Спроецировав все векторные величины (рис. 5. 4) на произвольную ось х, получим:
 , (5. 60)
, (5. 60)
где М – массовый расход, кг/с;
α / - коэффициент Буссинеска, учитывающий неравномерность распределения местных скоростей по сечению потока; для прямолинейного ламинарного движения в круглом трубопроводе α / = 4/3; для прямолинейного турбулентного течения в круглых трубах α /≈ 1, 03 – 1, 05.
 - проекции скоростей на ось х в сечениях 2-2 и 1-1 соответственно, м/с;
- проекции скоростей на ось х в сечениях 2-2 и 1-1 соответственно, м/с;
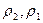 - плотности в соответствующих сечениях, кг/м3;
- плотности в соответствующих сечениях, кг/м3;
 - площади сечений, м2;
- площади сечений, м2;
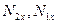 - проекции сил абсолютного давления в сечениях, Н;
- проекции сил абсолютного давления в сечениях, Н;
Тх – проекция силы внешнего трения, Н;
Rх – проекция силы давления стенок трубопровода на поток, Н;
Gx – проекция веса жидкости (газа) на ось х, Н.
4. Уравнение удара жидкости (газа).
Теорему Эйлера (5. 60) об изменении импульса можно применить в теории удара:
 , (5. 61)
, (5. 61)
где m – масса жидкости (газа), кг;
∆ t – время удара, с;
v1x, vox – проекции средних скоростей на произвольную ось х после удара и до удара соответственно, м/с;
Nуд х – проекция силы ударного давления, Н.
5. Уравнение момента импульса для стационарного потока жидкости и газа.
Приращение момента импульса потока жидкости (газа) относительно произвольной оси за единицу времени равно сумме моментов относительно той же оси всех внешних сил.
Рассмотрим все моменты (сил и скоростей) относительно оси ОУ, проходящей через точку О, перпендикулярной плоскости рисунка (рис. 5. 4) и направленной вверх.
Для нахождения момента нужно:
- спроецировать силу (скорость) на плоскость, перпендикулярную этой оси (ОУ) и найти величину проекции;
- из точки О провести перпендикуляр к линии действия проекции силы (скорости) и найти его длину;
|
|
|
- перемножить величину проекции силы (скорости) и длину перпендикуляра;
- определить знак момента относительно оси ОУ.
Момент силы (скорости) относительно оси имеет знак “+”, когда с положительного конца оси поворот, который стремится совершить сила (скорость) виден происходящим против хода часовой стрелки, а знак “-” – по ходу часовой стрелки.
 (5. 62)
(5. 62)
где r1, r2 – радиус-векторы центров масс сечений 2-2 и 1-1 соответственно (рис. 5. 4), м;
Ткр у – момент внешней силы относительно оси оу, Н× м (см. обозначения сил после формулы (5. 60)).
6. Уравнение энергии для стационарного потока жидкости и газа.
Уравнение энергии представляет собой форму записи закона сохранения энергии для потока.
 . (5. 63)
. (5. 63)
Уравнение (5. 63) называют дифференциальным уравнением энергии линейного стационарного потока, или дифференциальным уравнением движения потока, или обобщенным уравнением Бернулли, или уравнением первого закона термодинамики для проточной термодинамической системы в механической форме записи,
где ρ = ρ (P) – уравнение вида термодинамического процесса;
 - удельная потенциальная энергия давления;
- удельная потенциальная энергия давления;
gdz – удельная потенциальная энергия положения;
α – коэффициент Кориолиса, учитывающий неравномерность распределения местных скоростей по сечению потока; для прямолинейного ламинарного течения в круглых трубах α = 2, для прямолинейного круглого турбулентного потока α ≈ 1, 05 – 1, 15.
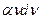 - удельная кинетическая энергия;
- удельная кинетическая энергия;
 - удельная работа сил внутреннего трения;
- удельная работа сил внутреннего трения;
 - удельная дополнительная механическая работа.
- удельная дополнительная механическая работа.
Если поток несжимаем (жидкость), то процесс изменения его состояния изохорный – ρ =const.
Газ в изохорном, изобарном и изотермном термодинамических процессов подчиняется уравнению (5. 30)
Уравнение политропного процесса для газа:
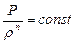 , (5. 64)
, (5. 64)
 , (5. 65)
, (5. 65)
 , (5. 66)
, (5. 66)
где n – показатель политропы;
Cn, Cp, Cv – удельные теплоемкости газа: политропная, изобарная и изохорная соответственно, Дж/(кг× К) (табл. 5. 6);
к – показатель адиабаты.
Таблица 5. 6. Теоретические значения удельных теплоемкостей газов
| Показатель Атомность молекулы газа | Удельные теплоемкости | Показатель адиабаты, к = Ср/Сv | |
| Изобарная Ср, Дж/(кг× К) | Изохорная Сv, Дж/(кг× К) | ||
| Одноатомная | 2, 5 R | 1, 5 R | 5/3 |
| Двухатомная | 3, 5 R | 2, 5 R | 1, 4 |
| Многоатомная | 4 R | 3 R | 4/3 |
Примечание: Воздух можно условно рассматривать в качестве газа, имеющего двухатомные молекулы.
|
|
|
Политропным (многообразным) называется термодинамический процесс, протекающий с неизменными теплоемкостями (параметры состояния Р, Т, ρ могут одновременно изменяться). Политропный процесс является моделью, позволяющей заменить реальный произвольный процесс на процесс с постоянными теплоемкостями, поддающийся расчету.
Адиабатным называется процесс, протекающий без теплообмена с внешней средой. Политропный процесс можно рассматривать как обобщающий по отношению к изобарному (n = 0), изотермному (n = 1), изохорному (n → ±∞ ) и адиабатному (n = к) процессам. Для жидкости (ρ = const) после умножения на ρ и интегрирования уравнение (5. 63) примет вид (рис. 5. 5):
 , (5. 67)
, (5. 67)
где P – абсолютное (или избыточное) давление, Па;
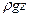 - геометрическое давление, Па; координата z центра масс сечения потока измеряется вдоль вертикали от произвольной горизонтальной плоскости (плоскости сравнения 0-0);
- геометрическое давление, Па; координата z центра масс сечения потока измеряется вдоль вертикали от произвольной горизонтальной плоскости (плоскости сравнения 0-0);
 - динамическое давление, Па;
- динамическое давление, Па;
 - давление торможения, Па;
- давление торможения, Па;
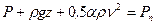 - полное давление, Па;
- полное давление, Па;
Ртр – потеря давления на внутреннее трение между сечениями потока 1-1 и 2-2, т. е. энергия, перешедшая в теплоту;
Рмех – дополнительное механическое давление (потеря давления на транспортирование шлама, на работу турбобура, гидроударника и т. д. ), Па.
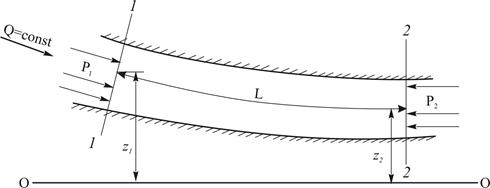
Рис. 5. 5. Течение потока между сечениями 1-1 и 2-2
Следует иметь ввиду, что в процессе течения как жидкости, так и газа всегда Рп1 > Рп2. Абсолютное (избыточное) давление по пути может увеличиваться, оставаться неизменным, либо уменьшаться. В горизонтальном трубопроводе постоянного сечения всегда Р1 > Р2.
Уравнение (5. 67) называют уравнением Бернулли для стационарного потока жидкости между сечениями 1-1 и 2-2.
 , (5. 68)
, (5. 68)
где Рл – линейная потеря давления (потеря по длине потока) на трение, Па;
Рм – местная потеря давления на трение, Па.
 . (5. 69)
. (5. 69)
В квадратичной области сопротивлений Р = f (v2), характерной для процеса промывки (продувки) скважины
 , (5. 70)
, (5. 70)
где λ – коэффициент линейных сопротивлений;
L – длина потока, м;
v – средняя скорость потока, м/с;
ξ – коэффициент местных сопротивлений.
Уравнение (5. 69) известно как формула Дарси-Вейсбаха, а (5. 70) – как формула Вейсбаха.
Линейные сопротивления вызваны наличием сил внутреннего трения в жидкости (газе) по длине трубопровода, местные – проявлением трения при изменении площади сечения трубопровода (сужением, расширением), при изгибе трубопровода и при соединении (разъединении) трубопроводов (тройники, крестовины, струйные аппараты).
Если режим течения НЖ (газа) турбулентный, то по эмпирической формуле А. Д. Альтшуля
 , (5. 71)
, (5. 71)
где Кэ – эквивалентная шероховатость поверхности магистрали, м.
Под эквивалентной подразумевается такая равнозернистая шероховатость, высота выступов которой Кэ вызывает сопротивление движению потока, соответствующее фактическому. Для трубопроводов из различных материалов значения Кэ приводятся в литературе. Для системы буровой снаряд – скважина в среднем Кэ = 0, 1× 10-3м.
Если БЖ движется турбулентно, то справедлива опытная формула Р. И. Шищенко.
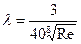 . (5. 72)
. (5. 72)
Если режим течения ламинарный или структурный, то справедливо аналитическое выражение:
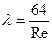 . (5. 73)
. (5. 73)
Анализ зависимостей (5. 69), (5. 71), (5. 73) и (5. 59) показывает, что:
- ламинарному и структурному режимам течения соответствует доквадратичная(линейная) область сопротивлений (  ):
):
 ,
, 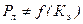 ;
;
- турбулентному режиму течения может соответствовать доквадратичная область сопротивлений в гидравлически гладких трубах:

 ;
;
доквадратичная область сопротивлений в гидравлически шероховатых трубах:
 ,
,
где 


квадратичная область сопротивлений в гидравлически шероховатых трубах:
 .
.

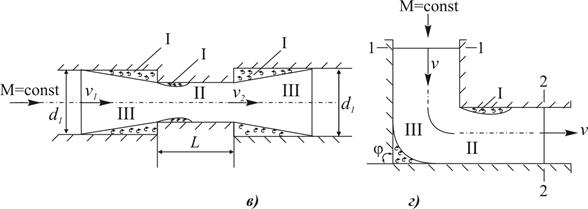
Рис. 5. 6. Местные сопротивления в квадратичной области
а) резкое расширение трубопровода; б) резкое сужение трубопровода; в) резкое сужение с последующим резким расширением трубопровода при условии сложения сопротивлений;
г) резкий изгиб трубопровода на произвольный угол φ.
I – зона вихревых вращений; II – область пониженного давления; III – транзитная струя.
Резкое расширение трубопровода (рис. 5. 6а). Решая совместно уравнение Бернулли (5. 67), уравнение расхода (5. 59) и уравнение импульса (5. 60) для стационарного изохорного потока между сечениями 1-1 и 2-2 получим:
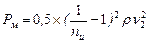 , (5. 73)
, (5. 73)
 , (5. 74)
, (5. 74)
где nи – степень изменения площади поперечного сечения трубопровода, nи< 1;
f1, f2 – площади соответствующих сечений, м2.
Резкое сужение трубопровода (рис. 5. 6б).
Опыты показывают, что потеря давления в сужающейся части транзитной струи мала в сравнении с потерей в расширяющейся части. Применяя (5. 73) для расширяющейся части получим:
 ; (5. 75)
; (5. 75)
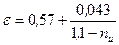 , (5. 76)
, (5. 76)
где ε – коэффициент сжатия транзитной струи.
Уравнение (5. 76) предложено А. Д. Альтшулем.
Опыты показывают, что потеря давления при резком сужении всегда меньше потери при расширении в трубопроводе с той же геометрией.
Резкое сужение с последующим резким расширением трубопровода (рис. 5. 6в).
Если резкое сужение расположено от резкого расширения на расстоянии L ≥ 50d1, то общее сопротивление можно найти путем сложения (5. 73) и (5. 75):
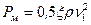 , (5. 77)
, (5. 77)
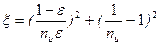 . (5. 78)
. (5. 78)
Резкий изгиб трубопровода на произвольный угол φ (рис. 5. 6г).
Пренебрегая потерями на сжатие транзитной струи получим формулу А. Д. Альтшуля:
 . (5. 79)
. (5. 79)
Величина дополнительного механического давления либо принимается по характеристике соответствующей гидравлической машины, либо, при учете затрат давления на транспортирование шлама, рассчитывается.
Если принять, что энергия потока жидкости расходуется на изменение потенциальной энергии положения выносимого шлама, получим:
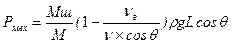 , (5. 80)
, (5. 80)
где Мш – массовый расход шлама, кг/с;
θ – среднее значение зенитного угла, градус.
 , (5. 81)
, (5. 81)
где vмех – механическая скорость бурения, м/с;
fз –площадь проекции забоя скважины на плоскость, нормальную оси скважины, м2.
Для колонкового бурения:
 , (5. 82)
, (5. 82)
для бескерного бурения:
 , (5. 83)
, (5. 83)
где Dс – диаметр скважины, м;
dk – диаметр керна, м.
Рассмотрим решение уравнения (5. 63) применительно к негоризонтальному изотермному (Т0 = const) газовому потоку длиной L на i-ом участке движения. Примем в соответствии с (5. 30), (5. 33), (5. 58), (5. 68), (5. 69) и (5. 80) dz = ±cosθ dL,
 ;
;
 .
.
Величиной α vdv можно пренебречь.
После интегрирования для первого участка движения (i = 1), имеющего длину Lх и выход в атмосферу (Р0, Т0), получим:
 , (5. 84)
, (5. 84)
 , (5. 85)
, (5. 85)
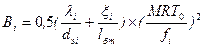 , (5. 86)
, (5. 86)
где Аi, Н/кг и Вi, (Н/с)2× м-3 – обозначения, введенные с целью упрощения записи формул, величины ими обозначенные самостоятельного физического смысла не имеют, Ai ≈ (8÷ 20), Bi ≈ (1010 ÷ 1018);
lбт – длина одной бурильной трубы (при условии движения воздушного потока внутри или снаружи бурильных труб), м.
Знак «+» - для восходящего потока газа. Знак «-» - для нисходящего потока газа.
Потенцирование формулы (5. 84) применительно к произвольному i-ому участку движения длиной Li приводит к выражению:
 , (5. 87)
, (5. 87)
где e ≈ 2, 71 – основание натуральных логарифмов;
Pi – абсолютное давление при входе газового потока на участок i, Па;
Pi-1 – абсолютное давление при входе газового потока на предыдущий (по ходу движения) участок, Па.
Решение уравнения (5. 63) применительно к горизонтальному (dz = 0) изотермному
(Т0 = const) газовому потоку приводит к уравнению следующего вида:
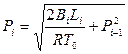 , (5. 88)
, (5. 88)
|
|
|


