 |
4.3. Уравнивание измеренных горизонтальных углов, вычисление дирекционных направлений
|
|
|
|
4. 3. Уравнивание измеренных горизонтальных углов, вычисление дирекционных направлений
В координатной ведомости (табл. 4. 2) подсчитывают сумму измеренных углов Σ β изм и теоретическую их сумму Σ β теор, которая определяется по формуле
∑ β теор = α +( н 180n − α к) − 360, (4. 7)
где n – количество углов теодолитного хода, включая примыкающие.
Вычисленные значения Σ β изм и Σ β теор записываются в координатной ведомости в графы 1, 2.
Затем определяют фактическую величину угловой невязки:
fβ = ∑ β изм − ∑ β теор (4. 8)
и допустимую величину угловой невязки:
fβ доп = 2' n. (4. 9)
Если fβ ≤ fβ доп, измерения на местности и последующие вычиcления являются верными.
Измеренные углы уравнивают (увязывают), то есть распределяют между ними фактическую угловую невязку fβ в виде поправок:
− fβ
ν =β . (4. 10)
n
Значения поправок округляют до 0, 1', берут со знаком, противоположным угловой невязке fβ , в итоге сумма поправок должна быть равна величине fβ .
Например, в табл. 4. 2 (графа 2) фактическая невязка fβ = +0, 5' разделена на 5 поправок (по количеству углов), которые соответственно равны –0, 1' каждая, а их сумма Σ vβ = –fβ = –0, 5'.
В графе 3 записываются уравненные горизонтальные углы, которые вычисляются по формуле
β i = β изм i + vβ i. (4. 11)
|
|
|
Сумма уравненных горизонтальных углов должна равняться теоретической сумме Σ β теор.
Дирекционные углы всех сторон хода последовательно вычисляются по формуле α і + 1 = α і + 180° – β і (α і + 1 < 360°). (4. 12) Дирекционный угол следующей по ходу стороны α i + 1 равен дирекционному углу предыдущей стороны α i плюс 180° минус уравненный правый по ходу угол β i между этими сторонами (при этом конечное значение угла α і + 1 не должно быть больше 360°). Например, в табл. 4. 2 определяем:
α М1-1 = 321°14' + 180° – 142°03, 4' = 359°10, 6';
α 1-2 = 359°10, 6' + 180° – 89°36, 4' = 449°34, 2' – 360° = 89°34, 2';
производим контроль:
α М2-Соть = α к = 168°51, 9' + 180° – 280°08, 9' = 68°43'.
Если все предыдущие вычисления верны, то в результате будет получено конечное значение α к (сторона хода М2-Соть).
Румб каждой стороны (графа 5) вычисляется со справочной целью в соответствии с формулами, которые должны быть известны студентам из предыдущих тем курса и учебников.
4. 4. Вычисление приращений координат и плановых координат пунктов хода
Приращения координат, которые называются вычисленными, определяют в соответствии с формулами:
| Δ Χ 'і = dі cosα і; | (4. 13) |
| Δ Υ 'і = dі sinα і. | (4. 14) |
При вычислениях на инженерном калькуляторе Δ Χ 'і и Δ Υ 'і величины α і необходимо определять в градусах.
Например, для стороны М1-1 дан α = 359°10, 6', определяем α 0 = = 10, 6' / 60' + 359° = 359, 177°, вносим в память калькулятора х → М и при d = 2011, 7 м получаем Δ Χ 'і = +2011, 49 м; Δ Υ 'і = –28, 91 м. Величины Δ Χ 'і и Δ Υ 'і записывают в ведомость (см. табл. 4. 2, графы 7 и 8) с округлением до 0, 01 м и со знаком плюс или минус.
Определяют суммы вычисленных приращений координат Σ Δ Χ ' и Σ Δ Υ ' (см. пример табл. 4. 2).
Вычисляют теоретические значения сумм приращений координат:
|
|
|
| ∑ Δ Χ теор = Χ к – Χ н; | (4. 15) |
| ∑ Δ Υ теор = Υ к – Υ н. | (4. 16) |
Невязки вычисленных приращений координат определяют в соответствии с формулами:
| fΧ = ∑ Δ Χ ' – ∑ Δ Χ теор; | (4. 17) |
| fΥ = ∑ Δ Υ ' – ∑ Δ Υ теор. Например, в табл. 4. 2 fΧ = +0, 28 м; fΥ = –1, 86 м. Абсолютная невязка хода | (4. 18) |
fs =
| X |
| Y |
| f |
| f |
| + |
а ее допустимая величина будет равна
∑ d
fs доп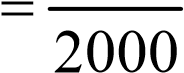 
(4. 20)
(одна двухтысячная от длины хода).
Абсолютная невязка хода fs не должна превышать величину ее допустимого значения fs доп.
Если абсолютная невязка хода удовлетворяет условиям допустимости, то уравнивают вычисленные приращения координат Δ Χ і и Δ Υ і. С этой целью фактические невязки fX и fY преобразуют в поправки ν Xi и ν Yi к соответствующим величинам Δ Χ і и Δ Υ і.
Вначале вычисляются коэффициенты:
− fX
KX = ; (4. 21)
∑ d
− fY
KY = . (4. 22)
∑ d
Затем определяются поправки пропорционально длине соответствующих сторон хода:
| ν Xi = KX di; | (4. 23) |
| ν Y = KY di. | (4. 24) |
i
Знак поправок ν Xi и ν Yi противоположен знаку соответствующей невязки fX или fY, а сумма поправок должна быть равна величине соответствующей невязки:
| ∑ ν Xi = –f X; | (4. 25) |
| ∑ ν Y = – fY. | (4. 26) |
i
Например, на основании данных табл. 4. 2 определяем коэффициенты:
KX =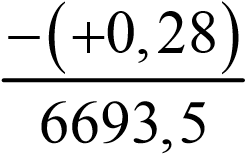 
=− 0, 000041;
KY =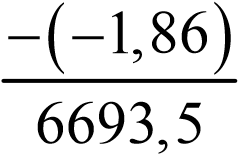 
=+0, 000278.
Поправки вычислены в табл. 4. 4.
Таблица 4. 4 Вычисление поправок к приращениям координат
| Горизонтальное проложение, м | Поправки, м | ||
| ν Xi | ν Yi | ||
| d1 = 2011, 7 d2 = 2535, 0 d3 = 1255, 3 d4 = 891, 5 | –0, 08 –0, 11 –0, 05 –0, 04 | +0, 56 +0, 70 +0, 35 +0, 25 | |
|
|
|
Вычисленные значения поправок записывают в графах 7 и 8 координатной ведомости над соответствующими значениями Δ Χ 'і и Δ Υ 'і. Затем вычисляют уравненные приращения координат в соответствии с формулами:
| Δ Χ і = Δ Χ 'і + ν Xi; | (4. 27) |
| Δ Υ і = Δ Υ 'і + ν Y , | (4. 28) |
i
и их значения записывают в графах 9 и 10 координатной ведомости
(табл. 4. 2).
Вычисляют суммы уравненных приращений координат, записывают полученные значения в графах 9 и 10 и выполняют контроль вычислений:
| ∑ Δ Χ = ∑ Δ Χ теор; | (4. 29) |
| ∑ Δ Υ = ∑ Δ Υ теор. | (4. 30) |
Координаты вершин теодолитного хода (графа 11 и 12 координатной ведомости) начинают последовательно вычислять от известных координат Χ н, Υ н начальной точки хода (М1) и заканчивают для контроля определением известных координат Χ к, Υ к конечной точки (М2). При этом координата каждой следующей точки хода равна сумме координаты предыдущей точки и уравненного приращения:
Χ і + 1 = Χ і + Δ Χ і; (4. 31)
Υ і + 1 = Υ і + Δ Υ і. (4. 32)
Например, в табл. 4. 2 определяем:
абсциссы точек:
Χ 1 = Χ н + Δ Χ М1-1 = 1600, 12 + 2011, 41 = 3611, 53 м;
Χ 2 = Χ 1 + Δ Χ 1-2 = 3611, 53 + 18, 91 = 3630, 44 м;
Χ 3 = Χ 2 + Δ Χ 2-3 = 3630, 44 + (–1234, 18) = 2396, 26 м;
Χ к = Χ 3 + Δ Χ 3-М2 = 2396, 26 + (–874, 76) = 1521, 50 м; ординаты точек:
Υ 1 = Υ н + Δ Υ М1-1 = 2322, 00 + (–28, 35) = 2293, 65 м;
Υ 2 = Υ 1 + Δ Υ 1-2 = 2293, 65 + 2535, 63 = 4829, 28 м;
Υ 3 = Υ 2 + Δ Υ 2-3 = 4829, 28 + (–229, 24) = 4600, 04 м; Υ к = Υ 3 + Δ Υ 3-М2 = 4600, 04 + 172, 42 = 4772, 46 м.
|
|
|
