 |
4.5. Вычисление дирекционного угла и длины линии М2-М1
|
|
|
|
4. 5. Вычисление дирекционного угла и длины линии М2-М1
Сторона М2-М1 лесоучастка не определена при проведении теодолитной съемки местности, но ее длина и дирекционный угол необходимы при оформлении планшета.
В соответствии с обратной геодезической задачей находим румб rМ2-М1:
| tgrM2-M1 = М1 M2 = , XМ1 − XM2 Δ X | (4. 33) |
| ⎛ Δ Y ⎞ rМ2-М1 = arctg⎜ ⎟. ⎝ Δ X ⎠ | (4. 34) |
Y − Y Δ Y
По знакам разностей (приращений) координат Δ Y и Δ X определяются четверть и наименование румба линии М2-М1.
Дирекционный угол вычисляется в соответствии с формулами взаимосвязи между α и r, которые должны быть известны студентам из предыдущих тем курса и учебников. Длина линии М2-М1 рассчитывается с контролем по двум из трех формул:
| dМ2-М1 =; cosα | (4. 35) |
| Δ Y dМ2-М1 = ; sinα | (4. 36) |
Δ X
dМ2-М1 = Δ +Δ X 2 Y 2. (4. 37)
В нашем случае в соответствии с табл. 4. 2 находим:
Δ XМ2-М1 = 1600, 12 – 1521, 50 = +78, 62 м;
Δ YМ2-М1 = 2322, 00 – 4772, 46 = –2450, 46 м;
tgr =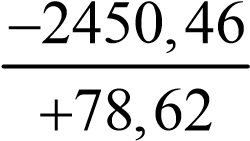 
=− 31, 181; °
arctgr = 88, 16°.
В соответствии со знаками приращений координат Δ Y (–) и Δ X (+) определяем четверть – СЗ и наименование румба линии М2-М1 – СЗ: 88°10'.
Дирекционный угол линии М2-М1 равен 271°50'.
Длина линии М2-М1равна
dМ2-М1 = 78, 622 + − ( 2450, 46)2 = 2451, 7 м.
Лабораторная работа № 5 СОСТАВЛЕНИЕ ПЛАНА ТЕОДОЛИТНОГО ХОДА.
Для составления учебного лесоустроительного планшета необходимо иметь:
|
|
|
1) лист чертежной бумаги формата А2;
2) металлическую линейку;
3) треугольник; остро заточенный простой карандаш М-2М или механический «0, 5 мм»;
4) циркуль и циркуль-измеритель; 5) лекала для рисования кривых.
План вначале составляется карандашом, тонкими линиями, оформляется подписями и условными знаками согласно требованиям лесоустроительных планшетов, после самопроверки и проверки преподавателем вычерчивается соответствующими цветами.
5. 1. Нанесение на план координатной сетки и пунктов по их координатам
На листе чертежной бумаги формата А2 строят сетку квадратов 10× 10 см общим размером 30× 40 см. Применяя линейку Дробышева, используют свойства прямоугольного треугольника с отношением сторон 3: 4: 5.
Построение сетки квадратов линейкой Дробышева состоит в следующем:
| вают в положение АС перпендикулярно линии АВ на глаз. Совместив нулевой штрих с точкой А, проводят штрихи через три последу- | А В Рис. 5. 1. Принцип построения координатной сетки линейкой Дробышева |
1)
| С |
| D |
2) линейку приклады-
ющих выреза линейки. Линейку перекладывают в положение ВС – по диагонали и, совместив нулевой штрих линейки с точкой В, по пятому скошенному вырезу прочерчивают штрих. Полученная в пересечении точка С является вершиной перпендикуляра к линии АВ с основанием в точке А;
3) подобное построение повторяют в точке В, в результате получают точку D, которая является вершиной перпендикуляра с основанием в точке В;
4) приложив линейку к точкам С и D, нужно проверить расстояние между ними. Оно должно быть равно 40 см. Контролем служит совпадение трех штрихов, а также при контроле правильности построения сетки квадратов проверяют длины всех сторон квадратов и их диагоналей. Если расхождение против точных сторон квадратов превышает 0, 2 мм, сетку квадратов перечерчивают.
|
|
|
Точность построения сетки дополнительно проверяют измерением длины обоих диагоналей каждого квадрата (отклонение от теоретического значения 141, 4 мм должно составлять не более чем ±0, 4 мм).
Масштаб составляемого планшета равен 1: 10 000 (в 1 см 100 м). Стороны квадратов координатной сетки 10× 10 см в масштабе плана равны 1000 м. Чтобы разместить контур лесного участка в границах координатной сетки, определяют наименьшее и наибольшее значения координат пунктов теодолитного хода по оси X.
Линии координатной сетки подписывают в целых тысячах метров так, чтобы точки с наибольшей и наименьшей абсциссами X разместились примерно на одинаковых расстояниях от противоположных сторон координатной рамки. Аналогичные действия выполняют относительно оси Y с учетом, что за границами лесного участка на востоке необходимо расположить реку Соть. Пример оцифровки координатной сетки и оформления рамок планшета показан на рис. 5. 2.
Для нанесения на план пункта М1 по его координатам (Χ н = = 1600, 12 м; Υ н = 2322, 00 м) вначале находят квадрат сетки, в который попадает пункт М1 (рис. 5. 2). Вычисляют расстояния Δ X = XМ1 – Xю = = 1600, 12 – 1000 = 600, 12 м и Δ Y = YМ1 – Yз = 2322, 00 – 2000 = = 322, 00 м от южной и западной сторон квадрата сетки. В масштабе плана указанные расстояния равны Δ X = 60, 0 мм, Δ Y = 32, 2 мм. Расстояние Δ X отмечается на двух сторонах квадрата (см. рис. 5. 2). При нанесении точки Ml отрезок Δ Y отмечается на линии, проходящей через метки Δ X.
Нанесение производится при помощи масштабной линейки и циркуля-измерителя с погрешностью не грубее 0, 1–0, 2 мм. Обозначают пункт М1 легким уколом карандаша (диаметр поставленной точки не должен превышать 0, 2 мм).
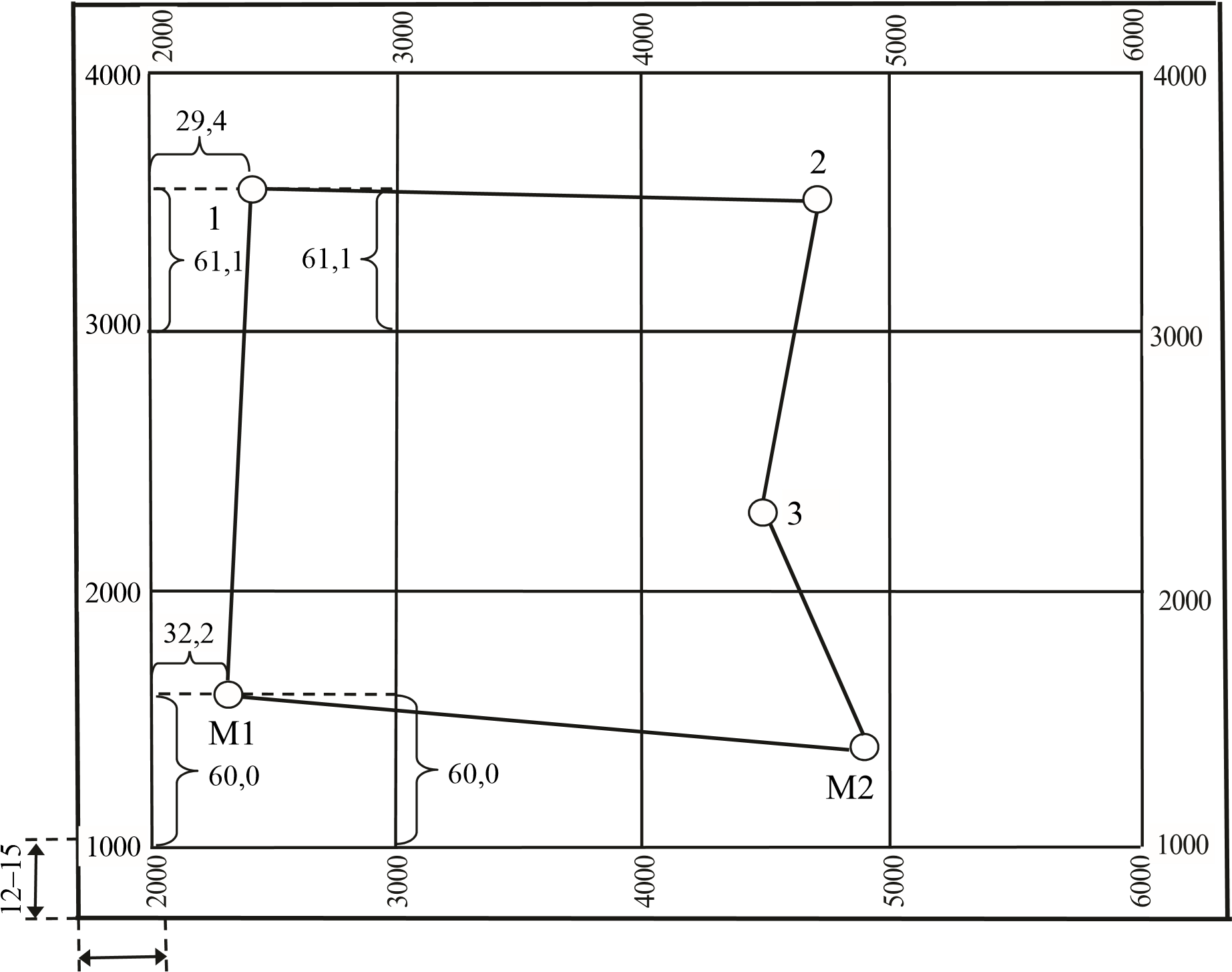
12–15
1: М = 1: 10 000
В 1 см 100 м
Рис. 5. 2. Координатная сетка и нанесение точек по их координатам
Аналогичным образом наносят на план точки 1, 2, 3 и М2.
|
|
|
Правильность положения точек на плане проверяется измерением расстояний между ними, известных из координатной ведомости (графа 6) и учитываемых в масштабе плана. Например, расстояние dМ1-1 = 2011, 7 м на плане должно быть равно 201, 2 мм, допускается отклонение до ±0, 5 мм. (Длина отрезка М2-М1 была определена решением обратной геодезической задачи – пункт 4. 5. )
В случае недопустимых расхождений нужно продублировать нанесение пунктов или проверить точность построения сетки – в первую очередь проверяют те квадраты, где размещались вершины хода.
|
|
|
