 |
Задача 1.1. Матрица парных коэффициентов корреляции
|
|
|
|
Кировский филиал
| Кафедра |
«_____________________________________________________________»
Контрольная работа №
по _____________________ на тему №24:
_________________________________________________________________
| Студентка | Вохмянина Юлия Алексеевна |
| Специальность | Бакалавр экономики |
| Образование № личного дела | Первое высшее 10ФЛБ00800 |
| Курс | |
| Преподаватель | |
Киров 2012г. (2013г.)
Содержание
ИСХОДНЫЕ ДАННЫЕ.. 3
Задача 1. Эконометрическое моделирование стоимости квартир в Московской области. 3
Задача 2. Исследовать динамику экономического показателя на основе анализа одномерного временного ряда. 5
РЕШЕНИЕ.. 6
Задача 1.1. Матрица парных коэффициентов корреляции. 6
Задача 1.2. Поле корреляции результативного признака. 8
Задача 1.3. Параметры линейной парной регрессии. 8
Задача 1.4. Оценка качества моделей. 11
Задача 1.5. Прогнозирование среднего значения. 17
Задача 1.6. Пошаговая множественная регрессия. 19
Задача 1.7. Оценка качества многофакторной модели. 22
Задача 2.1. Проверка наличия аномальных наблюдений. 26
Задача 2.2. Построение линейной модели. 27
Задача 2.3. Оценка адекватности модели. 28
Задача 2.4. Оценка точности модели. 30
Задача 2.5. Осуществление прогноза. 31
Задача 2.6. Графическое представление результатов моделирования и прогнозирования. 33
СПИСОК ЛИТЕРАТУРЫ... 34
Исходные данные
Задача 1. Эконометрическое моделирование стоимости квартир в Московской области
Задача 1. Эконометрическое моделирование стоимости квартир в Московской области.
Исследуемые факторы: Y, X1, X2, X4. Номера наблюдений: 41-80.
Наименования показателей
| Обозначение | Наименование показателя | Единица измерения (возможные значения) |
| Y | цена квартиры | тыс. долл. |
| X1 | город области | Подольск/Люберцы |
| X2 | число комнат в квартире | |
| X4 | жилая площадь квартиры | кв. м |
Исходные данные для эконометрического моделирования стоимости квартир
|
|
|
| № | Y | X1 | X2 | X4 |
| 62,2 | ||||
| 61,1 | 34,8 | |||
| 18,7 | ||||
| 27,7 | ||||
| 92,5 | ||||
| 130,5 | ||||
| 59,2 | ||||
| 49,5 | ||||
| 18,9 | ||||
| 86,9 | 58,7 | |||
| 18,5 | ||||
| 70,3 | 34,8 | |||
1. Рассчитайте матрицу парных коэффициентов корреляции; оцените статистическую значимость коэффициентов корреляции.
2. Постройте поле корреляции результативного признака и наиболее тесно связанного с ним фактора.
3. Рассчитайте параметры линейной парной регрессии для каждого фактора Х.
4. Оцените качество каждой модели через коэффициент детерминации, среднюю ошибку аппроксимации и F-критерий Фишера. Выберите лучшую модель.
5. Для выбранной модели осуществите прогнозирование среднего значения показателя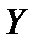 
при уровне значимости 
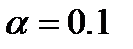, если прогнозное значения фактора 
составит 80% от его максимального значения. Представьте графически: фактические и модельные значения, точки прогноза.
6. Используя пошаговую множественную регрессию (метод исключения или метод включения), постройте модель формирования цены квартиры за счёт значимых факторов. Дайте экономическую интерпретацию коэффициентов модели регрессии.
|
|
|
7. Оцените качество построенной модели. Улучшилось ли качество модели по сравнению с однофакторной моделью? Дайте оценку влияния значимых факторов на результат с помощью коэффициентов эластичности, b- и D- коэффициентов.
Задача 2. Исследовать динамику экономического показателя на основе анализа одномерного временного ряда
Задача 2. Исследовать динамику экономического показателя на основе анализа одномерного временного ряда.
В течение девяти последовательных недель фиксировался спрос Y(t) (млн. р.) на кредитные ресурсы финансовой компании. Временной ряд Y(t) этого показателя приведен ниже в таблице.
| Номер варианта | Номер наблюдения (t = 1, 2, …, 9) | ||||||||
Задание.
1. Проверить наличие аномальных наблюдений.
2. Построить линейную модель 
, параметры которой оценить МНК (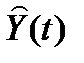
– расчетные, смоделированные значения временного ряда).
3. Оценить адекватность построенных моделей, используя свойства независимости остаточной компоненты, случайности и соответствия нормальному закону распределения (при использовании R/S-критерия взять табулированные границы 2,7-3,7).
4. Оценить точность моделей на основе использования средней относительной ошибки аппроксимации.
5. Осуществить прогноз спроса на следующие две недели (доверительный интервал прогноза рассчитать при доверительной вероятности р = 70%).
6. Фактические значения показателя, результаты моделирования и прогнозирования представить графически.
Решение
Задача 1.1. Матрица парных коэффициентов корреляции
1. Рассчитайте матрицу парных коэффициентов корреляции; оцените статистическую значимость коэффициентов корреляции.
Парные коэффициенты корреляции рассчитываются по формуле:
,
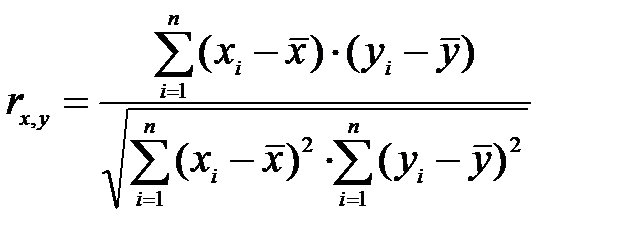где n – объем выборки, 
- значение факторного признака, 
- значение результативного признака, 
- среднее значение факторного признака, 
- среднее значение результативного признака.
Используя инструмент «Корреляция» пакета «Анализ данных» в Excel получим матрицу парных коэффициентов корреляции.
|
|
|
| Y | X1 | X2 | X4 | |
| Y | ||||
| X1 | -0,01126 | |||
| X2 | 0,751061 | -0,0341 | ||
| X4 | 0,874012 | -0,0798 | 0,868524 |
Качественно оценим взаимосвязь между результирующим признаком Y и каждым из факторов Хj, j=1,2,4 (силу зависимости определим по шкале Чеддока):
· 
, значит, между переменными Y и Х1 наблюдается обратная корреляционная зависимость. Однако зависимость между этими показателями очень слабая.
· 
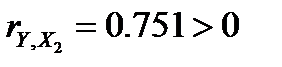, значит, между переменными Y и Х2 наблюдается прямая корреляционная зависимость: чем больше число комнат в квартире, тем выше ее цена.
· 
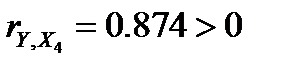, значит, между переменными Y и X4 наблюдается прямая корреляционная зависимость: чем больше жилая площадь квартиры, тем выше ее цена.
– эта зависимость высокая, ближе к весьма высокой.
Это означает, что на 87,4 зависимая переменная Y (цена квартиры) зависит от показателя Х4 жилая площадь квартиры.
Оценим теперь статистическую значимость каждого коэффициента. Для этого рассчитаем значения t-критерия Стьюдента для каждого коэффициента.
,
где 
- парный коэффициент корреляции результативного признака Y и факторного Xj, j=1,2,4, n – объем выборки.
ty,x1 = 0,069 ty,x2 = 7,012 ty,x4 = 11,088 tкр. = (0,05; 38) = 2,024
По таблице критических точек распределения Стьюдента (или с помощью функции СТЬЮДРАСПОБР в Excel) при уровне значимости α=5% и числе степеней свободы k=n–2=40–2=38 определим критическое значение: tкр = 2.024
Т.к.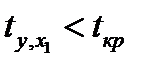 
(0,069<2.024), то коэффициент 
не является значимым. На основании выборочных данных нет оснований утверждать, что зависимость между ценой квартиры Y и городом области Х1 существует.
Т.к. 
(7,012>2.024), то коэффициент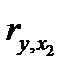 
является значимым. На основании выборочных данных есть основания утверждать, что зависимость между ценой квартиры Y и числом комнат в квартире Х2 существует.
Т.к. 
(11,088>2.024), то коэффициент 
является значимым (значимо отличается от нуля). На уровне значимости 5% выборочные данные позволяют сделать вывод о наличии тесной линейной корреляционной зависимости между признаками Y и Х4. Зависимость между ценой квартиры Y и жилой площадью квартиры Х4 является достоверной.
|
|
|
Таким образом, наиболее тесная и значимая зависимость наблюдается между ценой квартиры Y и жилой площадью квартиры Х4.
|
|
|
