Задача 1.4. Оценка качества моделей

4. Оцените качество каждой модели через коэффициент детерминации, среднюю ошибку аппроксимации и F – критерий Фишера. Выберите лучшую модель.

Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции , называемый коэффициентом детерминации. Коэффициентом детерминации характеризует долю вариации результативного признака Y, учтенную в модели, и обусловленную влиянием фактора X.

4.1. Коэффициент детерминации определяется по формуле:

где - сумма квадратов отклонений, объясненная регрессией, и общая сумма квадратов отклонений соответственно.

Коэффициенты детерминации R-квадрат определены для каждой модели инструментом «Регрессия» пакета «Анализ данных» в Excel (таблица «Регрессионная статистика»):

Модель (1): 0,0001

Модель (2): 0,564

Модель (3): 0,764

Таким образом, вариация цены квартиры Y на 76,4% объясняется по уравнению (3) изменением жилой площади квартиры Х₄; на 56,4% по уравнению (2) изменением общей площади квартиры Х₂; на 0,01% по уравнению (1) вариацией города области Х₁, т.е. наиболее адекватной моделью уравнения регрессии является зависимость цены квартиры от жилой площади квартиры Y = f (Х ₄).

4.2. Для вычисления средней относительной ошибки аппроксимации рассмотрим остатки модели , содержащиеся в столбце «Остатки» таблицы «Вывод остатка». Дополним таблицу столбцом относительных погрешностей, которые вычислим по формуле с помощью функции ABS в Excel.

Выполнение расчетов для модели (1):

Наблюдение	Y	Предсказанное Y	Остатки	Отн. погрешность
		100,5333333	-62,53333333	164,5614035
	62,2	100,5333333	-38,33333333	61,62915327
		101,8136364	23,18636364	18,54909091
	61,1	100,5333333	-39,43333333	64,53900709
		101,8136364	-34,81363636	51,96065129
		101,8136364	-8,813636364	9,477028348
		100,5333333	17,46666667	14,80225989
		101,8136364	30,18636364	22,8684573
	92,5	101,8136364	-9,313636364	10,06879607
		100,5333333	4,466666667	4,253968254
		100,5333333	-58,53333333	139,3650794
		100,5333333	24,46666667	19,57333333
		101,8136364	68,18636364	40,10962567
		101,8136364	-63,81363636	167,930622
	130,5	101,8136364	28,68636364	21,98188784
		101,8136364	-16,81363636	19,78074866
		101,8136364	-3,813636364	3,891465677
		101,8136364	26,18636364	20,45809659
		101,8136364	-16,81363636	19,78074866
		100,5333333	59,46666667	37,16666667
		101,8136364	-41,81363636	69,68939394
		100,5333333	-59,53333333	145,203252
		100,5333333	-10,53333333	11,7037037
		101,8136364	-18,81363636	22,66703176
		101,8136364	-56,81363636	126,2525253
		101,8136364	-62,81363636	161,0606061
	86,9	101,8136364	-14,91363636	17,16183701
		101,8136364	-61,81363636	154,5340909
		101,8136364	-21,81363636	27,26704545
		101,8136364	125,1863636	55,14817781
		101,8136364	133,1863636	56,67504836
		100,5333333	-60,53333333	151,3333333
		100,5333333	-33,53333333	50,04975124
		100,5333333	22,46666667	18,26558266
		101,8136364	-1,813636364	1,813636364
		100,5333333	4,466666667	4,253968254
	70,3	100,5333333	-30,23333333	43,00616406
		100,5333333	-18,53333333	22,60162602
		100,5333333	179,4666667	64,0952381
		100,5333333	99,46666667	49,73333333
Среднее	101,2375	101,2375		54,1315859

 

 

 

По столбцу относительных погрешностей найдем среднее значение (с помощью функции СРЗНАЧ Excel).

Выполнение расчетов для модели (2):

Наблюдение	Y	Предсказанное Y	Остатки	Отн. погрешность
		43,57706835	-5,577068345	14,67649565
	62,2	79,61483813	-17,41483813	27,99813204
		115,6526079	9,347392086	7,477913669
	61,1	79,61483813	-18,51483813	30,3025174
		43,57706835	23,42293165	34,95959948
		79,61483813	13,38516187	14,39264717
		115,6526079	2,347392086	1,989315327
		115,6526079	16,34739209	12,38438794
	92,5	115,6526079	-23,15260791	25,02984639
		151,6903777	-46,6903777	44,46702638
		43,57706835	-1,577068345	3,754924632
		115,6526079	9,347392086	7,477913669
		151,6903777	18,3096223	10,77036606
		43,57706835	-5,577068345	14,67649565
	130,5	151,6903777	-21,1903777	16,23783732
		79,61483813	5,385161871	6,335484554
		151,6903777	-53,6903777	54,78609969
		151,6903777	-23,6903777	18,50810758
		115,6526079	-30,65260791	36,06189166
		115,6526079	44,34739209	27,71712005
		43,57706835	16,42293165	27,37155276
		43,57706835	-2,577068345	6,28553255
		151,6903777	-61,6903777	68,54486411
		151,6903777	-68,6903777	82,7594912
		43,57706835	1,422931655	3,162070344
		43,57706835	-4,577068345	11,73607268
	86,9	115,6526079	-28,75260791	33,08700565
		43,57706835	-3,577068345	8,942670863
		79,61483813	0,385161871	0,481452338
		151,6903777	75,3096223	33,17604507
		151,6903777	83,3096223	35,45090311
		43,57706835	-3,577068345	8,942670863
		43,57706835	23,42293165	34,95959948
		151,6903777	-28,6903777	23,32551032
		115,6526079	-15,65260791	15,65260791
		115,6526079	-10,65260791	10,14534087
	70,3	79,61483813	-9,314838129	13,25012536
		115,6526079	-33,65260791	41,03976575
		151,6903777	128,3096223	45,82486511
		151,6903777	48,3096223	24,15481115
Среднее	101,2375	101,2375		23,457427

 

 

 

 

По столбцу относительных погрешностей найдем среднее значение (с помощью функции СРЗНАЧ Excel).

Выполнение расчетов для модели (3):

Наблюдение	Y	Предсказанное Y	Остатки	Отн. погрешность
		44,17866562	-6,178665622	16,25964637
	62,2	86,27023362	-24,07023362	38,69812478
		98,65010656	26,34989344	21,07991476
	61,1	83,29906411	-22,19906411	36,33234715
		43,43587325	23,56412675	35,17033844
		65,71964454	27,28035546	29,33371555
		143,2176491	-25,21764914	21,3708891
		106,0780303	25,92196968	19,63785582
	92,5	135,7897254	-43,28972537	46,79970311
		113,5059541	-8,505954083	8,10090865
		41,70269103	0,297308966	0,70787849
		106,0780303	18,92196968	15,13757574
		135,7897254	34,21027463	20,12369096
		36,75074186	1,249258142	3,287521425
	130,5	160,5494713	-30,04947125	23,02641475
		81,31828444	3,68171556	4,33143007
		103,6020557	-5,602055731	5,716383399
		143,7128441	-15,71284406	12,27565942
		120,9338778	-35,93387785	42,27515041
		101,1260811	58,87391886	36,79619929
		46,65464021	13,34535979	22,24226632
		31,79879268	9,201207317	22,44196907
		113,5059541	-23,50595408	26,11772676
		119,6958906	-36,69589055	44,21191633
		43,93106816	1,068931837	2,375404081
		41,70269103	-2,702691034	6,929977011
	86,9	142,4748568	-55,57485676	63,9526545
		51,60658939	-11,60658939	29,01647346
		96,17413197	-16,17413197	20,21766496
		222,448836	4,55116405	2,004918084
		219,9728614	15,02713864	6,39452708
		34,27476727	5,725232729	14,31308182
		42,94067833	24,05932167	35,90943533
		133,3137508	-10,31375079	8,385163241
		88,7462082	11,2537918	11,2537918
		115,9819287	-10,98192867	10,45897969
	70,3	83,29906411	-12,99906411	18,49084511
		115,9819287	-33,98192867	41,44137643
		207,5929884	72,40701158	25,85964699
		145,6936237	54,30637627	27,15318814
Среднее	101,2375	101,2375		21,89080885

 

 

 

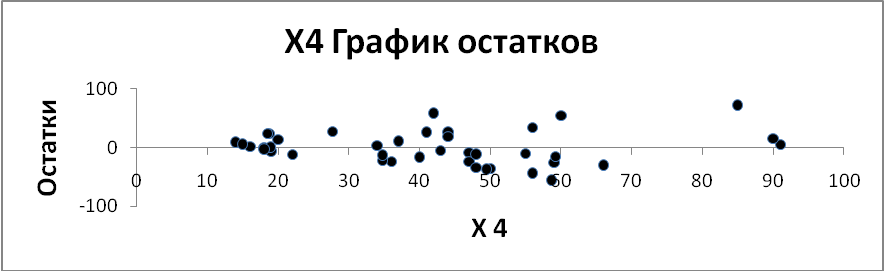
По столбцу относительных погрешностей найдем среднее значение (с помощью функции СРЗНАЧ Excel).

, это свидетельствует о том, что качество модели не удовлетворительное. Ближе всех к 7% значение .

Ни одну из моделей по данному критерию оценки считать приемлемой нельзя. Лучшей моделью является зависимость цены квартиры от жилой площади квартиры Y = f (Х ₄).

 

4.3. Проверим значимость полученных уравнений с помощью
F – критерия Фишера.

,

k – количество факторов, включенных в модель.

F – статистики определены инструментом «Регрессия» пакета «Анализ данных» в Excel (таблицы «Дисперсионный анализ»):

F ₁ = 0,0048179 F ₂ = 49,17440478 F ₃ = 122,9467831

С помощью функции РАСПОБР Excel или по таблице найдем значение F_кр=4.098 для уровня значимости α=5%, и чисел степеней свободы k₁=1, k₂=38.

F₂>F_кр, F₃>F_кр следовательно, уравнения модели (2) и (3) являются значимыми, их использование целесообразно, зависимая переменная Y достаточно хорошо описывается включенными в модели (2) и (3) факторными переменными Х₂ и Х_4.

F₁<F_кр, следовательно уравнение модели (1) не является значимым и использование этой модели нецелесообразно.

Вывод: на основании оценки качества моделей по коэффициенту детерминации, средней ошибке аппроксимации и критерию Фишера наилучшей является модель (3) зависимости цены квартиры от ее жилой площади: .

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: