Задача 1.3. Параметры линейной парной регрессии

3. Рассчитайте параметры линейной парной регрессии для каждого фактора Х.

Для построения линейной парной модели , j=4,5,6 используем инструмент «Регрессия» пакета «Анализ данных» в Excel.

Входной фактор Х1:

Результаты вычислений представлены в таблицах:

Регрессионная статистика
Множественный R	0,011259267
R-квадрат	0,000126771
Нормированный R-квадрат	-0,026185682
Стандартная ошибка	58,03645994
Наблюдения

 

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		16,22784091	16,22784091	0,004817913	0,945026312
Остаток		127992,7659	3368,230682
Итого		128008,9938

 

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y-пересечение	101,8136364	12,37341483	8,22841856	5,72E-10	76,764967	126,86230	76,7649678	126,8623049
X1	-1,28030303	18,44519779	-0,06941118	0,945026	-38,620653	36,060047	-38,6206534	36,0600474

 

Таким образом, уравнение модели (1) имеете вид:

Коэффициент регрессии b=-1.28, следовательно при изменении города области, в среднем на 1.28 тыс. долл. уменьшается цена квартиры. Свободный член a= 101.813 не имеет экономического смысла, но говорит о том, что сначала меняется фактор X₁, а потом результат Y.

Оценим значимость каждого коэффициента регрессии:

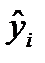- стандартная ошибка, - расчетное значение.

Расчетные значения t-статистик Стьюдента приведены в таблице:

По таблице критических точек распределения Стьюдента (или с помощью функции СТЬЮДРАСПОБР в Excel) при уровне значимости α=5% и числе степеней свободы k=n–2=40–2=38 определим критическое значение: t_кр = 2.024

Таким образом, 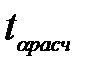> t_кр (8,228>2.024), следовательно свободный член в уравнении регрессии значим; 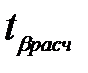< t_кр (-0.069<2.024), следовательно фактор Х₁ в уравнении регрессии не значим, т.е. фактор город области не играет решающую роль в формировании цены на квартиру.

Входной фактор X₂:

Результаты вычислений представлены в таблицах:

Регрессионная статистика
Множественный R	0,75106074
R-квадрат	0,564092234
Нормированный R-квадрат	0,552620977
Стандартная ошибка	38,32002171
Наблюдения

 

 

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		72208,87932	72208,8793	49,17440	2,3659E-08
Остаток		55800,11443	1468,42406
Итого		128008,9938
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y-пересечение	7,539298561	14,67125127	0,513882451	0,6103096	-22,1610966	37,2396937	-22,16109663	37,23969375
X2	36,03776978	5,139115172	7,012446419	2,365E-08	25,63417511	46,4413644	25,63417511	46,44136446

 

Таким образом, уравнение модели (2) имеете вид:

Коэффициент регрессии β=36.037, следовательно при увеличении числа комнат в квартире на 1, в среднем на 36.037 тыс. долл. увеличивается цена квартиры. Свободный член α=7.539 не имеет реального смысла, но показывает, что вначале изменяется фактор X₂, а потом результат Y, т.е. относительное изменение результата происходит медленнее, чем изменение фактора.

Оценим значимость каждого коэффициента регрессии:

Таким образом, 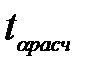< t_кр (0,514<2.024), следовательно свободный член в уравнении регрессии не значим; 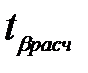> t_кр (7.012>2.024), следовательно фактор Х₂ в уравнении регрессии значим, т.е. число комнат в квартире значительно влияет на стоимость квартиры.

 

Входной фактор X₄:

Результаты вычислений представлены в таблицах:

Регрессионная статистика
Множественный R	0,874012079
R-квадрат	0,763897114
Нормированный R-квадрат	0,75768388
Стандартная ошибка	28,20194696
Наблюдения

 

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		97785,70089	97785,7008	122,9467832	1,79185E-13
Остаток		30223,29286	795,349812
Итого		128008,9938
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y-пересечение	-2,86485154	10,39374857	-0,2756321	0,784323	-23,905895	18,176192	-23,9058953	18,1761922
X4	2,475974588	0,223299421	11,0881370	1,79E-13	2,02392854	2,9280206	2,02392854	2,92802063

 

 

Таким образом, уравнение модели (3) имеете вид:

Коэффициент регрессии β=2.476, следовательно при увеличении жилой площади квартиры на 1 кв. м, в среднем на 2.476 тыс. долл. увеличивается цена квартиры. Свободный член α=-2.865 не имеет экономического смысла, но показывает, что сначала изменяется результат Y, а потом, фактор X₄ т.е. относительное изменение фактора происходит медленнее, чем изменение результата.

Оценим значимость каждого коэффициента регрессии:

Таким образом, 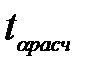< t_кр (-0,275<2.024), следовательно свободный член в уравнении регрессии не значим; 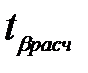> t_кр (11.088>2.024), следовательно фактор Х₄ в уравнении регрессии значим, т.е. фактор жилая площадь квартиры влияет на формирование стоимости квартиры.

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: