Задача 1.7. Оценка качества многофакторной модели

7. Оцените качество построенной модели. Улучшилось ли качество модели по сравнению с однофакторной моделью? Дайте оценку влияния значимых факторов на результат с помощью коэффициентов эластичности, b- и D-коэффициентов.

Для оценки качества выбранной множественной модели (6) , аналогично п.1.4 данной задачи, используем коэффициент детерминации R- квадрат, среднюю относительную ошибку аппроксимации и F -критерий Фишера.

Коэффициент детерминации R -квадрат возьмем из итогов «Регрессии» (таблица «Регрессионная статистика» для модели (6)).

, следовательно, вариация (изменение) цены квартиры Y на 76,77% объясняется по данному уравнению вариацией города области Х₁, числа комнат в квартире Х₂ и жилой площади Х₄.

Используем исходные данные Y_i и найденные инструментом «Регрессия» остатки (таблица «Вывод остатка» для модели (6)). Рассчитаем относительные погрешности и найдем среднее значение .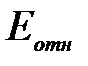

ВЫВОД ОСТАТКА

Наблюдение	Предсказанное Y	Остатки	Отн. погрешность
	45,95089273	-7,95089273	20,92340192
	86,10296493	-23,90296493	38,42920407
	94,84442678	30,15557322	24,12445858
	84,17648426	-23,07648426	37,76838667
	40,2537216	26,7462784	39,91981851
	68,70572376	24,29427624	26,12287768
	143,7464899	-25,7464899	21,81905923
	106,0907598	25,90924022	19,62821228
	135,357993	-42,85799303	46,33296544
	114,4792566	-9,47925665	9,027863476
	41,48765602	0,512343975	1,219866607
	103,2329236	21,76707636	17,41366109
	130,3567798	39,64322022	23,3195413
	35,41901876	2,580981242	6,7920559
	155,4129693	-24,91296925	19,0903979
	84,32108188	0,678918123	0,798727204
	98,0552279	-0,055227902	0,056355002
	144,2104618	-16,21046182	12,66442329
	122,8677535	-37,86775351	44,55029825
	100,0221225	59,97787748	37,48617343
	53,27196558	6,728034423	11,21339071
	35,06605378	5,933946225	14,47303957
	114,4792566	-24,47925665	27,19917406
	113,1343153	-30,13431529	36,30640396
	40,43190991	4,568090093	10,15131132
	39,34427892	-0,344278918	0,882766457
	144,4794501	-57,57945009	66,25943623
	56,4827667	-16,4827667	41,20691675
	95,38240332	-15,38240332	19,22800415
	228,6988826	-1,698882564	0,748406416
	222,8067278	12,19327221	5,188626473
	38,81483144	1,185168555	2,962921389
	48,36325811	18,63674189	27,81603267
	126,6080021	-3,608002113	2,933335051
	84,85052935	15,14947065	15,14947065
	116,7991162	-11,79911625	11,23725357
	84,17648426	-13,87648426	19,73895342
	113,9412801	-31,94128011	38,95278062
	215,494184	64,50581599	23,03779142
	141,7795953	58,22040472	29,11020236
Среднее	101,2375		22,51770962

 

По столбцу относительных погрешностей найдем среднее значение 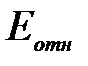=22.51% (с помощью функции СРЗНАЧ).

Сравнение показывает, что 22.51%>7%. Следовательно, точность модели неудовлетворительная.

С помощью F – критерия Фишера проверим значимость модели в целом. Для этого выпишем из итогов применения инструмента «Регрессия» (таблица «дисперсионный анализ» для модели (6)) F= 39,6702.

С помощью функции FРАСПОБР найдем значение F_кр=3.252 для уровня значимости α = 5%, и чисел степеней свободы k₁ = 2, k₂ = 37.

F>F_кр, следовательно, уравнение модели (6) является значимым, его использование целесообразно, зависимая переменная Y достаточно хорошо описывается включенными в модель (6) факторными переменными Х ₁, Х ₂. и Х ₄.

Дополнительно с помощью t–критерия Стьюдента проверим значимость отдельных коэффициентов модели.

t –статистики для коэффициентов уравнения регрессии приведены в итогах инструмента «Регрессия». Получены следующие значения для выбранной модели (6) :

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y-пересечение	-5,643572321	12,07285417	-0,46745966	0,642988	-30,1285	18,84131	-30,1285	18,84131
X4	2,591405557	0,461440597	5,61590284	2,27E-06	1,655561	3,52725	1,655561	3,52725
X1	6,85963077	9,185748512	0,74676884	0,460053	-11,7699	25,48919	-11,7699	25,48919
X2	-1,985156991	7,795346067	-0,25465925	0,800435	-17,7949	13,82454	-17,7949	13,82454

 

Критическое значение t_кр найдено для уровня значимости α=5% и числа степеней свободы k=40–2–1=37. t_кр=2.026 (функция СТЬЮДРАСПОБР).

Для свободного коэффициента α=–5.643 определена статистика 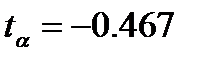, 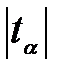<t_кр, следовательно, свободный коэффициент не является значимым, его можно исключить из модели.

Для коэффициента регрессии β₁=6.859 определена статистика 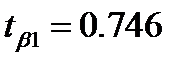, <t_кр, следовательно, коэффициент регрессии β₁ не является значимым, его и фактор города области можно удалить из модели.

Для коэффициента регрессии β₂=-1,985 определена статистика , <t_кр, следовательно, коэффициент регрессии β₂ не является значимым, его и фактор числа комнат в квартире можно исключить из модели.

Для коэффициента регрессии β₄=2.591 определена статистика , >t_кр, следовательно, коэффициент регрессии β₄ является значимым, его и фактор жилой площади квартиры можно сохранить в модели.

Выводы о значимости коэффициентов модели сделаны на уровне значимости α=5%. Рассматривая столбец «P-значение», отметим, что свободный коэффициент α можно считать значимым на уровне 0.64 = 64%; коэффициент регрессии β₁ – на уровне 0,46 = 46%; коэффициент регрессии β₂ – на уровне 0,8 = 80%; а коэффициент регрессии β₄ – на уровне 2,27E-06= 2,26691790951854E-06 = 0,0000002%.

При добавлении в уравнение новых факторных переменных автоматически увеличивается коэффициент детерминации R² и уменьшается средняя ошибка аппроксимации, хотя при этом не всегда улучшается качество модели. Поэтому для сравнения качества модели (3) и выбранной множественной модели (6) используем нормированные коэффициенты детерминации.

Модель	Нормированный R-квадрат
(3)	0,757683880132941
(6)	0,748404306989435

 

Таким образом, при добавлении в уравнение регрессии фактора «город области» Х ₁ и фактора «число комнат в квартире» Х ₂ качество модели ухудшилось, что говорит в пользу удаления факторов Х ₁ и Х ₂ из модели.

Проведем дальнейшие расчеты.

Средние коэффициенты эластичности в случае линейной модели определяются формулами .

С помощью функции СРЗНАЧ найдем: =0.45, =2.6, =42.05, =101.24.

Тогда , ,

Следовательно, увеличение жилой площади Х₄ при том же кол-ве комнат и городе области на 1% приводит к увеличению цены квартиры в среднем на 1,076%.

При изменении города области (Х₁) и неизменной жилой площади и числе комнат в квартире цена квартиры увеличится в среднем на 0,03%.

При изменении числа комнат в квартире (Х₂) и неизменной жилой площади и городе области цена уменьшается в среднем на 0,05%.

 

Бета-коэффициенты определяются по формулам: ,

где среднее квадратическое отклонение j – го фактора - .

,

С помощью функции СТАНДОТКЛОН найдем S_X1= 0,504, S_X2= 1,194, S_X4=20.223; S_Y= 57,291.

Тогда ; ;

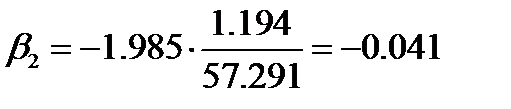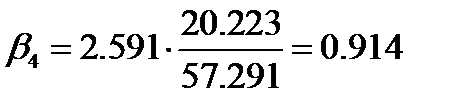
Таким образом, при увеличении только фактора Х₁ на одно свое стандартное отклонение результат Y увеличивается в среднем на 0.06 своего стандартного отклонения S_Y, при увеличении только фактора Х₂ на одно его стандартное отклонение – уменьшается на 0,041 S_Y, при увеличении только фактора Х₄ на одно его стандартное отклонение – увеличивается на 0,914 S_Y

Дельта-коэффициенты определяются формулами .

Найдем коэффициенты парной корреляции с использованием инструмента «Корреляция» пакета «Анализ данных» в Excel.

	Y	X1	X2	X4
Y
X1	-0,01126
X2	0,751061	-0,0341
X4	0,874012	-0,0798	0,868524

 

Коэффициент детерминации был определен ранее и равен 0.7677.

Вычислим дельта-коэффициенты:

;

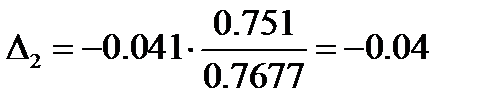
Поскольку Δ₁<0 и Δ₂<0, то факторные переменные Х₁ и Х₂ выбрана неудачно, и их нужно удалить из модели. Значит, по уравнению полученной линейной трехфакторной модели изменение результирующего фактора Y (цены квартиры) на 104% объясняется воздействием фактора Х₄ (жилой площадью квартиры), на 4% воздействием фактора Х₂ (число комнат), на 0,0859% воздействием фактора Х₁ (город области).

⇐ Предыдущая12345

Поделиться:

Воспользуйтесь поиском по сайту: