 |
Расчет скорости витания (осаждения) и уноса
|
|
|
|
При скорости потока 
порозность приближается к единице. Поэтому можно рассматривать взаимодействие потока жидкости
и отдельной частицы. Скорость соответствует верхней границе режима псевдоожижения, при этом частица неподвижно витает в потоке. Эту скорость называют скоростью витания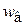 
. Для случая витания вес частицы полностью уравновешивается силовым воздействием жидкостного потока. Этот случай силового взаимодействия реализуется
и для случая, когда твердая частица падает с постоянной скоростью 
, называемой скоростью осаждения, в неограниченном объеме неподвижной среды. Следовательно = .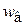
При ламинарном обтекании тела сопротивление потока зависит
в основном от вязкости среды; при турбулентном – от поверхности
тела отрываются вихри, которые создают за ним область пониженного давления (рис. 3.4).
а) б)
Рис. 3.4. Обтекание потоком сферы:
а – ползущее течение; б – отрыв пограничного слоя
Рассмотрим осаждение сферической частицы диаметром 
. Запишем условие равновесия сил:
(3.21)
где 
– сила сопротивления потока, 
– вес частицы, 
– выталкивающая (архимедова) сила. Силу можно выразить по аналогии с потерянным давлением с использованием коэффициента гидравлического сопротивления x:
(3.22)
где S – площадь поперечного сечения сферы 
, r – плотность среды, x – коэффициент гидравлического сопротивления.
Для сферы очевидно:
(3.23)
где 
– плотность твердой частицы. Тогда получим:
(3.24)
Из (3.24) найдем значение 
:
(3.25)
Рассмотрим более подробно коэффициент гидравлического сопротивления x. Силу сопротивления потока можно представить в виде суммы сил лобового сопротивления 
и сопротивления трения 
:
(3.26)
Тогда и коэффициент гидравлического сопротивления x может быть выражен зависимостью:
|
|
|
(3.27)
где 
– коэффициент лобового сопротивления, 
– коэффициент сопротивления трения.
При ламинарном течении частица плавно обтекается потоком жидкости (ползущее течение) и энергия расходуется только
на преодоление трения. С увеличением скорости потока всё большую роль играет лобовое сопротивление, и с какого-то момента сопротивлением трения можно будет пренебречь. Тогда увеличение скорости потока
не приведет к изменению , наступает автомодельный режим (рис. 3.5).
Рис. 3.5. Зависимость коэффициента гидравлического сопротивления x
от режима обтекания сферы
Для случая ламинарного режима осаждения можно получить теоретическим путем значение x:
(3.28)
Тогда из (3.35) получим:
(3.29)
Полученная зависимость называется законом осаждения Стокса. Закон Стокса справедлив для области 
. В области действия закона Ньютона (в условиях автомодельности критерия 
) коэффициент гидравлического сопротивления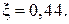 
Тогда из (3.25) будем иметь:
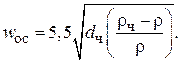(3.30)
В промежуточной области 
для x предлагается следующая формула:
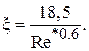(3.31)
Для того чтобы определить режим обтекания частицы потоком жидкости и, следовательно, выбрать формулу для расчета скорости , необходимо знать величину , а содержит искомую величину . Задачу можно решить методом последовательных приближений. Однако этого трудоемкого процесса можно избежать. Преобразуем уравнение (3.25), вводя критерии и Ar, и получим:
(3.32)
Из (3.32) определим границы промежуточной зоны по критерию Архимеда Ar:
для 
получим Ar = 36;
для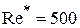 
получим Ar = 8,3 · 104.
Как известно, критерий Архимеда не содержит искомую величину .
Тогда можно предложить следующий порядок расчета скорости витания (осаждения):
– определяем значения критерия Архимеда Ar;
– определяем зону расчета x и выбираем расчетную формулу;
– для данной зоны по соответствующей формуле определяем значение скорости .
|
|
|
Скорость осаждения частиц несферической формы 
меньше, чем у сферических частиц:
w 'ос = jф w ос.
Здесь jф < 1 – коэффициент формы, значение которых определяется опытным путем. Например, для округлых частиц jф = 0,77, угловатых –
jф = 0,66, продолговатых – jф = 0,50 и пластинчатых – jф = 0,46. Коэффициент формы связан с фактором формы соотношением jф = f–2.
Скорость стесненного осаждения меньше скорости одиночной частицы за счет соударения твердых частиц друг о друга.
Для приближенного определения при всех режимах движения частиц можно использовать универсальную формулу Тодеса:
(3.33)
При скоростях потока жидкости, превышающих критическую скорость 
, происходит разрушение псевдоожиженного слоя и вынос частиц из аппарата. Скорость потока, при которой происходит массовый унос твердых частиц из аппарата, называют скоростью уноса 
. Скорость уноса всегда больше скорость витания 
.
Осаждение твердых частиц под действием центробежных сил. Осаждение твердых частиц под действием центробежных сил происходит более интенсивно. Интенсивность осаждения оценивается фактором разделения 
как отношение центробежной силы 
к силе тяжести 
:
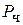(3.34)
где w – угловая скорость вращения, r – радиус вращения. Для расчета центробежной скорости осаждения применяют те же формулы, что и для осаждения в поле сил тяжести, но с учетом фактора разделения:
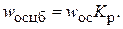(3.35)
Исходное критериальное уравнение для этого случая имеет вид:
(3.36)
C учетом уравнения (3.36) устанавливаются зоны центробежного осаждения:
|
|
|
