 |
Расчет сложных трубопроводов
|
|
|
|
Параллельное соединение трубопроводов. Трубопровод
в некоторой точке А разветвляется на несколько труб, которые соединяются в точке В (рис. 2.25). Расход основного трубопровода
до деления и после объединения один и тот же.
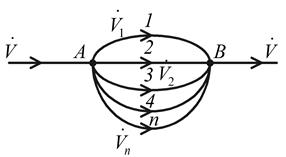
Рис. 2.25. Схема параллельного соединения трубопроводов
Основная задача для этого случая: определить 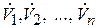 и потери напора на участке
и потери напора на участке  . Поскольку напор в точках А и В общий для всех ветвей, то потери напора для всех ветвей будут одинаковыми
. Поскольку напор в точках А и В общий для всех ветвей, то потери напора для всех ветвей будут одинаковыми
и равными  .
.
Запишем потери напора для первой ветви:
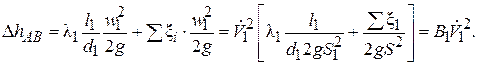
Аналогично для других ветвей:
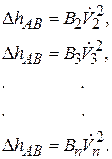 (2.72)
(2.72)
Всего имеем n уравнений (по числу веток трубопровода). Но в этих уравнениях число неизвестных n + 1. Ещё одно уравнение получим, записав постоянство расхода для основного трубопровода и суммарного расхода в зоне ветвей:
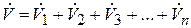 . (2.73)
. (2.73)
Из системы уравнений (2.72) определим все расходы через 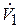 :
:
 (2.74)
(2.74)
Решая совместно уравнения (2.73) и (2.74), получим:
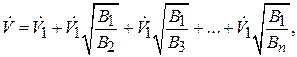
откуда расход первой ветви 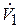 :
:
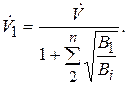 (2.75)
(2.75)
Уравнение (2.75) позволяет определить все неизвестные величины. По уравнениям (2.74) находим 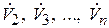 , а по (2.72) –
, а по (2.72) –  . Приведенное решение задачи предполагает использование квадратичного закона сопротивлений.
. Приведенное решение задачи предполагает использование квадратичного закона сопротивлений.
Непрерывная раздача расхода по пути. Рассмотрим непрерывную раздачу расхода на некотором участке трубопровода AB длиной l
(рис. 2.26).

Рис. 2.26. Схема непрерывной раздачи расхода по пути
Основная задача – определение потери давления на этом участке D p. Точное решение задачи связано с теорией движения жидкости
с переменным расходом (Мещерский, Петров). Здесь предлагается приближенное инженерное решение. Обозначим: 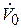 – общий расход
– общий расход
до раздачи; 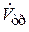 – транзитный расход после участка раздачи; q – удельный расход единицы длины;
– транзитный расход после участка раздачи; q – удельный расход единицы длины; 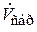 – сбросный расход на участке АВ. Тогда имеем:
– сбросный расход на участке АВ. Тогда имеем:
|
|
|
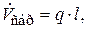
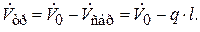
В сечении n – n на расстоянии х от узла А расход равен:
 (2.76)
(2.76)
Запишем уравнение Бернулли для участка длиной dx
в дифференциальной форме с учетом потери напора 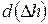 :
:

Считаем, что dz и 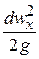 по сравнению с остальными членами уравнения незначительны, а потеря напора D h определяется
по сравнению с остальными членами уравнения незначительны, а потеря напора D h определяется
по формуле Дарси – Вейсбаха. Тогда для потери давления на участке длиной 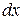 получим:
получим:
 (2.77)
(2.77)
Здесь 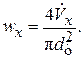
Тогда получим:
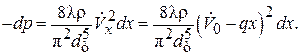 (2.78)
(2.78)
Пределы интегрирования: по давлению от  до
до  , длине от
, длине от 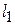 до
до 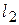 :
:
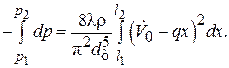 (2.79)
(2.79)
Проводя интегрирование и имея в виду, что  ,
, 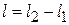 , получим:
, получим:
или 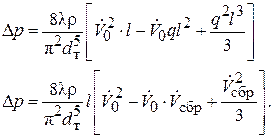 (2.80)
(2.80)
В частном случае, если 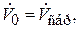 получим:
получим:
 (2.81)
(2.81)
Эта формула показывает, что в случае полной непрерывной раздачи расхода из трубопровода потеря давления в три раза меньше того, который имел бы место при отсутствии раздачи, т.е. при полном транзите.
По полученной зависимости определяем или D p, или 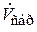 .
.
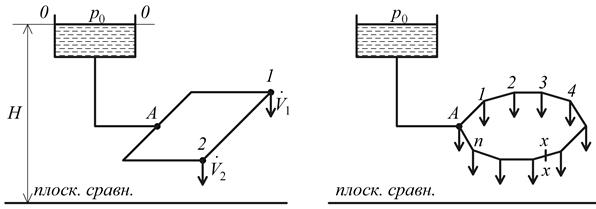
Кольцевой трубопровод. Схемы кольцевых трубопроводов представлены на рис. 2.27. Основной расчетной задачей является определение необходимого напора Н в условиях, когда заданы расходы
в точках отбора 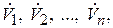 расположение трубопроводов
расположение трубопроводов  длины отдельных участков и диаметры всех труб.
длины отдельных участков и диаметры всех труб.
а) б)
Рис. 2.27. Схемы кольцевых трубопроводов:
а – с двумя узловыми точками; б – общий случай
Рассмотрим простейший случай а – с двумя узловыми точками расхода  и
и  . Трудность заключается в том, что на участке 1–2 неизвестно направление движения жидкости.
. Трудность заключается в том, что на участке 1–2 неизвестно направление движения жидкости.
Если  , то
, то 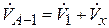 ,
,
 , точка схода 2.
, точка схода 2.
Если  , то
, то 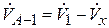 ,
,
 , точка схода 1.
, точка схода 1.
В любом случае потери напора от точки А до точки схода одинаковы по обоим направлениям:
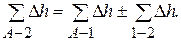 (2.82)
(2.82)
Уточняем направление 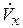 на участке 1–2. Для этого воспользуемся уравнением Дарси – Вейсбаха.
на участке 1–2. Для этого воспользуемся уравнением Дарси – Вейсбаха.
Предположим, что местные гидравлические сопротивления незначительны. Тогда имеем:
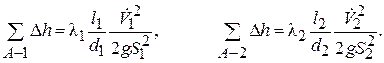
Здесь 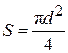 – площадь живого сечения трубопровода.
– площадь живого сечения трубопровода.
Если  , то
, то 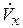 от
от  , точка схода 1.
, точка схода 1.
Если  , то
, то 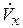 от
от  , точка схода 2.
, точка схода 2.
Пусть точка схода 2. Тогда можно записать:
|
|
|
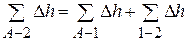
или  (2.83)
(2.83)
Здесь  ,
, 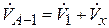 . По уравнению (2.83) определяем значение
. По уравнению (2.83) определяем значение 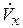 .
.
Далее запишем уравнение Бернулли для сечения 0–0 и точки схода 2:
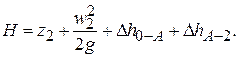 (2.84)
(2.84)
Здесь  ,
, 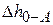 – определяется по полному расходу для всей системы,
– определяется по полному расходу для всей системы, 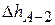 – по
– по 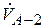 .
.
Для общего случая б алгоритм расчета такой же. Где-то надо разорвать кольцо, предположим в сечение х–х, и необходимо проверить потери напора:
 . (2.85)
. (2.85)
Остальное по аналогии с а.
Разветвленная сеть трубопроводов (рис. 2.28). Предположим,
что известны необходимые расходы в точках 1, 2,…, n и их местоположение в пространстве  , а также свободный напор
, а также свободный напор
в точках потребления 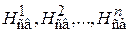 . Свободный напор в точках потребления обеспечивает работу какого-либо технологического аппарата, т.е.
. Свободный напор в точках потребления обеспечивает работу какого-либо технологического аппарата, т.е.  обеспечивает потери напора в аппарате.
обеспечивает потери напора в аппарате.
Необходимо найти потребный напор Н, обеспечивающий работу всей системы. Начнем с определения магистральной линии.
За магистральную линию обычно принимают самую длинную линию, включающую наибольшие сопротивления и пропускающую наибольшее количество жидкости.
Потребный напор сети определяется как полная потеря напора
по всей магистральной линии, складывающаяся как сумма потерь напора на участках этой линии, разности начала и конца магистральной линии
и свободного напора в конце магистральной линии.
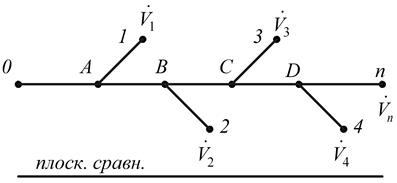
Рис. 2.28. Схема разветвления трубопровода
Предположим, что магистральная линия 0 – А – В – С – D – n. Запишем уравнение Бернулли для сечений 0 и n:
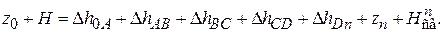 (2.86)
(2.86)
Будем считать, что на отдельных участках 0 А, АВ и т.д. трубопроводы постоянного диаметра, коэффициент гидравлического сопротивления l учитывает и местные потери напора.
Рассмотрим участок 0 А.
Расход 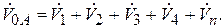
Принимая скорость в пределах 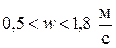 , задаемся d
, задаемся d
и определяем значение l.
По формуле Дарси – Вейсбаха находим 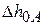 :
:
 (2.87)
(2.87)
Аналогично определяем потери напора на отдельных участках. Таким образом, по формуле (2.86) находим потребный напор для системы Н.
Определяем напор в точках ответвления.
Точка А: 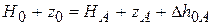 . Находим HA.
. Находим HA.
Точка В: 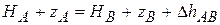 . Находим HB и т.д.
. Находим HB и т.д.
Для остальных точек ответвления аналогичны.
Рассмотрим ответвление, например А 1.
Для начала и конца ответвления запишем уравнение Бернулли:
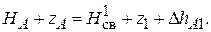 (2.88)
(2.88)
Из формулы (2.88) находим  и далее определяем необходимый диаметр трубы на ответвлении А 1. Остальные участки анализируются аналогично.
и далее определяем необходимый диаметр трубы на ответвлении А 1. Остальные участки анализируются аналогично.
|
|
|
Для разветвленных трубопроводов возможны и другие задачи.
Сифонный трубопровод
Сифонным трубопроводом называется такой трубопровод, часть которого располагается выше уровня жидкости в сосуде, из которого происходит подача жидкости. Сифон работает самотечно, над вакуумом (рис. 2.29). Движение жидкости в сифоне происходит за счет разницы высот уровней сосудов А и В:
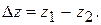
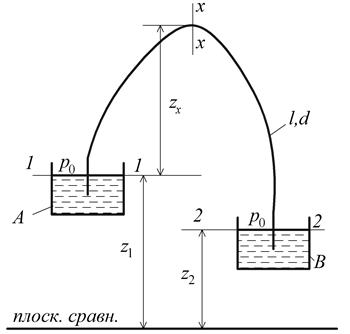
Рис. 2.29. Схема сифонного трубопровода
Наличие вакуума в трубопроводе вызывает выделение растворенного в жидкости газа, а при значительном вакууме может привести
к интенсивному испарению жидкости. Поэтому нормальная работа сифонного трубопровода возможна только до давления насыщенного пара перекачиваемой жидкости при данной температуре  . Это минимальное давление определяется для самой верхней точки сифонного трубопровода (по схеме для сечения х–х). Итак, условия нормальной работы сифона:
. Это минимальное давление определяется для самой верхней точки сифонного трубопровода (по схеме для сечения х–х). Итак, условия нормальной работы сифона: 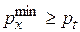 .
.
При расчете сифона сначала определяют его расход, затем проверяют на работоспособность. Итак, определяем расход сифона.
Для этого запишем уравнение Бернулли для сечения 1–1 и 2–2:
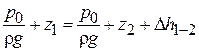 ,
, 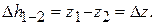
С другой стороны, определим  с помощью уравнений Дарси – Вейсбаха:
с помощью уравнений Дарси – Вейсбаха:
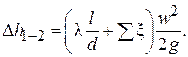
Далее, переходя к расходу 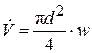 , найдем:
, найдем:
 (2.89)
(2.89)
Проверяем работоспособность сифона. Запишем уравнение Бернулли для сечений 1–1 и х–х (наивысшее живое сечение сифона):
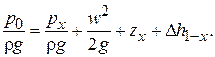 (2.90)
(2.90)
Из уравнения (2.90) найдем  :
:
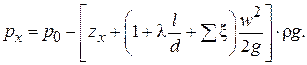 (2.91)
(2.91)
Давление насыщенного пара жидкости  зависит от температуры,
зависит от температуры,
с ростом температуры  растет. В летних условиях для воды
растет. В летних условиях для воды 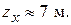
|
|
|


