 |
Лекция 53. Колебательное движение. Физические величины, которые характеризуют колебательное движение
|
|
|
|
Цели: познакомить студентов с величинами, характеризующими колебательное движение, выяснить от чего зависит период колебаний
Тип занятия: изучение нового материала.
План занятия
1. Актуализация знаний
2. Колебательное движение
3. Характеристики колебаний
ХОД ЗАНЯТИЯ
I. Организационный момент
Объявление темы и цели занятия. (Cлайд 1)
II. Актуализация опорных знаний
Фронтальный опрос: продолжите фразу: (Слайды 2, 3)
1. Движение, при котором тело откланяется то в одну то в другую сторону, называется …
2. Основной признак …
3. Колеблется тело на нити или тело на пружине …
4. Математическим маятником называется …
5. Колебания, происходящие только благодаря начальному запасу энергии, называются …
6. Свободно колеблющиеся тела взаимодействуют с другими телами и вместе с ними образуют систему тел, которая называется …
7. Одно из основных общих свойств колебательных систем заключается в …
Выберите правильный ответ: (Слайд 4)
1. Какие из перечисленных ниже движений являются механическими колебаниями?
А. Движение качелей.
Б. Движение мяча, падающего на землю.
В. Движение звучащей струны гитары
2. Свободными называют колебания, которые происходят под действием…
А. … силы трения
Б. … внешних сил
В. … внутренних сил
Беседа (Слайд 5)
1. Как вы понимаете утверждение, что колебательное движение периодично?
2. Какой общей чертой (кроме периодичности) обладают движения тел, изображенных на рис. 48, стр. 87.
3. Какие тела входят в колебательную систему, называемую пружинным маятником?
III. Основная часть. Изучение нового материала
Демонстрации колебаний тела на пружине и на нити. Введем основные характеристики колебательного движения: амплитуда, период, частота и фаза колебаний: (Слайд 6)
|
|
|
Амплитуда – максимальное отклонение относительно положения равновесия (А, м)
Период – время полного колебания (Т, с)
Частота – число колебаний за единицу времени (v, Гц)
Фаза колебания – угловая мера времени
Формулы: (Слайд 7)
Т = 1/ v; Т = t/n – период { с }
v = 1/Т; v = n/t – частота { Гц }
А – амплитуда { м }
 – фаза { рад }
– фаза { рад }
Решение задач
1. Определить период и частоту материальной точки, совершающей 50полных колебаний за 20 с.
2. Сколько колебаний совершит материальная точка за 5с при частоте колебаний 440 Гц.
Перед классом ставится задача: выяснить, от чего зависит период колебаний математического маятника. Разбивается класс на 3 группы «экспериментаторов». (Слайд 9) Каждая руппа получает задание:
Задание для группы 1. Определить опытным путем зависит ли период колебаний математического маятника от его массы.
Оборудование: штатив с муфтой, нить, набор грузов, секундомер.
Задание для группы 2. Определить, зависит ли период колебаний математического маятника от амплитуды колебаний.
Оборудование: штатив с муфтой, маятник произвольной длины, транспортир, секундомер.
Задание для группы 3. Определить, зависит ли период колебаний математического маятника от его длины.
Оборудование: штатив с муфтой, маятник произвольной длины, сантиметровая лента, секундомер.
Далее, один из студентов каждой группы рассказывает о проведенных опытах и записывает результаты опытов на доске в таблицу:
| № опыта | длина, м | масса, кг | период, с |
| № опыта | длина, м | амплитуда, м | период, с |
| № опыта | длина, м | масса, кг | период, с |
| 0,1 | |||
| 0,1 |
Студенты самостоятельно приходят к выводу: период колебаний математического маятника не зависит от массы тела, не зависит от амплитуды колебаний, а зависит только от длины математического маятника.
|
|
|
Контрольные вопросы
1. От чего зависит период колебаний математического маятника:?
2. Характеристики колебательного движения?
3. От чего зависит период колебаний математического маятника
Домашнее задание: § 26, упр. 24 (2, 3, 4).
Список использованной литературы
1. Физика. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни / Г. Я. Мякишев, Б. Б. Буховцев, Н. Н. Сотский; под ред. В. И. Николаева, Н. А. Парфентьевой. — 19-е изд. — М.: Просвещение, 2010. — 366 с.: ил.
2. Марон А.Е., Марон Е.А. «Сборник задачорник качественных задач по физике 11 кл, М.: Просвещение,2006
3. Л.А. Кирик, Л.Э.Генденштейн, Ю.И.Дик. Методические материалы для преподавателя 10 класс,М.:Илекса, 2005.-304с:, 2005
4. Л.Э.Генденштейн, Ю.И.Дик. Физика 11 класс.-М.: Мнемозина,2010
Лекция 54. Гармонические колебания. Математический маятник. Пружинный маятник. Энергия колебательного движения. Вынужденное колебание. Резонанс. Автоколебания
План занятия
1. Понятие гармонических колебаний.
2. Математический маятник
2.1 Зависимость периода колебаний математического маятника от массы подвешенного груза
2.2. Зависимость периода колебаний математического маятника от длины подвеса
3. Решение задач
ХОД ЗАНЯТИЯ
1 Организационный момент
1.1 Приветствие студентов.
Преподаватель здоровается с присутствующими.
1.2 Подготовка аудитории к занятию, проверка присутствующих
Преподаватель проверяет присутствие студентов группы на занятии, готовность к занятию.
1. Актуализация опорных знаний
Актуализация проводится в виде фронтального опроса для подгруппы студентов и решения задач для второй части группы. (Приложение А)
Актуализация знаний сопровождается презентацией
(Слайды 2-7, Приложение Б)
2.1.Что такое механические колебания? (Слайд 3, приложение Б)
Ожидаемый ответ: Это движения, которые точно или приблизительно повторяются через определённый промежуток времени.
Какие колебания называют свободными? (Слайд 4, приложение Б)
Ожидаемый ответ: Колебания, происходящие в отсутствие внешнего воздействия.
Какие колебания называют вынужденными?
Ожидаемый ответ: Колебания, происходящие под воздействием внешних периодических сил.
|
|
|
Какие величины характеризуют колебательное движение? (Слайд 5, приложение Б)
Ожидаемый ответ: Период, частота, циклическая частота и фаза колебаний.
2.2. Взаимопроверка расчетных работ студентов. Выставление оценок согласно критериям оценивания, которые представлены на презентации. (Слайд 6-7, приложение Б)
2.3. Комментирование ответов студентов по фронтальному опросу
3. Мотивация
Мотивация (сопровождается видеофрагментом №1).
Для мотивирования студентов к изучению темы занятия демонстрируется видеоролик.
После просмотра видео, студенты должны ответить на поставленный преподавателем вопрос: «Что объединяет все продемонстрированные видеофрагменты?»
Ожидаемый ответ: На каждом из отрывков видео продемонстрированы механические колебания.
В нашей жизни мы всюду встречаемся с колебательными движениями: периодически движутся участки сердца и легких, колеблются ветви деревьев при порыве ветра, ноги и руки при ходьбе, колеблются струны гитар, колеблется спортсмен на батуте и школьник, пытающийся подтянуться на перекладине, пульсируют звезды (будто дышат), колеблются атомы в узлах кристаллической решетки.
С данными процессами связана тема нашей лекции: «Гармонические колебания. Математический маятник». (Слайд 9, приложение Б)
(Студенты записывают тему лекции)
Студентам предлагается самостоятельно поставить цель занятия, исходя из темы и просмотренных видеофрагментов.
Студенты формируют цель занятия, преподаватель повторно оглашает поставленную цель. (Слайд 10, приложение Б)
Цели занятия: Изучить процесс колебания математического маятника, сформировать представление о гармонических колебаниях.
3. Изложение нового материала
Преподаватель предлагает ознакомиться студентов с планом занятия. (Слайд 11, приложение Б)
Изложение материала преподавателем сопровождается презентацией (Слайды 11-17, приложение Б)
1. Понятие гармонических колебаний. (Рассказ преподавателя)
Одним из видов колебательного процесса являются гармонические колебания, которые описываются уравнением
|
|
|
x = xm cos (ω t + φ0).
Здесь x – смещение тела от положения равновесия,
xm – амплитуда колебаний, то есть максимальное смещение от положения равновесия,
ω – циклическая или круговая частота колебаний,
t – время.
График гармонических колебаний представляет собой синусоиду или косинусоиду. (Слайд 12, приложение Б)
Во всех трех случаях для синих кривых φ0 = 0:

Рис. 1 Пример графика колебаний с разной амплитудой
Красная кривая отличается от синей только большей амплитудой (x'm > xm);

Рис. 2 Пример графика колебаний с разным значением периода
Красная кривая отличается от синей только значением периода (T' = T / 2);
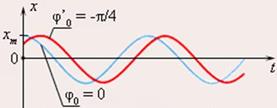
Рис. 3 Пример графика колебаний с разным значением начальной фазы колебаний
Красная кривая отличается от синей только значением начальной фазы (рад). (Слайд 13, приложение Б)
Механические колебания маятника тоже являются гармоническими.
 Студентами демонстрируется видео, демонстрирующее синусоидальную развертку колебаний. (Видеофрагмент №2)
Студентами демонстрируется видео, демонстрирующее синусоидальную развертку колебаний. (Видеофрагмент №2)
Комментирование выступления студентов.
2. Математический маятник ( Рассказ преподавателя )
Математическим маятником называют тело небольших размеров, подвешенное на тонкой нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела.
Реальной моделью математического маятника в опытах будет служить небольшой шарик, подвешенный на тонкой упругой нити. Размеры шарика должны быть малы по сравнению с длиной нити. Это дает возможность считать, что вся масса сосредоточена в одной точке, в центре тяжести шарика.
В положении равновесия, когда маятник
висит по отвесу, сила тяжести уравновешивается силой натяжения нити Т.
При отклонении маятника из положения равновесия на некоторый угол φ появляется касательная составляющая силы тяжести Fτ = –mg sin φ.
Знак «минус» в этой формуле означает, что касательная составляющая направлена в сторону, противоположную отклонению маятника. (Слайд 14, приложение Б)
Период колебаний математического маятника рассчитывается по формуле:


Здесь
l- длина подвеса маятника;
g- ускорение свободного падения.
2.1 Зависимость периода колебаний математического маятника от массы подвешенного груза (Слайд 15, приложение Б)
Студентами демонстрируется ранее подготовленный видео-опыт, который доказывает независимость периода колебаний математического маятника от массы подвешенного груза. (Видеофрагмент №2)
2.2. Зависимость периода колебаний математического маятника от длины подвеса (Слайд 16, приложение Б)
Студентом демонстрируется в аудитории опыт, который доказывает прямопропорциональную зависимость периода колебаний математического маятника от длины подвеса. Студент комментирует результаты опыта.
|
|
|
Преподаватель комментирует ответы студентов и обобщает ответы студентов. (Слайд 17, приложение Б)
|
|
|


