 |
Процессы всасывания и нагнетания поршневых насосов
|
|
|
|
Процесс всасывания. Особенность всасывания поршневого насоса, в отличие от центробежного, заключается в том, что скорость движения жидкости во всасывающей трубе не остается постоянной с течением времени. Она изменяется пропорционально переменной скорости движения поршня. Из графика на рис. 6.27, а видно, что в первую половину хода поршня скорость его увеличивается от нуля до максимума, во вторую – уменьшается от минимума до нуля.
При нормальной работе насоса всасываемая жидкость неразрывно следует за поршнем. Поэтому в первую половину хода поршня жидкость во всасывающей трубе движется ускоренно, а во вторую – замедленно.
Часть напора 
, соответствующего давлению на свободной поверхности питательного бака (рис. 6.23), в первую половину хода поршня затрачивается на сообщение жидкости ускорения. Благодаря этому разрежение под поршнем увеличивается. Во второй половине хода поршень наоборот движется замедленно, с отрицательным ускорением, жидкость тормозится замедляющим своё движение поршнем, и давление под поршнем возрастает. На рис. 6.28 представлена схема всасывающей линии поршневого насоса.
Рис. 6.28. Схема всасывающей линии поршневого насоса
Запишем уравнение Бернулли для сечений 0–0 и х – х:
(6.63)
Здесь 
– давление на свободной поверхности питательного бака, 
– давление в полости насоса, 
– высота всасывания, 
– скорость движения поршня, 
– суммарные гидравлические потери всасывающей линии, 
– гидравлические сопротивления всасывающего клапана, 
– напор, затрачиваемый на преодоление инерционного сопротивления жидкости благодаря неустановившемуся характеру ее движения во всасывающей линии.
Рассмотрим каждый член уравнения (6.63) в отдельности.
|
|
|
Довольно часто 
. В химической технологии встречаются случаи, когда питательный бак закрыт. В этом случае с течением времени давление будет уменьшаться. Предполагая, что объем воздуха над жидкостью в питательном баке 
меняется по изотерме, получим формулу для расчета давления :
(6.64)
где 
– первоначальное давление воздуха над жидкостью, – первоначальный объем воздуха над жидкостью, 
– подача насоса, 
– время наблюдения.
Давление должно быть меньше давления , иначе не будет всасывания. Чем меньше , тем лучше условия для всасывания. Нижний предел давления обусловлен кавитацией. Если 
(давление парообразования жидкости при данной температуре), будет кавитация
и наступит ударная работа насоса. Поршень в момент всасывания оторвется от жидкости, и в начале нагнетания произойдет удар поршня
о жидкость. Следовательно, крайнее значение 
.
Высота всасывания в уравнении (6.63) является искомой величиной. Скоростной напор поршня 
меняется по закону синуса:
w п2/2g = (w r sinj)2/2g. (6.65)
Так как жидкость во всасывающей трубе движется непрерывно вслед за поршнем, то исходя из условия неразрывности потока получим выражение для скорости жидкости во всасывающей трубе:
Определим суммарное гидравлическое сопротивление всасывающей линии :
(6.66)
Как видно из выражения (6.66), , как и скоростной напор поршня, меняется по закону синуса.
Гидравлическое сопротивление всасывающего клапана 
определяется по формуле:
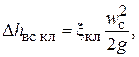(6.67)
где 
– коэффициент сопротивления клапана, 
– скорость жидкости при прохождении через седло клапана. Скорость определяется
из условия неразрывности:
где 
– площадь поперечного сечения седла. Тогда получим:
(6.68)
Как видно из выражения (6.68), 
меняется по закону синуса.
Рассмотрим инерционные потери напора 
. Сначала найдем массу жидкости, находящейся во всасывающей линии длиной 
, и её ускорение:
|
|
|
j.
Согласно второму закону Ньютона найдем силу инерции 
:
j.
Относя силу инерции к площади всасывающей линии и к r g, получим выражение для инерционного напора :
j. (6.69)
Итак, инерционный напор меняется по закону косинуса.
Как известно, при j = 0, sin j = 0, cos j = 1,
при j = p/2, sin j = 1, cos j = 0,
при j = p, sin j = 0, cos j = –1
и т.д.
Расчеты показывают, что
Поэтому анализ уравнения (6.63) проведем при максимальном значении инерционного напора 
, т.е. при j = 0. Тогда будем иметь:
(6.70)
При j = 0 инерционный напор имеет максимальное значение, это положение поршня наиболее опасное с точки зрения закипания жидкости, так как давление в полости насоса имеет минимальное значение 
.
Уравнение (6.70) позволяет решить задачи:
– определение допустимой высоты всасывания при 
;
– определения допустимого числа оборотов вала кривошипа
при 
;
Определим высоту всасывания. Максимальное значение 
определяется при 
:
(6.71)
Допустимое значение 
:
(6.72)
где 
– кавитационный запас.
Допустимая высота всасывания для воды при нормальных условиях не превышает 4,0–5,5 м.
Определим частоту вращения вала кривошипа. Из уравнения (6.70) получим:
(6.73)
Допустимое значение 
должно быть меньше максимального 
.
Разумеется, возможна постановка задач определения предельных значений , 
и других параметров насоса.
Процесс нагнетания.
Запишем уравнение Бернулли для сечений х–х и н–н (рис. 6.29).
(6.74)
Из условия нагнетания обычно определяют максимальное значение давления нагнетания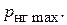 
На это давление рассчитываются детали корпуса насоса. Анализ показывает, что наибольшая величина 
устанавливается в начале хода поршня, т.е. при j = 0. Для этого случая уравнение (6.74) упростится и примет вид:
(6.75)
На рис. 6.30 представлена индикаторная диаграмма поршневого насоса. Линия всасывания 
определяется по формуле (6.63), точка 
– по формуле (6.70); линия нагнетания 
– по формуле (6.74), точка 
–
по формуле (6.75).
Рис. 6.29. Схема линии нагнетания поршневого насоса
Рис. 6.30. Индикаторная диаграмма поршневого насоса
Приведенный анализ относится к насосу простого действия. Этот анализ может быть использован и для насосов двойного действия, только
в последнем случае колебания скоростей воды происходят два раза за один оборот вала.
|
|
|
Наименьшее влияние сил инерции имеет место в насосах тройного действия.
|
|
|
