 |
Процессы сжатия газа в идеальной компрессорной машине
|
|
|
|
В зависимости от условий теплообмена между сжимаемым газом
и окружающей средой теоретически возможны следующие процессы сжатия газа:
– процесс адиабатного сжатия, когда сжатие газа происходит
при отсутствии теплообмена с окружающей средой;
– процесс изотермического сжатия, когда изменение объема
и давления газа протекает при постоянной температуре (T = T 1 = const);
– процесс политропного сжатия газа с частичным отводом тепла
в окружающую среду;
– процесс политропного сжатия газа с частичным подводом тепла извне.
Адиабатный процесс сжатия. Кривая сжатия соответствует уравнению адиабаты:
(7.5)
где 
– показатель адиабаты,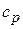 
и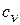 
– теплоемкость газа
при постоянном давлении и при постоянном объеме соответственно.
Будем считать, что приращение кинетической энергии газа
по сравнению с потенциальной незначительно и вторым членом в правой части уравнения (7.4) можно пренебречь. Тогда совместное решение уравнений (7.4) и (7.5) дает:
(7.6)
Используя уравнение состояния газа для начальных условий 
, выражение (7.6) можно представить в виде:
(7.7)
Из выражения (7.7) видно, что удельная работа адиабатного сжатия данного газа зависит лишь от его начальной температуры 
и степени повышения давления e.
Определим температуру в конце сжатия 
. Записав уравнение состояния газа для начала и конца процесса сжатия 
и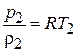 
, получим:
(7.8)
Выразив отношение плотностей из (7.5) как:
и подставив это отношение в (7.8), получим:
(7.9)
Ниже приводятся конечные температуры адиабатического сжатия воздуха для различных e при начальной температуре воздуха 
К (по Цельсию 20 °C). Для воздуха k =1,4.
| e | |||||||||
| T 2, К | |||||||||
| T 2, °C |
Изотермический процесс сжатия газа. Сжатие газа происходит
в соответствии с уравнением изотермы:
|
|
|
(7.10)
Совместное решение уравнений (7.4) и (7.10) дает:
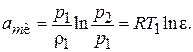(7.11)
Как видно из (7.11), удельная работа изотермического сжатия данного газа зависит от его начальной температуры и степени повышения давления e.
Политропный процесс сжатия газа с частичным отводом тепла. В этом случае кривая сжатия проходит между кривыми адиабатического
и изотермического процессов сжатия газа, следуя уравнению политропы:
(7.12)
Здесь m – показатель политропы, значение которого определяется соотношением:
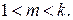
Формулу для определения удельной работы политропного сжатия без учета сообщаемой газу кинетический энергии можно получить совместным решением уравнений (7.4) и (7.12). Тогда получим:
(7.13)
Следует отметить, что значение показателя политропы m будет постоянным в течение всего процесса сжатия лишь в том случае, когда отношение работы сжатия к количеству отводимого тепла всё время остается постоянным. В противном случае его значение будет меняться.
Политропный процесс сжатия с частичным подводом тепла извне. Сжатие происходит по политропе (7.12), но величина показателя политропы m больше, чем показателя адиабаты k.
Удельная работа политропного сжатия с частичным подводом
тепла извне может быть определена по формуле (7.13) с учетом соотношения 
.
Рассмотрим сжатие газа на диаграмме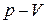 
(рис. 7.2).
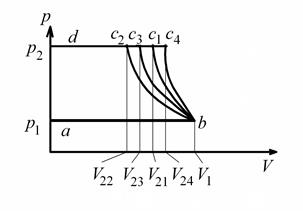
Рис. 7.2. Процессы сжатия газа на диаграмме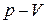
Кривая сжатия газа bc на диаграмме 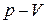может иметь различную крутизну в зависимости от вида процесса сжатия газа.
С ростом интенсивности отвода тепла линия сжатия будет отклоняться от адиабаты (кривая bc 1) влево, крайнее положение этой линии – bc 2.
Линия bc 2 соответствует изотерме, следовательно, всё выделяемое тепло отводится, и температура газа остается постоянной. Линия bc 3 – линия политропного процесса сжатия газа с частичным отводом тепла (m < k), линия bc 4 – кривая политропного сжатия газа с частичным подводом тепла извне (m > k).
|
|
|
Легко заметить, что расходуемая на сжатие газа работа имеет минимальное значение при изотермическом сжатии и максимальное –
при сжатии с частичным подводом тепла извне.
С ростом показателя кривой сжатия 
, согласно формуле (7.9), увеличивается температура газа в конце сжатия .
|
|
|
