 |
П Анализ перемножения диаграмм направленности отдельных
|
|
|
|
Излучателей
Для получения остронаправленных диаграмм в диапазоне сантиметровых и миллиметровых волн в ряде случаев применяются антенны, составленные из большого числа различных типов излучателей.
Получение направленного излучения с помощью линейных антенных систем объясняется интерференцией полей, создаваемых отдельными излучателями. Вследствие этого диаграмма направленности всей антенной системы зависит как от типа излучателей, так и от их расположения, от расстояний между ними, от длины волны и соотношения между амплитудами и фазами токов в излучателях. Соответствующим расположением излучателей и возбуждением в них токов определенных амплитуд и фаз можно получить различные диаграммы направленности.
Напряженность электрического поля в дальней зоне для отдельно взятого N – го излучателя может быть, во многих случаях, определяется следующим выражением:
(2.1п)
Поляризация поля излучателя зависит от вида и расположения последнего в пространстве.
Вектор напряженности поля, создаваемого всеми излучателями, будет равен геометрической сумме всех n векторов напряженностей полей, т.е. при суммировании полей в рассматриваемой точке необходимо учитывать ориентацию каждого вектора в пространстве (поляризацию), а также его амплитуду и фазу.
Если рассматриваемая система состоит из излучателей различного типа, произвольно расположенных в пространстве, задача суммирования полей не может быть упрощена и в общем случае решение получается весьма громоздкими.
Однако для системы идентичных излучателей при их одинаковой ориентации в пространстве общее выражение для результирующей напряженности поля несколько упрощается. В этом случае напряженность поля, создаваемого каждым отдельным излучателем системы в удаленной точке пространства, будет, в частности, характеризоваться одинаковой поляризацией. Поэтому амплитуду общей напряженности поля системы можно определить как сумму комплексных амплитуд составляющих
|
|
|
(2.2п)
Для рассматриваемой системы
,
F1 (φ, θ) = F2 (φ, θ) = … = FN (φ, θ).
Кроме того, учитывая, что линейные размеры системы источников ограниченны и малы по сравнению с расстоянием до точки наблюдения, для амплитудного множителя можно принять
r1 ~ r2 ~ … ~ rN = r.
Поэтому выражение (2.2п) можно упростить, вынеся соответствующие множители за знак суммы,
, (2.3п)
где I1 — ток излучателя 1;
B = i 30 k nД I1 /r (2.4п)
Предположим, что все излучатели рассматриваемой системы являются абсолютно ненаправленными, т. е. что множитель F1 (φ, θ) не зависит от φ и θ и может быть принят равным единице. Тогда
(2.5п)
Последнее выражение определяет напряженность поля в любом направлении (расстояние rN зависит от углов φ и θ).
Абсолютное значение этого выражения определяет диаграмму направленности системы из n ненаправленных излучателей, возбуждаемых токами IN.
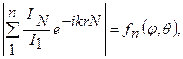(2.6п)
Обозначив выражение, перепишем (2.3п) в виде
E = BF1 (φ, θ) fn (φ, θ). (2.7п)
Множитель B не влияет на форму диаграммы направленности, которая может быть записана в виде
f (φ, θ) = F1 (φ, θ) fn (φ, θ) (2.8п)
Последнее выражение позволяет, сформулировав так называемую теорему перемножения диаграмм направленности, которая гласит:
диаграмма направленности системы из п идентичных и одинаково ориентированных направленных излучателей определяется произведением диаграммы направленности одиночного излучателя на диаграмму направленности той же системы из п воображаемых ненаправленных излучателей.
Выражение (2.8п) имеет очень большое значение в теории антенн, так как оно во многих случаях упрощает исследование вопроса о диаграммах направленности сложных антенных систем. Множитель fN (φ, θ) (2.6п) иногда называют множителем системы или множителем решетки.
|
|
|
|
|
|
