 |
Колебательные процессы. Гармонические колебания и их характеристики: амплитуда, фаза, период и частота.
|
|
|
|
Колебаниями называются движения или процессы, обладающие той или иной повторяемостью во времени.
Гармонические колебания - это такие колебания, при которых колеблющаяся величина x изменяется со временем по закону синуса, либо косинуса: 
, или 
где A - амплитуда;
ω - круговая частота;
α - начальная фаза;
(ωt + α) - фаза.
Фаза колебания - это аргумент гармонической функции: (ωt + α). Начальная фаза α - это значение фазы в начальный момент времени, т.е. при t = 0.
Амплитуда колебания A - это наибольшее значение колеблющейся величины.
При изменении аргумента косинуса, либо синуса на 2π эти функции возвращаются к прежнему значению. Найдем промежуток времени T, в течение которого фаза гармонической функции изменяется на 2π.
ω (t + T) +α = ωt + α + 2π,
или ωT = 2π. 
.
Время T одного полного колебания называется периодом колебания. Частотой называют величину, обратную периоду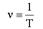 
Единица измерения частоты - герц (Гц), 1 Гц = 1 с-1.
Так как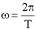 
то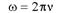 
Круговая, или циклическая частоты ω в 2π раз больше частоты колебаний ν. Круговая частота - это скорость изменения фазы со временем. Действительно: 
.
Метод векторных диаграмм как способ представления гармонических колебаний.
Метод векторных диаграмм.
Гармонические колебания допускают наглядную графическую интерпретацию. Ее смысл состоит в том, что каждому гармоническому колебанию с частотой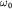 
можно поставить в соответствие вращающийся с угловой скоростью 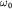вектор, длина которого равна амплитуде 
а его начальное (стартовое) положение задается углом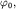 
совпадающим с начальной фазой
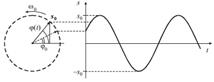
Вертикальная проекция вектора 
изменяется со временем: 
Мгновенное положение вектора определяется углом 
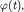который называется фазой и равен: 
|
|
|
При угловой скорости (круговой частоте) 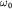вектор совершает 
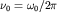оборотов (циклов) в секунду, а продолжительность одного оборота (период) равна отношению угла 
к угловой скорости 
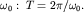
Дифференциальное уравнение гармонических колебаний.
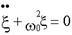, где Кси – колеблющаяся ведичина
Решением дифференциального уравнения называется функция, обращающая это уравнение в тождество. Нетрудно проверить прямой подстановкой, что в нашем случае решение имеет вид: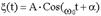 
, т.е. является гармонической функцией. Значит уравнение 
, это дифференциальное уравнение гармонических колебаний.
Пружинный маятник как пример гармонического осциллятора. Собственная частота пружинного маятника.
Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению: F(t) = ma(t) = –mω2x(t).
В этом соотношении ω – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука: Fупр = –kx.
Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими.
Таким образом, груз некоторой массы m, прикрепленный к пружине жесткости k, второй конец которой закреплен неподвижно, составляют систему, способную совершать в отсутствие трения свободные гармонические колебания. Груз на пружине называют линейным гармоническим осциллятором.
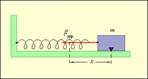
Круговая частота ω0 свободных колебаний груза на пружине находится из второго закона Ньютона: 
откуда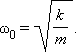 
Частота ω0 называется собственной частотой колебательной системы.
Свободные гармонические колебания в колебательном контуре.
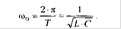
Энергия гармонических колебаний. Превращения энергии в гармоническом осцилляторе (на примере пружинного маятника и колебательного контура)
|
|
|
:1) Пружинный маятник
Мех-е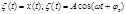 
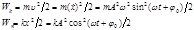
2) Колебательный контур.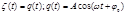 
|
|
|
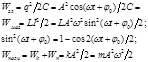
