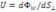Волновое уравнение. Фазовая скорость распространения упругих волн в различных средах.
Рассмотрим волновые уравнения, описывающие различные физические среды. Например, распространение звука в среде описывается уравнением 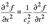 где функция ¦ - описывающая поведение среды (воздуха)
где функция ¦ - описывающая поведение среды (воздуха) 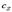 - скорость звукаДалее, если плоская световая волна распространяется вдоль оси x и поляризована так, что электрическое поле E направлено по оси y, то имеем
- скорость звукаДалее, если плоская световая волна распространяется вдоль оси x и поляризована так, что электрическое поле E направлено по оси y, то имеем  где c - скорость света.Уравнение (4.2) является следствием уравнения Максвелла. Уравнения (4.1.), (4.2.) согласно современному представлению теоретической физики, являются уравнением одномерных волн. Для их вывода используется векторная интерпретация точечного вихря. Уравнения содержат временную координату. Эти два условия говорят о том, что в пространстве можно получить решение непосредственно из его физической сущности.Так, решением одномерного волнового уравнения
где c - скорость света.Уравнение (4.2) является следствием уравнения Максвелла. Уравнения (4.1.), (4.2.) согласно современному представлению теоретической физики, являются уравнением одномерных волн. Для их вывода используется векторная интерпретация точечного вихря. Уравнения содержат временную координату. Эти два условия говорят о том, что в пространстве можно получить решение непосредственно из его физической сущности.Так, решением одномерного волнового уравнения 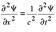 в действительных координатах является функция
в действительных координатах является функция
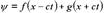 ,где
,где  представляют жесткое перемещение вдоль оси x В пространстве векторная операция точечного вихря определяет функцию
представляют жесткое перемещение вдоль оси x В пространстве векторная операция точечного вихря определяет функцию 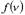 от комплекса
от комплекса 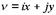 , где
, где 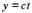 ,как функцию двух действительных функций от двух действительных переменных
,как функцию двух действительных функций от двух действительных переменных  В соответствии с определением производной
В соответствии с определением производной 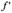 от этой функции по формуле (1.26.) будем иметь
от этой функции по формуле (1.26.) будем иметь 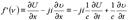 Откуда, приравняв комплексные части получим пространственный ротор. В пространстве
Откуда, приравняв комплексные части получим пространственный ротор. В пространстве 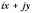 имеем два вектора, имеющих начало в окрестности e -туннеля. Вектора лежатв двух взаимно перпендикулярных плоскостях так, что образуется крутящий момент (рис. 43).Из формулы (4.3) имеем систему уравнений, дающих волновое уравнение.
имеем два вектора, имеющих начало в окрестности e -туннеля. Вектора лежатв двух взаимно перпендикулярных плоскостях так, что образуется крутящий момент (рис. 43).Из формулы (4.3) имеем систему уравнений, дающих волновое уравнение.  .Таким образом, решением волнового уравнения является функция
.Таким образом, решением волнового уравнения является функция 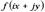 и решение принадлежит четырехмерному пространству, а не плоскости, как считалось до настоящего времени.Комплексные части аналитических функций, определенных в пространстве
и решение принадлежит четырехмерному пространству, а не плоскости, как считалось до настоящего времени.Комплексные части аналитических функций, определенных в пространстве 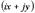 , являются решением волнового уравнения.
, являются решением волнового уравнения.
уравнение вида  , где
, где 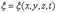 – функция координат и времени,
– функция координат и времени, 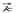 и
и  константы, называется волновым уравнением. колебания частиц среды, длиной волны, фазовой и групповой скоростями, а также законом распределения смещений и напряжений по фронту волны. Особенность У. в. состоит в том, что их фазовая и групповая скорости не зависят от амплитуды и геометрии волны (плоская, сферическая, цилиндрическая волны). Упругие волны, упругие возмущения, распространяющиеся в твёрдой, жидкой и газообразной средах. Например, волны, возникающие в земной коре при землетрясениях, звуковые и ультразвуковые волны в жидкостях и газах и др. При распространении У. в. происходит перенос энергии упругой деформации в отсутствии потока вещества, который имеет место только в особых случаях, например при акустическом ветре. Всякая гармоническая У. в. характеризуется амплитудой и частотой колебания частиц среды, длиной волны, фазовой и групповой скоростями, а также законом распределения смещений и напряжений по фронту волны. Особенность У. в. состоит в том, что их фазовая и групповая скорости не зависят от амплитуды и геометрии волны (плоская, сферическая, цилиндрическая волны). В жидкостях и газах, которые обладают упругостью объёма, но не обладают упругостью формы, могут распространяться лишь продольные волны разрежения — сжатия, где колебания частиц среды происходят в направлении её распространения. Фазовая скорость равна, где К — модуль всестороннего сжатия, r — плотность среды. Пример таких У. в. — звуковые волны (см. Звук).В однородной изотропной бесконечно протяжённой твёрдой среде могут распространяться У. в, только двух типов — продольные и сдвиговые. В продольных движение частиц параллельно направлению распространения волны, а деформация представляет собой комбинацию всестороннего сжатия (растяжения) и чистого сдвига. В сдвиговых волнах движение частиц перпендикулярно направлению распространения волны, а деформация является чистым сдвигом. Фазовая скорость продольных волн, сдвиговых — (G — модуль сдвига). На границе твёрдого полупространства с вакуумом, жидкостью или газом могут распространяться поверхностные Рэлея волны, являющиеся комбинацией неоднородных продольных и сдвиговых волн, амплитуды которых экспоненциально убывают при удалении от границы.
константы, называется волновым уравнением. колебания частиц среды, длиной волны, фазовой и групповой скоростями, а также законом распределения смещений и напряжений по фронту волны. Особенность У. в. состоит в том, что их фазовая и групповая скорости не зависят от амплитуды и геометрии волны (плоская, сферическая, цилиндрическая волны). Упругие волны, упругие возмущения, распространяющиеся в твёрдой, жидкой и газообразной средах. Например, волны, возникающие в земной коре при землетрясениях, звуковые и ультразвуковые волны в жидкостях и газах и др. При распространении У. в. происходит перенос энергии упругой деформации в отсутствии потока вещества, который имеет место только в особых случаях, например при акустическом ветре. Всякая гармоническая У. в. характеризуется амплитудой и частотой колебания частиц среды, длиной волны, фазовой и групповой скоростями, а также законом распределения смещений и напряжений по фронту волны. Особенность У. в. состоит в том, что их фазовая и групповая скорости не зависят от амплитуды и геометрии волны (плоская, сферическая, цилиндрическая волны). В жидкостях и газах, которые обладают упругостью объёма, но не обладают упругостью формы, могут распространяться лишь продольные волны разрежения — сжатия, где колебания частиц среды происходят в направлении её распространения. Фазовая скорость равна, где К — модуль всестороннего сжатия, r — плотность среды. Пример таких У. в. — звуковые волны (см. Звук).В однородной изотропной бесконечно протяжённой твёрдой среде могут распространяться У. в, только двух типов — продольные и сдвиговые. В продольных движение частиц параллельно направлению распространения волны, а деформация представляет собой комбинацию всестороннего сжатия (растяжения) и чистого сдвига. В сдвиговых волнах движение частиц перпендикулярно направлению распространения волны, а деформация является чистым сдвигом. Фазовая скорость продольных волн, сдвиговых — (G — модуль сдвига). На границе твёрдого полупространства с вакуумом, жидкостью или газом могут распространяться поверхностные Рэлея волны, являющиеся комбинацией неоднородных продольных и сдвиговых волн, амплитуды которых экспоненциально убывают при удалении от границы.
Энергия упругих волн. Вектор Умова. Пусть в некой среде распространяется в направлении оси х плоская продольная волна (= a cos ((t - kx + ()Выделим в среде элементарный размер?V, так малый, чтоб скорость движения и деформацию во всех точках этого размера можно было считать одинаковыми и равными, соответственно, и. Выделенный нами размер владеет кинетической энергией(??V – масса размера, – его скорость).Согласно формуле (25.4) 1-го тома рассматриваемый размер владеет также возможной энергией упругой деформации(? = – относительное удлинение цилиндра, Е — модуль Юнга среды).Заменим в согласовании с (5.7) модуль Юнга через?v2 (? – плотность среды, v – фазовая скорость волны). Тогда выражение для возможной энергии размера?V воспримет вид Выражения (6.2) и (6.3) в сумме дают полную энергию Разделив эту энергию на размер?V, в котором она содержится, получим плотность энергии Дифференцирование уравнения (6.1) один раз по t, другой раз по x дает Подставив эти выражения в формулу (6.4) и приняв во внимание, что k2v2 =?2, получим
В случае поперечной волны для плотности энергии выходит такое же выражение.Из (6.5) следует, что плотность энергии в каждый момент времени в различных точках пространства различна. В одной и той же точке плотность энергии меняется со временем по закону квадрата синуса. Среднее значение квадрата синуса равно 1/2. Соответственно среднее по времени значение плотности энергии в каждой точке среды равно Плотность энергии (6.5) и её среднее значение (6.6) пропорциональны плотности среды?, квадрату частоты? и квадрату амплитуды волны а. схожая зависимость имеет место не лишь для незатухающей плоскости волны, но и для остальных видов волн (плоской затухающей, сферической и т. Д.). Итак, среда, в которой распространяется волна, владеет дополнительным запасом энергии. Эта энергия доставляется от источника колебаний в разные точки среды самой волной; следовательно, волна переносит с собой энергию. Количество энергии, переносимое волной через некоторую поверхность в единицу времени, именуется потоком энергии через эту поверхность. Если через данную поверхность переносится за время dt энергия dW, то сгусток энергии? равен сгусток энергии – скалярная величина, размерность которой равна размерности энергии, деленной на размерность времени, т. Е. Совпадает с размерностью мощности. В согласовании с этим? измеряется в ваттах, эрг/с и т. П.сгусток энергии в различных точках среды может быть различной интенсивности. Для свойства течения энергии в различных точках пространства вводится векторная величина, называемая плотностью потока энергии. Эта величина численно равна сгустку энергии через единичную площадку, помещенную в данной точке перпендикулярно к направлению, в котором переносится энергия. Направление вектора плотности потока энергии совпадает с направлением переноса энергии.Пусть через площадку, перпендикулярную к направлению распространения волны, переносится за время?t энергия?W. Тогда плотность потока энергии равна(см. (6.7)). Через площадку (рис. 6.1) Будет перенесена за время?t энергия?W, Тогда плотность потока энергии равна(см. (6.7)). Через площадку (рис. 6.1) Будет перенесена за время?t энергия?W, заключенная в объеме цилиндра с основанием и высотой v?t (v
– фазовая скорость волны). Если размеры цилиндра довольно малы (за счет малости и?t) для того, чтоб плотность энергии во всех точках цилиндра можно было считать одинаковой, то?W можно отыскать как произведение плотности энергии w на размер цилиндра, равный v?t:Подставив это выражение в формулу (6.8), получим для плотности потока энергии:Наконец, введя вектор v, модуль которого равен фазовой скорости волны, а направление совпадает с направлением распространения волны (и переноса энергии), можно написать j = wv Мы получили выражение для вектора плотности потока энергии. Этот вектор был в первый раз введен в рассмотрение выдающимся российским физиком Н. А.
Умовым и именуется вектором Умова. Вектор (6.10), как и плотность энергии w, различен в различных точках про-странства, а в данной точке меняется со временем по закону квадрата синуса. Его среднее значение равно (см. (6.6)). Выражение (6.11), так же как и (6.6), справедливо для волны хоть какого вида (сферической, затухающей и т. Д.).Отметим, что, когда молвят об интенсивности волны в данной точке, то имеют в виду среднее по времени значение плотности потока энергии, переносимой волной.Зная j во всех точках случайной поверхности S, можно вычислить сгусток энергии через эту поверхность. С данной целью разобьем поверхность на элементарные участки dS. За время dt через площадку dS пройдет энергия dW, заключенная в изображенном на рис. 6.2 Косом цилиндре. Размер этого цилиндра равен dV = v dt dS cos?. В нем содержится энергия dW = w dV = w v dtdS cos? (w — мгновенное значение плотности энергии в том месте, где расположена площадка dS). Приняв во внимание, что w v dS cos? = j dS cos? = j dS
(dS = n dS; см. Рис. 6.2), Можно написать: dW = j dS dt. Отсюда для потока энергии d? Через площадку dS выходит формула
(ср. С формулой (11.5)). Полный сгусток энергии через поверхность равен сумме элементарных потоков (6.12):В согласовании с (11.7) можно сказать, что сгусток энергии равен сгустку вектора j через поверхность S.Заменив в формуле (6.13) вектор j его средним по времени значением, получим среднее значение?:Вычислим среднее значение потока энергии через произвольную волновую поверхность незатухающей сферической волны. В каждой точке данной поверхности векторы j и dS совпадают по направлению. Не считая того, модуль вектора j для всех точек поверхности одинаков. Следовательно, (r — радиус волновой поверхности). Согласно (6.11). таковым образом,
(ar – амплитуда волны на расстоянии r от источника). Поскольку энергия волны не поглощается средой, средний сгусток энергии через сферу хоть какого радиуса обязан иметь однообразное значение, т. Е. Обязано выполняться условие
Отсюда следует, что амплитуда а, незатухающей сферической волны обратно пропорциональна расстоянию r от источника волны (см. Формулу (5.10)).
Соответственно средняя плотность потока энергии обратно пропорциональна квадрату расстояния от источника.В случае плоской затухающей волны амплитуда убывает с расстоянием по закону a = = a0 e-?x (см. (2.9)). Соответственно средняя плотность потока энергии (т. Е. Интенсивность волны) убывает по тут (= 2? – величина, называемая коэффициентом поглощения волны. Она имеет размерность, обратную размерности длины. Просто сообразить, что величина, обратная (, равна расстоянию, на котором интенсивность волны миниатюризируется в е раз. УМОВА ВЕКТОР, вектор плотности потока энергии физ. поля; численно равен энергии, переносимой в ед. времени через единичную площадку, перпендикулярную направлению потока энергии в данной точке.
Вектор плотности потока энергии: 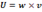 называется Вектором Умова, так как впервые был введен Н.А. Умовым(1874). Вектор направлен в сторону переноса Энергии волной, а по модулю равен отношению потока энергии
называется Вектором Умова, так как впервые был введен Н.А. Умовым(1874). Вектор направлен в сторону переноса Энергии волной, а по модулю равен отношению потока энергии 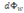 сквозь малую площадку dS к площади
сквозь малую площадку dS к площади  проекции этой площадки на плоскость, перпендикулярную направлению переноса энергии:
проекции этой площадки на плоскость, перпендикулярную направлению переноса энергии:
Воспользуйтесь поиском по сайту:


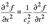 где функция ¦ - описывающая поведение среды (воздуха)
где функция ¦ - описывающая поведение среды (воздуха) 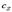 - скорость звукаДалее, если плоская световая волна распространяется вдоль оси x и поляризована так, что электрическое поле E направлено по оси y, то имеем
- скорость звукаДалее, если плоская световая волна распространяется вдоль оси x и поляризована так, что электрическое поле E направлено по оси y, то имеем  где c - скорость света.Уравнение (4.2) является следствием уравнения Максвелла. Уравнения (4.1.), (4.2.) согласно современному представлению теоретической физики, являются уравнением одномерных волн. Для их вывода используется векторная интерпретация точечного вихря. Уравнения содержат временную координату. Эти два условия говорят о том, что в пространстве можно получить решение непосредственно из его физической сущности.Так, решением одномерного волнового уравнения
где c - скорость света.Уравнение (4.2) является следствием уравнения Максвелла. Уравнения (4.1.), (4.2.) согласно современному представлению теоретической физики, являются уравнением одномерных волн. Для их вывода используется векторная интерпретация точечного вихря. Уравнения содержат временную координату. Эти два условия говорят о том, что в пространстве можно получить решение непосредственно из его физической сущности.Так, решением одномерного волнового уравнения 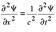 в действительных координатах является функция
в действительных координатах является функция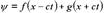 ,где
,где  представляют жесткое перемещение вдоль оси x В пространстве векторная операция точечного вихря определяет функцию
представляют жесткое перемещение вдоль оси x В пространстве векторная операция точечного вихря определяет функцию 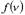 от комплекса
от комплекса 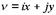 , где
, где 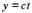 ,как функцию двух действительных функций от двух действительных переменных
,как функцию двух действительных функций от двух действительных переменных  В соответствии с определением производной
В соответствии с определением производной 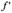 от этой функции по формуле (1.26.) будем иметь
от этой функции по формуле (1.26.) будем иметь 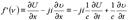 Откуда, приравняв комплексные части получим пространственный ротор. В пространстве
Откуда, приравняв комплексные части получим пространственный ротор. В пространстве 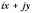 имеем два вектора, имеющих начало в окрестности e -туннеля. Вектора лежатв двух взаимно перпендикулярных плоскостях так, что образуется крутящий момент (рис. 43).Из формулы (4.3) имеем систему уравнений, дающих волновое уравнение.
имеем два вектора, имеющих начало в окрестности e -туннеля. Вектора лежатв двух взаимно перпендикулярных плоскостях так, что образуется крутящий момент (рис. 43).Из формулы (4.3) имеем систему уравнений, дающих волновое уравнение.  .Таким образом, решением волнового уравнения является функция
.Таким образом, решением волнового уравнения является функция 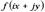 и решение принадлежит четырехмерному пространству, а не плоскости, как считалось до настоящего времени.Комплексные части аналитических функций, определенных в пространстве
и решение принадлежит четырехмерному пространству, а не плоскости, как считалось до настоящего времени.Комплексные части аналитических функций, определенных в пространстве 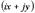 , являются решением волнового уравнения.
, являются решением волнового уравнения. , где
, где 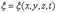 – функция координат и времени,
– функция координат и времени, 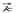 и
и  константы, называется волновым уравнением. колебания частиц среды, длиной волны, фазовой и групповой скоростями, а также законом распределения смещений и напряжений по фронту волны. Особенность У. в. состоит в том, что их фазовая и групповая скорости не зависят от амплитуды и геометрии волны (плоская, сферическая, цилиндрическая волны). Упругие волны, упругие возмущения, распространяющиеся в твёрдой, жидкой и газообразной средах. Например, волны, возникающие в земной коре при землетрясениях, звуковые и ультразвуковые волны в жидкостях и газах и др. При распространении У. в. происходит перенос энергии упругой деформации в отсутствии потока вещества, который имеет место только в особых случаях, например при акустическом ветре. Всякая гармоническая У. в. характеризуется амплитудой и частотой колебания частиц среды, длиной волны, фазовой и групповой скоростями, а также законом распределения смещений и напряжений по фронту волны. Особенность У. в. состоит в том, что их фазовая и групповая скорости не зависят от амплитуды и геометрии волны (плоская, сферическая, цилиндрическая волны). В жидкостях и газах, которые обладают упругостью объёма, но не обладают упругостью формы, могут распространяться лишь продольные волны разрежения — сжатия, где колебания частиц среды происходят в направлении её распространения. Фазовая скорость равна, где К — модуль всестороннего сжатия, r — плотность среды. Пример таких У. в. — звуковые волны (см. Звук).В однородной изотропной бесконечно протяжённой твёрдой среде могут распространяться У. в, только двух типов — продольные и сдвиговые. В продольных движение частиц параллельно направлению распространения волны, а деформация представляет собой комбинацию всестороннего сжатия (растяжения) и чистого сдвига. В сдвиговых волнах движение частиц перпендикулярно направлению распространения волны, а деформация является чистым сдвигом. Фазовая скорость продольных волн, сдвиговых — (G — модуль сдвига). На границе твёрдого полупространства с вакуумом, жидкостью или газом могут распространяться поверхностные Рэлея волны, являющиеся комбинацией неоднородных продольных и сдвиговых волн, амплитуды которых экспоненциально убывают при удалении от границы.
константы, называется волновым уравнением. колебания частиц среды, длиной волны, фазовой и групповой скоростями, а также законом распределения смещений и напряжений по фронту волны. Особенность У. в. состоит в том, что их фазовая и групповая скорости не зависят от амплитуды и геометрии волны (плоская, сферическая, цилиндрическая волны). Упругие волны, упругие возмущения, распространяющиеся в твёрдой, жидкой и газообразной средах. Например, волны, возникающие в земной коре при землетрясениях, звуковые и ультразвуковые волны в жидкостях и газах и др. При распространении У. в. происходит перенос энергии упругой деформации в отсутствии потока вещества, который имеет место только в особых случаях, например при акустическом ветре. Всякая гармоническая У. в. характеризуется амплитудой и частотой колебания частиц среды, длиной волны, фазовой и групповой скоростями, а также законом распределения смещений и напряжений по фронту волны. Особенность У. в. состоит в том, что их фазовая и групповая скорости не зависят от амплитуды и геометрии волны (плоская, сферическая, цилиндрическая волны). В жидкостях и газах, которые обладают упругостью объёма, но не обладают упругостью формы, могут распространяться лишь продольные волны разрежения — сжатия, где колебания частиц среды происходят в направлении её распространения. Фазовая скорость равна, где К — модуль всестороннего сжатия, r — плотность среды. Пример таких У. в. — звуковые волны (см. Звук).В однородной изотропной бесконечно протяжённой твёрдой среде могут распространяться У. в, только двух типов — продольные и сдвиговые. В продольных движение частиц параллельно направлению распространения волны, а деформация представляет собой комбинацию всестороннего сжатия (растяжения) и чистого сдвига. В сдвиговых волнах движение частиц перпендикулярно направлению распространения волны, а деформация является чистым сдвигом. Фазовая скорость продольных волн, сдвиговых — (G — модуль сдвига). На границе твёрдого полупространства с вакуумом, жидкостью или газом могут распространяться поверхностные Рэлея волны, являющиеся комбинацией неоднородных продольных и сдвиговых волн, амплитуды которых экспоненциально убывают при удалении от границы.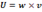 называется Вектором Умова, так как впервые был введен Н.А. Умовым(1874). Вектор направлен в сторону переноса Энергии волной, а по модулю равен отношению потока энергии
называется Вектором Умова, так как впервые был введен Н.А. Умовым(1874). Вектор направлен в сторону переноса Энергии волной, а по модулю равен отношению потока энергии 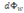 сквозь малую площадку dS к площади
сквозь малую площадку dS к площади  проекции этой площадки на плоскость, перпендикулярную направлению переноса энергии:
проекции этой площадки на плоскость, перпендикулярную направлению переноса энергии: