Волновое уравнение для электромагнитного поля. Электромагнитные волны и их свойства. Энергия электромагнитных волн. Плотность потока электромагнитной энергии - вектор Пойнтинга.

 

Плотность энергии электромагнитного поля равна сумме плотностей для электрического и магнитного полей (при отсутствии сегнетоэлектриков и ферромагнетиков):

.

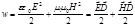Учитывая (2), получим, что 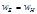для каждого момента времени, тогда

.

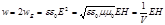
Пойнтинг ввел понятие вектора плотности потока энергии:

 

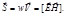
Поток Ф электромагнитной энергии равен

.

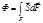
Давление и импульс

Давление электромагнитной волны на тело, на которое она падает возникает в результате воздействия магнитного поля волны на электрические токи, возбуждаемые электрическим полей той же волны.

Пусть электромагнитная волна падает на поглощающее тело (среду), т.е. в нем возникает джоулево тепло с объемной плотностью σЕ², т.е. 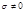и поглощающая среда обладает проводимостью. В такой среде электрическое поле волны возбуждает электрический ток с плотностью . Тогда на единицу объема среды действует амперова сила в направлении волны. Эта сила и вызывает давление электромагнитной волны. Если нет поглощения, σ = 0 и давления нет. При полном отражении волны давление возрастает вдвое.

Давление равно:

Плотность импульса равна 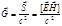, что аналогично выражению 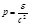для импульса фотона.

Количество энергии излученной волны за некоторый промежуток времени зависит от скорости изменения тока в контуре. При постоянном токе и постоянных зарядах излучение отсутствует. Любой контур, в котором протекает переменный ток, излучает волны. Однако при промышленной частоте f = 50 гц количество энергии излученной волны ничтожно и при расчетах его не принимают во внимание. Излучение незначительно и в диапазоне звуковых частот. Поэтому в радиотехнике используются частоты выше 0,1 Мгц.Не останавливаясь на решении основных уравнений электромагнитного поля в диэлектрике, приведем лишь уравнение Даламбера для векторного потенциала А: 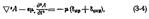где δ _пр = γЕ - плотность тока проводимости; δ _пер = ρM - плотность тока переноса.После преобразования (3-4) получим скалярный потенциал, удовлетворяющий уравнению Даламбера:

При ∂A/∂t = 0 и ∂U/∂t = 0 это уравнение переходит в известное уравнение Пуассона. При ρ = 0, δ _пер = 0 и δ _пр = 0 уравнения (3-4) и (3-5) будут иметь следующий вид:

В таком виде (3-6) и (3-7) носят название волновых уравнений. Электромагнитные возмущения распространяются от центра возмущения с конечной скоростью v, и чем дальше от центра возмущения, тем больше запаздывает их действие: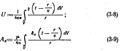

и аналогично для А _у и А _z.Скалярный U и векторный A потенциалы, выражаемые формулами (3-8) и (3-9), называют электродинамическими запаздывающими потенциалами.Электромагнитные волны в изоляции распространяются без затухания, а в металлах они затухают настолько быстро, что даже тонкие слои металла оказываются непроходимыми для волн. Объясняется это тем, что энергия волны переходит по мере ее распространения в металле в тепло. Электромагни́тное излуче́ние (электромагнитные волны) — распространяющееся в пространстве возмущение электромагнитного поля (т.е. иначе говоря - взаимодействующих друг с другом электрического и магнитного полей).Среди электромагнитных полей вообще, порожденных электрическими зарядами и их движением, принято относить собственно к излучению ту часть переменных электромагнитных полей, которая способна распространяться наиболее далеко от своих источников - движущихся зарядов, затухая наиболее медленно с расстоянием.К электромагнитному излучению относятся радиоволны (начиная со сверхдлинных), инфракрасное излучение, видимый свет, ультрафиолетовое, рентгеновское и жесткое (гамма-)излучение (см. ниже, см. также рисунок).Электромагнитное излучение способно распространяться в вакууме (пространстве, свободном от вещества), но в в ряде случаев достаточно хорошо распространяется и в пространстве, заполненном веществом (несколько изменяя при этом свое поведение). Отражение волн. Расположим рупоры генератора и приемника под некоторым углом друг к другу. Приемник отметит отсутствие сигнала. Поместим под рупорами металлическую пластину. Приемник отметит наличие сигнала.Объяснение результатов опыта. Электромагнитная волна, распространяясь в диэлектрической среде (воздухе), отразилась от поверхности проводящей среды (металлической пластины). Преломление волн. Рупоры генератора и приемника расположим напротив друг друга, немного приподняв один из них. При включении генератора приемник отметит отсутствие сигнала. Поместим между рупорами куб из парафина или специальной пластмассы. Приемник отметит наличие сигнала.Объяснение результатов опыта. На границах раздела двух диэлектрических сред (воздуха и парафина) наблюдается преломление электромагнитных волн. Дифракция волн. Расположим рупоры напротив друг друга. При включении генератора приемник отметит наличие сигнала. Поместим вблизи приемного рупора металлический диск. Приемник отметит отсутствие сигнала. Передвинем диск на середину расстояния между рупорами. Приемник отметит наличие сигнала.Объяснение результатов опыта. Если расстояние между диском и приемным рупором мало, волна, хотя и огибает диск, но не попадает в рупор. При отодвигании диска волна, огибая его, смыкается и попадает в приемный рупор. Интерференция волн. Направим излучающий рупор на два металлических листа, расположенные рядом друг с другом под углом, чуть меньшим 180°. Передвигая приемный рупор вокруг листов, мы обнаружим последовательное усиление и ослабление мощности принимаемой волны.

Электрический диполь — система двух равных по модулю разноименных точечных зарядов (+Q,–Q), расстояние l между которыми значительно меньше расстояния до рассматриваемых точек поля. Вектор, направленный по оси диполя (прямой, проходящей через оба заряда) от отрицательного заряда к положи­тельному и равный расстоянию между ними, называется плечом диполя 1. совпадающий по направлению с плечом диполя и равный произведению заряда |Q| на плечо l, называется электрическим моментом диполя или дипольным моментом (рис. 122).

Согласно принципу суперпозиции (80.2), напряженность Е поля диполя в произ­вольной точке

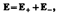
где Е₊ и Е_– — напряженности полей, создаваемых соответственно положительным и отрицательным зарядами. Воспользовавшись этой формулой, рассчитаем напряжен­ность поля в произвольной точке на продолжении оси диполя и на перпендикуляре к середине его оси.

1. Напряженность поля на продолжении оси диполя в точке А (рис. 123). Как видно из рисунка, напряженность поля диполя в точке А направлена по оси диполя и по модулю равна

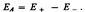
Обозначив расстояние от точки А до середины оси диполя через r, на основании формулы (79.2) для вакуума можно записать

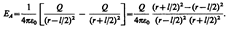
Согласно определению диполя, l/ 2 <<r, поэтому

 

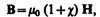(133.7)откуда

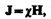(133.6где c — безразмерная величина, называемая магнитной восприимчивостью вещества. Для диамагнстихов c отрицательна (поле молекулярных токов противоположно вне­шнему), для парамагнетиков — положительна (поле молекулярных токов совпадает с

 

⇐ Предыдущая12345

Поделиться:

Воспользуйтесь поиском по сайту: