Волновые процессы и их основные характеристики: длина волны, волновое число. Уравнения плоской и сферической волн.

Под волновым процессом понимают возмущение некоторой величины в пространстве, перемещающееся с конечной скоростью, переносящее мощность без переноса вещества.

Волновой процесс имеет следующие характерные признаки:

1. Волновой процесс всегда переносит энергию и импульсы.

2. Конечная скорость всех волновых процессов.

3. Независимость волновых процессов друг от друга. (В этой комнате существуют поля самых разных частот, поля р/станций, света и т.д.)

4. Волновые процессы, различные по физической природе, описываются одним и тем же математическим аппаратом.

Упругими (механическими) волнами называются механические возмущения, распространяющиеся в упругой среде. Упругие волны бывают продольные и поперечные: в продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных- в плоскостях, перпендикудярных направлению распространения волны.

Длина волны – расстояние между двумя ближайшими точками среды, в которых разность фаз колебаний равна .

Волновое число – число, которое показывает какое количество длин волн укладывается в отрезок .

Длина волны — расстояние между двумя ближайшими друг к другу точками, колеблющимися в одинаковых фазах, обозначается греческой буквой λ. Это одна из основных характеристик колебаний. Измеряется в единицах расстояния (метры, сантиметры и т. п.). Величина , обратная длине волны, называется волновым числом и имеет смысл пространственной частоты.

Получить соотношение, связывающее длину волны с фазовой скоростью (c) и частотой(f) можно из определения. Длина волны соответствует пространственному периоду волны, то есть расстоянию, которое точка с постоянной фазой проходит за время, равное периоду колебаний T, поэтому

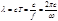
Волнам де Бройля также соответствует определенная длина волны. Частице с энергией Е и импульсом p, соответствуют:

частота: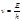

длина волны: ,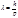

где h — постоянная Планка.

Уравнением волны называется выражение, которое дает сме­щение колеблющейся частицы как функцию ее координат х, у, z и времени t:

x= x(х, у, z, t)

(имеются в виду координаты равновесного положения частицы). Эта функция должна быть периодической как относительно вре­мени t, так и относительно координат х, y, z. Периодичность по времени вытекает из того, что x описывает колебания час­тицы с координатами х, у, z. Периодич­ность по координатам следует из того, что точки, отстоящие друг от друга на расстоя­ние λ, колеблются одинаковым образом.

Волна называется плоской, если ее волновые поверхности представляют совокупность плоскостей, параллельных друг другу. В плоской волне, распространяющейся вдоль оси ОХ, все величины s, характеризующие колебательные движение среды, зависят только от времени и координаты х точки М среды. Колебания происходят по закону s=f(t), но сдвинуты во времени на x\v. Поэтому ур-ие плоской волны имеет вид: s=f(t-x\v). Синусоидальная волна:

s=Asin(wt-wx\v+j0). A=const – амплитуда колебаний (амплит. волны). w=2p\T.

Расстояние l=vT – длина волны. k – волновое число =2p\l=2p\(vT)=w\v.

Волна наз. сферической, если ее волновые поверхности имеют вид концентрическмх сфер. Центр этих сфер наз. центром волны. Ур-ие расходящейся сф. волны: s=j(r)f(t-r\v), где r- расстояние от центра волны до точки М среды. В случае синусоидальной сферической волны: s=A(r)sin(wt-kr+j0), где A(r) – амплитуда волны, j0 – начальная фаза колебаний в центре волны, wt-kr+j0 – фаза сферической волны.

Стоячая волна – волна, образующаяся в результате наложения двух бегущих синусоидальных волн, которые распространяются на встречу друг другу и имеют одинаковые частоты и и амплитуды, а в случае поперечных волн еще и одинаковую поляризацию. Плоская синусоид. стоячая волна имеет вид: s=s1+s2=2Acos(kx+a\2)sin(wt+a\2). Амплитуда стоячей волны

Aст=2A|cos(kx+a\2)|. При Аст=0 точки наз. узлами стоячей волны, а точки в которых Аст максимальна (2А) – пучности стоячей волны. lст=l\2 – длина ст. волны.