 |
Статистические методы оценки качества деталей
|
|
|
|
ДОПУСКИ И ПОСАДКИ ГЛАДКИХ СОЕДИНЕНИЙ
Основные понятия
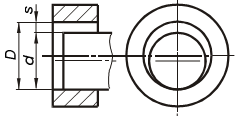
Рассмотрим сопряжение с зазором (рис. 1.1, а). для получения зазора S в сопряжении размер D отверстия втулки должен быть больше размера d вала.
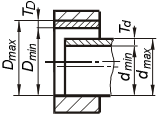
При изготовлении деталей размеры D и d выполняются с погрешностями. Конструктор исходит из того, что погрешности неизбежны, и определяет, в каких пределах они допустимы, т.е. сопряжение еще удовлетворяет требованиям правильной сборки и нормальному функционированию. Конструктор устанавливает два предельных размера для вала - dmax, dmin и два предельных размера для отверстия - Dmax, Dmin, внутри которых должны находиться действительные размеры сопрягаемых деталей (рис. 1.1, б). Разность между наибольшим и наименьшим предельными размерами называется допуском - Td и TD.
| 
| 
|
| а) | б) | в) |
| Рис. 1.1. Сопряжение с зазором
| ||
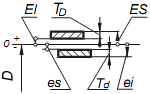
Нанесение на чертеже соединения такого количества размеров крайне не удобно, поэтому было принято устанавливать один общий размер для вала и отверстия, называемый номинальным - D иуказывать от него предельные отклонения (рис. 1.1, в).
Верхнее отклонениеES, es – алгебраическая разность между наибольшим предельным и соответствующим номинальным размерами.
Для отверстия ES = Dmax – D, для вала es = dmax – d.
НижнееотклонениеEI, ei – алгебраическая разность между наименьшим предельным и соответствующим номинальным размерами.
Для отверстия EI = Dmin – D, для вала ei = dmin – d.
Допуск Т – разность между наибольшим и наименьшим предельными размерами или абсолютное значение.
Т = Dmax – Dmin = ½ ES - EI ½ - для отверстий.
Т = dmax – dmin = ½ es - ei ½ - для вала.
Поле допуска – поле, ограниченное наибольшим и наименьшим предельными размерами и определяемое величиной допуска Т и его положением относительно номинального размера.
|
|
|
Графическое изображение полей допусков посадки с зазором приведено на рис. 1.1, в.
Чем уже поле допуска между верхним и нижним отклонением, тем выше при прочих условиях степень точности, которая обозначается цифрой и называется квалитетом.
Основное отклонение – одно из двух отклонений (верхнее или нижнее), ближайшее к нулевой линии и определяющее положение поля допуска относительно нулевой линии. Прописные буквы относятся к отверстиям, а строчные к валам.
Посадка - характер соединения двух деталей, определяемый разностью их размеров до сборки.
Номинальный размер посадки - номинальный размер, общий для отверстия и вала, составляющих соединение.
Посадка характеризует свободу относительного перемещения соединяемых деталей или степень их сопротивления взаимному смещению.
Допуск посадки – сумма допусков отверстия и вала, составляющих соединение.
Зазор (S) – разность размеров отверстия и вала, если размер отверстия больше размера вала.
Натяг (N) – разность размеров вала и отверстия до сборки, если размер вала больше размера отверстия.
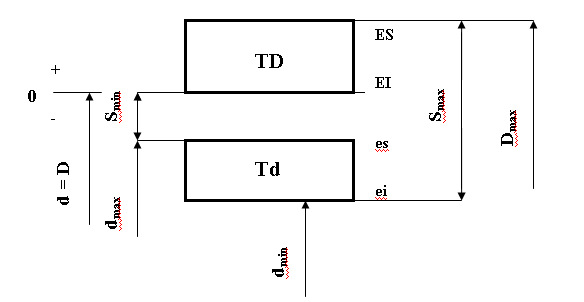
В зависимости от взаимного расположения полей допусков отверстия и вала посадки разделяются на три группы: посадки с зазором; посадки с натягом; переходные посадки (рис. 1.2 - 1.4).
|
| Рис. 1.2. Схема полей допусков посадки с зазором |
|
| Рис. 1.3. Схема полей допусков посадки с натягом |
|
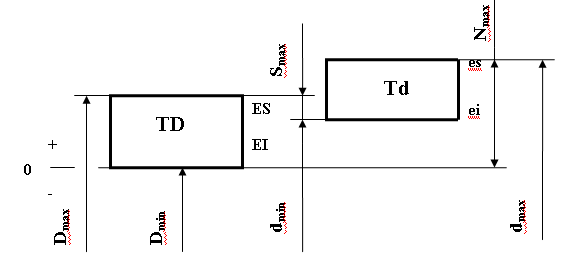
| Рис. 1.4. Схема полей допусков переходной посадки |
Допуски формы и расположения поверхностей.
Шероховатость поверхности
При анализе точности геометрических параметров деталей оперируют следующими понятиями (рис. 1.5).
|
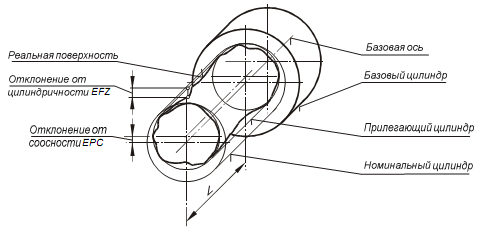
| Рис. 1.5. Геометрические параметры детали |
Номинальная поверхность - идеальная поверхность, размеры и форма которой соответствуют заданным номинальным размерам и номинальной форме.
|
|
|
Реальная поверхность - поверхность, ограничивающая деталь и отделяющая ее от окружающей среды.
Профиль - линия пересечения поверхности с плоскостью или заданной поверхностью (существуют понятия реального и номинального профилей, аналогичные понятиям номинальной и реальной поверхностей).
Нормируемый участок L - участок поверхности или линии, к которому относится допуск формы, допуск расположения или соответствующее отклонение. Если нормируемый участок не задан, то допуск или отклонение относится ко всей рассматриваемой поверхности или длине элемента. Если расположение нормируемого участка не задано, то он может занимать любое расположение в пределах всего элемента.
Прилегающая поверхность - поверхность, имеющая форму номинальной поверхности, соприкасающаяся с реальной поверхностью и расположенная вне материала детали так, чтобы отклонение от нее наиболее удаленной точки реальной поверхности в пределах нормируемого участка имело минимальное значение. Прилегающая поверхность применяется в качестве базовой при определении отклонений формы и расположения.
СТАТИСТИЧЕСКИЕ МЕТОДЫ ОЦЕНКИ КАЧЕСТВА ДЕТАЛЕЙ
Погрешности обработки заготовки распределяются по самым сложным законам, часто довольно сложным – комбинированным.
В среднем можно считать, что при обработке заготовок с повышенной точностью 5–6-го квалитетов и выше, при их обработке по методу пробных проходов, погрешности размеров распределяются по закону равной вероятности.
При обработке заготовок с точностью 7–8-го, а в отдельных случаях и 6-го квалитетов распределение погрешностей подчиняется закону равнобедренного треугольника. При механической обработке заготовок с точностью 8, 9, 10-го квалитетов (и грубее), особенно при автоматическом получении заданных размеров, распределение имеет характер нормального закона.
Приняв гипотезу о предполагаемом распределении погрешностей обработки, надо проверить эту гипотезу. Рекомендуется использовать критерий Пирсона (критерий " χ -квадратов"). Причем можно использовать запись критерия в виде:
,
где noi – опытное число замеров, приходящееся на один i-й интервал; npi – расчетное (соответствующее, предполагаемому закону) число замеров на тот же интервал.
|
|
|
Рекомендуется интервал варьирования разбить на u =5 – 7 элементарным интервалам, для которых подсчитать вероятность попадания переменной. В этом случае число степеней свободы
К = u – 3. Установив число степеней свободы и задавшись уровнем значимости α, по таблице 2.1 установить табличное значение критерия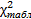 
, если 
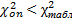гипотеза о предполагаемом законе распределения принимается.
Таблица 2.1
Критические точки распределения χ
| Число степеней свободы К | Уровень значимости α | ||||||
| 0,001 | 0,01 | 0,02 | 0,05 | 0,1 | 0,20 | 0,30 | |
| 2 3 4 5 | 13,82 16,27 18,64 20,5 | 9,21 11,34 13,28 15,09 | 7,82 9,84 11,67 13,39 | 5,99 7,82 9,49 11,07 | 4,6 6,25 7,78 9,24 | 3,22 4,64 5,99 7,29 | 2,41 3,66 4,88 6,06 |
Примечание. Обычно при анализе технологической операции принимается уровень значимости α = 0,05.
При законе равной вероятности попадания случайного значения размера детали в интервале
npi = n / u,
где n – число замерных деталей.
При законе равнобедренного треугольника
npi = nPi,
где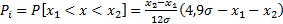 
; σ – стандартное отклонение, найденное по опытным данным; x1 и x2 – размеры границ элементарного интервала.
При нормальном законе распределения np = nPi, где вероятность Pi определяется по таблице 2.2 значений, функций Ф(z) (z= x /σ).
Установив закон распределения случайных погрешностей и подсчитав статистические характеристики распределения, можно установить величину поля рассеяния случайных отклонений размеров заготовки:
- при нормальном распределении ω=6σ;
- при распределении по закону Симпсона ω=4,9σ;
- при распределении по закону равной вероятности ω=3,4σ.
Надежность обработки заготовки без брака характеризуется запасом точности данной операции
ψ=/ω TA,
где TA — поле чертежного допуска детали.
Когда запас точности ψ> 1, обработка заготовки может быть осуществлена без брака (если вероятность брака у анализируемой партии деталей существует, то это указывает на необходимость подналадки cтанка).
При ψ< 1 брак весьма вероятен.
При ψ≥1,2 процесс обработки можно считать надежным.
|
|
|
Таблица 2.2
Табличное значение функции Ф(z)
| z | 0 | 1 | 2 | 3 | 4 |
| 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0 | 0,000 0,0398 0,0793 0,1179 0,1555 0,1915 0,2257 0,2580 0,2881 0,3159 0,3413 0,3643 0,3849 0,4032 0,4192 0,4332 0,4452 0,4554 0,4641 0,4713 0,4772 0,4821 0,4861 0,4893 0,4918 0,4938 0,4953 0,4965 0,4974 0,4981 0,4986 | 0,0040 0,0438 0,0832 0,1217 0,1591 0,1950 0,2291 0,2611 0,2910 0,3183 0,3438 0,3665 0,3869 0,4049 0,4207 0,4345 0,4463 0,4564 0,4649 0,4719 0,4778 0,4826 0,4865 0,4896 0,4920 0,4940 0,4955 0,4966 0,4975 0,4982 0,4987 | 0,0080 0,0478 0,0871 0,1255 0,1628 0,1985 0,2324 0,2642 0,2939 0,3212 0,3461 0,3686 0,3888 0,4066 0,4222 0,4357 0,4474 0,4573 0,4656 0,4726 0,4783 0,4830 0,4868 0,4898 0,4922 0,4941 0,4956 0,4967 0,4976 0,4982 0,4987 | 0,0120 0,0517 0,0909 0,1293 0,1664 0,2019 0,2357 0,2673 0,2967 0,3228 0,3485 0,37 0,3907 0,4082 0,4236 0,4370 0,4484 0,4582 0,4664 0,4732 0,4788 0,4834 0,4871 0,4901 0,4925 0,4943 0,4958 0,4968 0,4977 0,4983 0,4988 | 0,0160 0,0557 0,0948 0,1331 0,1700 0,2045 0,2389 0,2703 0,2995 0,3264 0,3508 0,3729 0,3925 0,4099 0,4251 0,4382 0,4495 0,4591 0,4671 0,4738 0,4793 0,4838 0,4875 0,4904 0,4927 0,4945 0,4959 0,4969 0,4978 0,4984 0,4988 |
Окончание таблицы 2.2
| z | 5 | 6 | 7 | 8 | 9 |
| 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0 | 0,0199 0,0596 0,0987 0,1368 0,1736 0,2088 0,2422 0,2734 0,3023 0,3269 0,3531 0,3749 0,3944 0,4115 0,4265 0,4394 0,4505 0,4599 0,4678 0,4744 0,4798 0,4842 0,4878 0,4906 0,4929 0,4946 0,4960 0,4970 0,4979 0,4984 0,4989 | 0,0239 0,0636 0,1026 0,1406 0,1772 0,2123 0,2454 0,2764 0,3051 0,3315 0,3554 0,3770 0,3962 0,4131 0,4279 0,4406 0,4515 0,4608 0,4686 0,4750 0,4803 0,4846 0,4881 0,4909 0,4931 0,4948 0,4961 0,4971 0,4979 0,4984 0,4989 | 0,0279 0,0675 0,1064 0,1443 0,1808 0,2157 0,2486 0,2794 0,3078 0,3340 0,3577 0,3790 0,3980 0,4147 0,4292 0,4418 0,4525 0,4616 0,4693 0,4756 0,4808 0,4850 0,4884 0,4911 0,4932 0,4949 0,4962 0,4972 0,4979 0,4985 0,4989 | 0,0319 0,0714 0,1103 0,1480 0,1844 0,2190 0,2517 0,2823 0,3106 0,3365 0,3599 0,3810 0,3997 0,4162 0,4306 0,4429 0,4535 0,4625 0,4699 0,4761 0,4812 0,4854 0,4887 0,4913 0,4934 0,4951 0,4963 0,4973 0,4980 0,4986 0,499 | 0,0359 0,0753 0,1141 0,1517 0,1879 0,2224 0,2549 0,2852 0,3133 0,3389 0,3621 0,3830 0,4015 0,4177 0,4319 0,4441 0,4545 0,4633 0,4706 0,4767 0,4817 0,4857 0,4890 0,4916 0,4936 0,4952 0,4964 0,4974 0,4981 0,4986 0,499 |
Варианты индивидуальных заданий приведены в табл. 2.3.
Таблица 2.3
Варианты индивидуальных заданий
| Вариант | Операция | Размеры деталей пробы |
| 0 | Чистовая обточка шейки вала Ø30-0,084 | 29,989 29,975 29,963 29,965 29,975 29,995 29,99 29,965 29,975 29,99 29,985 29,955 29,97 29,98 29,975 29,99 29,975 29,965 29,96 29,96 29,965 29,97 29,985 29,98 29,99 |
| 1 | Шлифование шейки вала Ø30-0,033 | 29,992 29,977 29,986 29,962 29,99 29,989 29,973 29,976 29,972 29,985 29,988 29,978 29,984 29,985 29,98 29,981 29,974 29,985 29,982 29,98 29,978 29,976 29,981 29,982 29,981 |
| 2 | Алмазная расточка отверстия Ø100+0,054 | 100,045 100,015 100,015 100,04 100,022 100,02 100,04 100,01 100,005 100,032 100,025 100,012 100,015 100,04 100,03 100,03 100,03 100,02 100,025 100,03 100,012 100,015 100,04 100,022 100,02 |
| 3 | Получистовая обточка шейки вала Ø60-0,09 | 59,9 59,92 59,99 59.975 59,915 59,95 59,96 59,955 59,95 59,925 59,915 59,97 59,975 59,99 59,92 59,925 59,95 59,955 59,97 59,95 59,94 59,95 59,95 59,96 59,94 |
| 4 | Доводка шейки вала Ø85-0,022 | 84,998 84,997 84,99 84,99 84,988 84,998 84,985 84,992 84,996 84,985 84,988 84,98 84,997 84,98 84,988 84,99 84,995 84,992 84,995 84,995 84,982 84,996 84,985 84,98 84,982 |
| 5 | Шлифование шейки вала Ø85-0,056 | 84,998 84,962 84,975 84,98 84,97 84,985 84968 84,982 84,984 84,98 84,99 84,988 84,975 84,97 84,978 84,992 84,985 84,975 84,982 84,978 84,97 84,985 84,98 84,98 84,976 |
| 6 | Черновая обточка шейки вала Ø50-0,25 | 49,925 49,96 49,975 49,995 49,99 49,975 49,95 49,96 49,975 49,95 49,98 49,97 49,95 49,965 49,975 49,95 49,965 49,97 49,965 49,95 49,965 49,96 49,95 49,96 49,98 |
|
|
|
Окончание таблицы 2.3
| Вариант | Операция | Размеры деталей пробы |
| 7 | Доводка отверстия Ø75+0,019 | 75,019 75,015 75,015 75,005 75,01 75,018 75,001 75,002 75,018 75,01 75,002 75,017 75,014 75,007 75,005 75,002 75,01 75,015 75,019 75,009 75,005 75,019 75,006 75,002 75,006 |
| 8 | Черновое растачивание отверстия Ø60+0,19 | 60,05 60,075 60,075 60,15 60,05 60,075 60,03 60,05 60,04 60,01 60,05 60,075 60,06 60,02 60,08 60,05 60,1 60,08 60,05 60,03 60,075 60,08 60,1 60,075 60,1 |
| 9 | Тонкая обточка шейки вала Ø35-0,039 | 34,988 34,986 34,973 34,971 34,967 34,961 34,991 34,981 34,962 34,983 34,977 34,972 34,984 34,974 34,982 34,977 34,972 34,976 34,987 34,982 34,968 34,976 34,977 34,978 34,978 |
| 10 | Хонингование отверстия Ø200+0.072 | 200,045 200,03 200,024 200,020 200,035 200,055 200,04 200,03 200,02 200,00 200,015 200,045 200,03 200,015 200,010 200,045 200,035 200,03 200,04 200,035 200,03 200.024 200,03 200,03 200,02 |
| 11 | Чистовое шлифование отверстия Ø120+0,09 | 120,085 120,04 120,04 120,02 120,015 120,06 120,05 120,03 120,005 120,075 120,08 120,06 120,05 120,05 120,05 120,065 120,03 120,075 120,06 120,04 120,05 120,05 120,075 120,065 120,065 |
| 12 | Шлифование шейки вала Ø55-0,048 | 54,97 54,98 54,982 54,975 54,988 55,00 54,996 54,98 54,985 54,99 54,978 54,985 54,995 54,978 54,988 54,975 54,982 54,995 54,99 54,99 54,985 54,985 54,982 54,08 54,975 |
| 13 | Чистовое шлифование шейки вала Ø40-0,025 | 39,983 39,982 39,99 39,992 39,982 39,975 39,992 39,986 39,98 39,986 39,994 39,983 39,988 39,997 39,98 39,981 39,99 39,985 39,989 39,99 39,995 39,988 39,986 39,985 39,984 |
Окончание таблицы 2.3
| Вариант | Операция | Размеры деталей пробы |
| 14 | Черновая расточка отверстия Ø65+0,3 | 65,08 65,04 65,06 65,06 65,04 65,04 65,075 65,05 65,05 65,01 65,03 65,03 65,075 65,06 65,02 65,08 65,075 65,02 65,04 65,05 65,075 65,075 65,06 65,06 65,05 |
| 15 | Шлифование шейки вала Ø25-0,084 | 24,925 24,96 24,945 24,95 24,965 24,92 24,985 24,97 24,95 24,925 24,916 24,95 24,985 24,965 24,95 24,935 24,965 24,955 24,95 24,97 24,955 24,95 24,935 24,93 24,94 |
| 16 | Чистовая обточка шейки вала Ø18-0,07 | 17,98 17,99. 17,97 17,97 17,995 17,97 17,985 17,99 17,96 17,965 17,975 17,96 17,985 17,955 17,97 17,975 17,975 17,96 17,965 17,985 17,975 17,97 17,965 17,975 17,98 |
| 17 | Черновая обточка шейки вала Ø55-0,3 | 54,9 54,87 54,85 54,92 54,87 54,95 54,984 54,87 54,9 54,95 54,85 54,8 54,99 54,955 54,9 54,75 54,989 54,87 54,9 54,9 54,92 54,925 54,9 54,955 54,925 |
| 18 | Доводка отверстия Ø50+0,016 | 50,014 50,012 50,005 50,00 50,002 50,01 50,005 50,002 50,01 50,015 50,01 50,014 50,002 50,008 50,002 50,005 50,015 50,005 50,008 50,01 50,005 50,008 50,01 50,002 50,008 |
| 19 | Черновая обточка шейки вала Ø32-0,25 | 31,86 31,9 31.92 31,92 31,99 31,96 31,825 31,9 31,88 31,98 31,92 31,86 31,87 31,94 31,96 31,92 31,9 31,94 31,87 31,88 31,95 31,9 31,92 31,95 31,92 |
| 20 | Шлифование отверстия Ø35+0,089 | 35,022 35,01 35,015 35,018 35,015 35,003 35,004 35,015 35,02 35,025 35,018 35,015 35,005 35,02 35,022 35,012 35,01 35,005 35,015 35,01 35,024 35,018 35,016 35,016 35,012 |
Окончание таблицы 2.3
| Вариант | Операция | Размеры деталей пробы |
| 21 | Черновая обточка шейки вала Ø40-0,16 | 39,99 39,93 39,93 39,97 39,93 39,95 39,965 39,97 39,975 39,93 39,95 39,965 39,96 39,96 39,985 39,95 39,9 39,975 39,95 39,92 39,94 39,95 39,95 39,92 39,95 |
| 22 | Тонкое шлифование шейки вала Ø12-0,011 | 11,989 12,00 11,99 11,997 11,992 11,998 12,00 11,992 11,995 12,00 11.992 11,989 11,995 11,998 12,00 11,997 11,99 11,99 11,989 11,995 11,998 11,995 11,992 11,989 11,995 |
| 23 | Чистовая расточка отверстия Ø125+0,063 | 125,05 125,04 125,04 125,035 125,02 125,02 125,005 125,045 125,025 125,015 125,01 125,024 125,025 125,035 125,03 125,015 125,02 125,03 125,025 125,03 175,035 125,045 125,045 125,03 125,02 |
| 24 | Тонкое шлифование шейки вала Ø20-0,013 | 19,99 19,995 19,997 20,00 19,99 19,99 19,998 19,997 19,989 20,00 19,998 19,992 19,992 19,99 19,995 19,995 19,989 19,99 19,992 19,992 19,995 19,992 19,995 19,942 19,942 |
| 25 | Чистовая расточка отверстия Ø150+0,063 | 150,03 150,025 150,035 150,04 150,025 150,025 150,02 150,008 150,01 150,035 150,025 150,015 150,02 150,04 150,012 150,05 150,04 150,015 150,025 150,03 150,015 150,025 150,025 150,03 150,012 |
Задача 2.1
(Вариант 0 —таблица 2.3)
Для представленной пробы из 25 деталей, обработанных при заданной операции, вычислить числовые характеристики случайных размеров деталей, выдвинуть и проверить рабочую гипотезу о предполагаемом законе распределения случайных размеров, установить точность выполнения анализируемой операции механической обработки, установить возможный процент брака деталей при их обработке без подналадки станка.
Решение
Анализируется операция чистовой обточки вала Ø30-0,084, на основании результатов замера деталей пробы подсчитываются отклонения χ от номинала в мкм: 5, 10, 10, 10, 10, 15, 15, 15, 20, 20, 25, 25, 25, 25, 25, 30, 30, 35, 35, 35, 35, 35, 40, 40, 45 мкм.
Вычисляется среднее арифметическое значение отклонения x =24,6 мкм, стандартное отклонение σ =11,2657 мкм. Так как обрабатывается заготовка с точностью 10 квалитета, выдвигается и проверяется гипотеза о нормальном распределении.
Отклонения размеров деталей от номинала лежат в пределах от 5 до 45 мкм. Интервал варьирования разбивается на 6 равных интервалов протяженностью 8 мкм каждый. Границы интервалов располагаются так, чтобы среднее арифметическое значение лежало вблизи границ 3-го и 4-го интервалов.
Составляется расчетная таблица 2.4.
Таблица 2.4
Расчетная таблица
| Расчетные величины | Номер интервала | ∑ | |||||||||||
| I | II | III | IV | V | VI | ||||||||
| XI-1-XI, мкм | 1 | 9 | 9 | 17 | 17 | 25 | 25 | 33 | 33 | 41 | 41 | 49 | |
| noi | 1 | 7 | 4,5 | 4,5 | 7 | 1 | 25 | ||||||
| xi-1-xi, мкм | -24 | -16 | -16 | -8 | -8 | 0 | 0 | 8 | 8 | 16 | 16 | 24 | - |
| zi-1-zi | -2,13 | -1,42 | -1,42 | -0,71 | -0,71 | 0 | 0 | 0,71 | 0,71 | 1,42 | 1,42 | 2,13 | - |
| Pi | 0.0612 | 0.1611 | 0.2611 | 0.2611 | 0.1611 | 0.0612 | 0.9668 | ||||||
| nPi | 1,53 | 4,04 | 6,53 | 6,53 | 4,04 | 1,53 | 24,2 | ||||||
| n2o i/ nPi | 0,654 | 12,129 | 3,101 | 3,101 | 12,129 | 0,654 | 31,768 | ||||||
Для каждого интервала устанавливается опытная частота: число замеров деталей, приходящихся на интервал (при совпадении размера с границей интервала в два соседних интервала вписывается по 0,5 детали). Размер 25 мкм совпадает с границей интервала, поэтому в III и IV интервалы добавляется по 2,5 единицы.
zi = xi / σ; -2,13; 1, 42; 0,71; 0,71;1, 42;2,13
Вероятность попадания размера в интервал (по таблице 1.2)
PI=PVI =0,4834 - 0,4222 = 0,0612;
PII=PV =0,4222 - 0,2611 = 0,1611;
PIII=PIV =0,2611 – 0 = 0,2611.
Расчетное число деталей в интервале
nPI = nPVI =25 · 0612 = 1,53;
nPII = nPV = 25 · 0,1611= 4,04;
nPIII = nPIV = 25 · 0,2611 = 6,53;
χ2ор = 31,768 – 2 · 25 + 24, 2 = 5,968.
При уровне значимости α=0,05 χ2табл= 7,82 (таблица 1.1) 5,968<7,82 гипотеза о нормальном распределении принимается.
Расчетное поле рассеяния случайных размеров ω=6σ; ω=6 · 11,2657=69,9≈70 мкм.
Точность операции ψ = 84/70 = 1,2 вполне удовлетворительная.
Вероятные предельные размеры:
Наибольший: d max = 30 - 0,0246 + 3 · 0,0112657 = 30,0093 ≈ ≈ 30,009 мм.
Наименьший: d min = 30 - 0,0246 - 3 · 0,0112657 = 29,9416 ≈ 29,942 мм.
Допустимые предельные размеры: Наибольший: d max = 30,0 мм. Наименьший: d min = 30 - 0,084 = 29,916 мм.
Возможен исправимый брак в пределах от 30,0 до 30,009 мм. Вероятность появления этого брака подсчитывается следующим образом.
Определяются отклонения предельных размеров от среднего арифметического значения (x i) в долях σ, т. е. zi = xi / σ i Для размера 30,0 мм (в интервале 0 – x1) значение x1 = 24,6 мкм (т. е. соответствует координате центра группирования или среднеарифметическому значению). Тогда, для интервала «0– z1», z 1 = 24,6 / 11,2657 = 2,18.
Вероятность размеров в интервале 0 – z1 (по таблице 1.2): P1 = 0,4854. Для размера 30,009 (в интервале 0 – x2) значение x 2 = 24,6 + 9 = 33,6 мкм. Тогда z2 = 33,6 / 11,2657 = 3. Вероятность размеров в интервале 0 – z2 (по таблице 1.2): P2 = 0,4986.
Вероятность исправимого брака P брака =0,4986-0,4854=0,013, т. е. 1,3 %.
|
|
|
