Т. е. равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю.

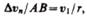Найдем вторую составляющую ускорения. Допустим, что точка В достаточно близка к точке А, поэтому можно считать дугой окружности некоторого радиуса r, мало отличающейся от хорды АВ. Тогда из подобия треугольников АОВ и EAD следует но так как то

 

В пределе при получим

 

Рис.4

Поскольку угол EAD стремится к нулю, а так как треугольник EAD равнобед-

ренный, то угол ADE между стремится к прямому. Следовательно, при

векторы оказываются взаимно перпендикулярными. Так как вектор скорости

направлен по касательной к траектории, то вектор перпендикулярный вектору

Скорости, направлен к центру ее кривизны. Вторая составляющая ускорения, равная

Называется нормальной составляющей ускорения и направлена по нормали к траектории к центру ее кривизны (поэтому ее называют также центростремительным ускорением).

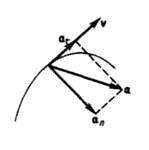
Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих (рис. 5):

Итак, тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории), а нормальная состав­ляющая ускорения — быстроту изменения скорости по направлению (направлена к цен­тру кривизны траектории).

В зависимости от тангенциальной и нормальной составляющих ускорения движе­ние можно классифицировать следующим образом:

1) — прямолинейное равномерное движение;

2) прямолинейное равнопеременное движение. При таком виде движения

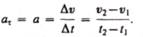
Если начальный момент времени , а начальная скорость то, обозначив

и получим откуда

Проинтегрировав эту формулу в пределах от нуля до произвольного момента времени t, найдем, что длина пути, пройденного точкой, в случае равнопеременного движения

 

Рис. 5

 

3) — прямолинейное движение с переменным ускорением;

4) При скорость по модулю не изменяется, а изменяется по направлению. Из формулы 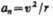следует, что радиус кривизны должен быть посто­янным. Следовательно, движение по окружности является равномерным;

5) — равномерное криволинейное движение;

6) 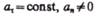— криволинейное равнопеременное движение;

7) — криволинейное движение с переменным ускорением.

Угловая скорость и угловое ускорение

Рассмотрим твердое тело, которое вращается вокруг неподвижной оси. Тогда отдель­ные точки этого тела будут описывать окружности разных радиусов, центры которых лежат на оси вращения. Пусть некоторая точка движется по окружности радиуса R (рис. 6). Ее положение через промежуток времени 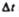зададим углом Элементар­ные (бесконечно малые) повороты можно рассматривать как векторы (они обозначают­ся или Модуль вектора равен углу поворота, а его направление совпадает с направлением поступательного движения острия винта, головка которого вращается в направлении движения точки по окружности, т. е. подчиняется правилу правого винта (рис. 6). Векторы, направления которых связываются с направлением вращения, назы­ваются псевдовекторами или аксиальными векторами. Эти векторы не имеют опреде­ленных точек приложения: они могут откладываться из любой точки оси вращения.

Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:

Вектор направлен вдоль оси вращения по правилу правого винта, т. е. так же, как и вектор (рис. 7). Размерность угловой скорости , а ее е диница — ради-

Ан в секунду (рад/с).

Линейная скорость точки (см. рис. 6)

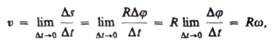
Т. е.

 

В векторном виде формулу для линейной скорости можно написать как векторное произведение:

При этом модуль векторного произведения, по определению, равен

а направление совпадает с направлением поступательного движения правого винта при

его вращения от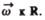

Если то вращение равномерное и его можно характеризовать периодом

вращения Т — временем, за которое точка совершает один полный оборот, т. с. поворачивается на угол Так как промежутку времени соответствует

то откуда

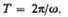
Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения:

откуда

Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:

При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор сонаправлен вектору (рис. 8), при замедлен­ном — противонаправлен ему (рис. 9).

Тангенциальная составляющая ускорения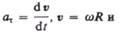

Нормальная составляющая ускорения

Таким образом, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость 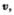тангенциальное ускорение нормальное ускорение и угловыми величинами (угол поворота угловая скорость угловое ускорение выражается следующими формулами:

В случае равнопеременного движения точки по окружности

где — начальная угловая скорость.

Глава 2

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: