Т. е. получили результат, совпадающий с формулой (43.8).

§ 45. Барометрическая формула. Распределение Больцмана

При выводе основного уравнения молекулярно-кинетической теории газов и максвел-ловского распределения молекул по скоростям предполагалось, что на молекулы газа внешние силы не действуют, поэтому молекулы равномерно распределены по объему. Однако молекулы любого газа находятся в потенциальном поле тяготения Земли. Тяготение, с одной стороны, и тепловое движение молекул — с другой, приводят к некоторому стационарному состоянию газа, при котором давление газа с высотой убывает.

Выведем закон изменения давления с высотой, предполагая, что поле тяготения однородно, температура постоянна и масса всех молекул одинакова. Если атмосферное давление на высоте h равно р (рис. 67), то на высоте h + dh оно равно p+dp (при dh>0 так как давление с высотой убывает). Разность давлений р и р+dр равна весу газа, заключенного в объеме цилиндра высотой dh с основанием площадью 1 м²:

p-(p+dp)=pgdh,

где р — плотность газа на высоте h (dh настолько мало, что при изменении высоты в этом пределе плотность газа можно считать постоянной). Следовательно,

dp= -Pgdh. (45.1)

Воспользовавшись уравнением состояния идеального газа 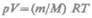(т — масса газа, М — молярная масса газа), находим, что

Подставив это выражение в (45.1), получим

или С изменением высоты от h₁ до h₂ давление изменяется от (рис. 67), т. е.

или

(45.2)

Выражение (45.2) называется барометрической формулой. Она позволяет найти атмос­ферное давление в зависимости от высоты или, измерив давление, найти высоту. Так как высоты обозначаются относительно уровня моря, где давление считается нормаль­ным, то выражение (45.2) может быть записано в виде

(45.3)'

где р — давление на высоте А.

Прибор для определения высоты над земной поверхностью называется высотоме­ром (или альтиметром). Его работа основана на использовании формулы (45.3). Из этой формулы следует, что давление с высотой убывает тем быстрее, чем тяжелее газ.

Барометрическую формулу (45.3) можно преобразовать, если воспользоваться вы­ражением (42.6)

где п — концентрация молекул на высоте h, —то же, на высоте h = 0. Так как — постоянная Авогадро, — масса одной молекулы), а то

(45.4) где m₀gh=П — потенциальная энергия молекулы в поле тяготения, т. е.

(45.5)

Выражение (45.5) называется распределением Больцмана для внешнего потенциаль­ного поля. Из него следует, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул.

Если частицы имеют одинаковую массу и находятся в состоянии хаотического теплового движения, то распределение Больцмана (45.5) справедливо в любом вне­шнем потенциальном поле, а не только в поле сил тяжести.

§ 46. Среднее число столкновений и средняя длина свободного пробега молекул

Молекулы газа, находясь в состоянии хаотического движения, непрерывно сталкивают­ся друг с другом. Между двумя последовательными столкновениями молекулы прохо­дят некоторый путь который называется длиной свободного пробега. В общем случае длина пути между последовательными столкновениями различна, но так как мы имеем дело с огромным числом молекул и они находятся в беспорядочном движении, то можно говорить о средней длине свободного пробега молекул

Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы d (рис. 68). Он зависит от скорости сталкивающихся молекул, т. е. от температуры газа (несколько уменьшается с ростом температуры).

Так как за 1 с молекула проходит в среднем путь, равный средней арифметической скорости , и если — среднее число столкновений, испытываемых одной молеку­лой газа за 1 с, то средняя длина свободного пробега

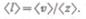
Для определения представим себе молекулу в виде шарика. диаметром d, которая движется среди других «застывших» молекул. Эта молекула столкнется только с теми молекулами, центры которых находятся на расстояниях, равных или меньших d, т. е. лежат внутри «ломаного» цилиндра радиусом d (рис. 69).

Среднее число столкновений за 1 с равно числу молекул в объеме «ломаного» цилиндра:

 

где n — концентрация молекул, — средняя скорость молекулы или

⇐ Предыдущая20212223242526272829Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: