Равна плотности теплового потока при градиенте температуры, равном единице. Можно показать, что

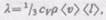(482)

где — удельная теплоемкость газа при постоянном объеме (количество теплоты, необходимое для нагревания 1 кг газа на 1 К при постоянном объеме), — плотность газа, — средняя скорость теплового движения молекул, — средняя длина сво­бодного пробега.

2. Диффузия. Явление диффузии заключается в том, что происходит самопроиз­
вольное проникновение и перемешивание частиц двух соприкасающихся газов, жид­
костей и даже твердых тел; диффузия сводится к обмену масс частиц этих тел,
возникает и продолжается, пока существует градиент плотности. Во время становления
молекулярно-кинетической теории по вопросу диффузии возникли противоречия. Так
как молекулы движутся с огромными скоростями, диффузия должна происходить
очень быстро. Если же открыть в комнате сосуд с пахучим веществом, то запах
распространяется довольно медленно. Однако противоречия здесь нет. Молекулы при
атмосферном давлении обладают малой длиной свободного пробега и, сталкиваясь
с другими молекулами, в основном «стоят» на месте.

Явление диффузии для химически однородного газа подчиняется закону Фика:

(48.3)

где — плотность потока массы — величина, определяемая массой вещества, диффун­дирующего в единицу времени через единичную площадку, перпендикулярную оси х, D — диффузия (коэффициент диффузии), — градиент плотности, равный скоро-

сти изменения плотности на единицу длины х в направлении нормали к этой площадке. Знак минус показывает, что перенос массы происходит в направлении убывания плотности (поэтому знаки противоположны). Диффузия D численно равна

плотности потока массы при градиенте плотности, равном единице. Согласно кинети­ческой теории газов,

(48.4)

3. Внутреннее трение (вязкость). Механизм возникновения внутреннего трения меж­ду параллельными слоями газа (жидкости), движущимися с различными скоростями, заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, движущегося медленнее — увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее.

Согласно формуле (31.1), сила внутреннего трения между двумя слоями газа (жидкости) подчиняется закону Ньютона:

(48.5)

где — динамическая вязкость (вязкость), — градиент скорости, показывающий

быстроту изменения скорости в направлении х, перпендикулярном направлению дви­жения слоев, S — площадь, на которую действует сила F.

Взаимодействие двух слоев согласно второму закону Ньютона можно рассматри­вать как процесс, при котором от одного слоя к другому в единицу времени передается импульс, по модулю равный действующей силе. Тогда выражение (48.5) можно пред­ставить в виде

(48.6)

где — плотность потока импульса — величина, определяемая полным импульсом, переносимым в единицу времени в положительном направлении оси х через единичную

площадку, перпендикулярную оси х, — градиент скорости. Знак минус указывает,

что импульс переносится в направлении убывания скорости (поэтому знаки

противоположны).

Динамическая вязкость численно равна плотности потока импульса при градиенте скорости, равном единице; она вычисляется по формуле

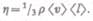(48.7)

Из сопоставления формул (48.1), (48.3) и (48.6), описывающих явления переноса, следует, что закономерности всех явлений переноса сходны между собой. Эти законы были установлены задолго до того, как они были обоснованы и выведены из молекуля-рно-кинетической теории, позволившей установить, что внешнее сходство их математи­ческих выражений обусловлено общностью лежащего в основе явлений теплопровод­ности, диффузии и внутреннего трения молекулярного механизма перемешивания молекул в процессе их хаотического движения и столкновений друг с другом.

Рассмотренные законы Фурье, Фика и Ньютона не вскрывают молекулярно-кинети-ческого смысла коэффициентов Выражения для коэффициентов переноса

выводятся из кинетической теории. Они записаны без вывода, так как строгое рассмот­рение явлений переноса довольно громоздко, а качественное — не имеет смысла. Формулы (48.2), (48.4) и (48.7) связывают коэффициенты переноса и характеристики теплового движения молекул. Из этих формул вытекают простые зависимости между