Таким образом, длина стержня, измеренная в системе, относительно которой он

движется, оказывается меньше длины, измеренной в системе, относительно которой! стержень покоится. Если стержень покоится в системе К, то, определяя его длину) в системе 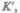опять-таки придем к выражению (37.4).

Из выражения (37.4) следует, что линейный размер тела, движущегося отно­сительно инерциальной системы отсчета, уменьшается в направлении движения в раз, т. е. так называемое лоренцево сокращение длины тем больше, чем

больше скорость движения. Из второго и третьего уравнений преобразований Лоренца I (36.3) следует, что

т. е. поперечные размеры тела не зависят от скорости его движения и одинаковы во всех I инерциальных системах отсчета. Таким образом, линейные размеры тела наибольшие I в той инерциальной системе отсчета, относительно которой тело покоится.

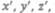4. Релятивитский закон сложения скоростей. Рассмотрим движение материальной I точки в системе в свою очередь движущейся относительно системы К со скоро- стью v. Определим скорость этой же точки в системе К. Если в системе К движение точки в каждый момент времени t определяется координатами х, у, z, а в системе в момент времени — координатами то

представляют собой соответственно проекции на оси вектора скорости

рассматриваемой точки относительно систем Согласно преобразованиям Лоренца (36.3),

_______

скоростей специальной теории относительности:

(37.5)

Если материальная точка движется параллельно оси х, то скорость и относительно системы К совпадает с а скорость 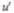относительно Тогда закон сложения

Скоростей примет вид

(37.6)

Легко убедиться в том, что если скорости v, и' и и малы по сравнению со скоростью с, то формулы (37.5) и (37.6) переходят в закон сложения скоростей в классической

Механике (см. (34.4)). Таким образом, законы релятивистской механики в предельном случае для малых скоростей (по сравнению со скоростью распространения света в вакууме) переходят в законы классической физики, которая, следовательно, является частным случаем механики Эйнштейна для малых скоростей.

Релятивистский закон сложения скоростей подчиняется второму постулату Эйнш­тейна (см. § 35). Действительно, если то формула (37.6) примет вид

(аналогично можно показать, что при и=с скорость также равна с). Этот результат свидетельствует о том, что релятивистский закон сложения скоростей находится в со­гласии с постулатами Эйнштейна.

Докажем также, что если складываемые скорости сколь угодно близки к скорости с, то их результирующая скорость всегда меньше или равна с. В качестве примера рассмотрим предельный случай 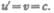После подстановки в формулу (37.6) получим

Таким образом, при сложении любых скоростей результат не может превысить скорости света с в вакууме. Скорость света в вакууме есть предельная скорость, которую невозможно превысить. Скорость света в какой-либо среде, равная с/л (л — абсолютный показатель преломления среды), предельной величиной не является (подробнее см. § 189).

Интервал между событиями

Преобразования Лоренца и следствия из них приводят к выводу об относительности длин и промежутков времени, значение которых в различных системах отсчета разное. В то же время относительный характер длин и промежутков времени в теории Эйнштейна означает относительность отдельных компонентов какой-то реальной фи-зической величины, не зависящей от системы отсчета, т. е. являющейся инвариантной по отношению к преобразованиям координат. В четырехмерном пространстве Эйнш­тейна, в котором каждое событие характеризуется четырьмя координатами (х, у, z, t), такой физической величиной является интервал между двумя событиями:

(38.1)

где — расстояние между точками трехмерного

пространства, в которых эти события произошли. Введя обозначение получим

Покажем, что интервал между двумя событиями одинаков во всех инерциальных системах отсчета. Обозначив 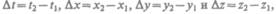выражение

(38.1) можно записать в виде

Интервал между теми же событиями в системе К' равен

(38.2)

⇐ Предыдущая15161718192021222324Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: