 |
Удовлетворяет лишь идеальный газ, и оно является уравнением состояния идеального газа, называемым также уравнением Клапейрона — Менделеева.
|
|
|
|
Числовое значение молярной газовой постоянной определим из формулы (42.4), полагая, что моль газа находится при нормальных условиях (ро= 1,013 105 Па,
Т0=273,15 К, Vm=22,41.10-3 м3/моль): R=8,31 Дж/ДмольК).
От уравнения (42.4) для моля газа можно перейти к уравнению Клапейрона — Менделеева для произвольной массы газа. Если при некоторых заданных давлении и температуре один моль газа занимает молярный объем Vm, то при тех же


|

|
условиях масса т газа займет объем V= (m/M) Vm, где М — молярная масса (масса
одного моля вещества). Единица молярной массы — килограмм на моль (кг/моль). Уравнение Клапейрона — Менделеева для массы т газа
 (42.5)
(42.5)
где  — количество вещества.
— количество вещества.
Часто пользуются несколько иной формой уравнения состояния идеального газа, вводя постоянную Больцмана:

Исходя из этого уравнение состояния (42.4) запишем в виде
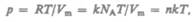
где 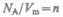 — концентрация молекул (число молекул в единице объема). Таким
— концентрация молекул (число молекул в единице объема). Таким
Образом, из уравнения
 (42.6)
(42.6)
следует, что давление идеального газа при данной температуре прямо пропорционально концентрации его молекул (или плотности газа). При одинаковых температуре и давлении все газы содержат в единице объема одинаковое число молекул. Число молекул, содержащихся в 1 м3 газа при нормальных условиях, называется числом Лошмидта*:

Основное уравнение молекулярно-кинетической теории идеальных газов
Для вывода основного уравнения молекулярно-кинетической теории рассмотрим одно-атомный идеальный газ. Предположим, что молекулы газа движутся хаотически, число взаимных столкновений между молекулами газа пренебрежимо мало по сравнению с числом ударов о стенки сосуда, а соударения молекул со стенками сосуда абсолютно упругие. Выделим на стенке сосуда некоторую элементарную площадку  (рис. 64) и вычислим давление, оказываемое на эту площадку. При каждом соударении молекула, движущаяся перпендикулярно площадке, передает ей импульс
(рис. 64) и вычислим давление, оказываемое на эту площадку. При каждом соударении молекула, движущаяся перпендикулярно площадке, передает ей импульс 
|
|
|
где то — масса молекулы,  — ее скорость. За время
— ее скорость. За время  площадки
площадки  достигнут только
достигнут только
те молекулы, которые заключены в объеме цилиндра с основанием  и высотой
и высотой  (рис. 64). Число этих молекул равно
(рис. 64). Число этих молекул равно  (n — концентрация молекул).
(n — концентрация молекул).
Необходимо, однако, учитывать, что реально молекулы движутся к площадке  под разными углами и имеют различные скорости, причем скорость молекул при каждом соударении меняется. Для упрощения расчетов хаотическое движение молекул заменяют движением вдоль трех взаимно перпендикулярных направлений, так что в любой момент времени вдоль каждого из них движется
под разными углами и имеют различные скорости, причем скорость молекул при каждом соударении меняется. Для упрощения расчетов хаотическое движение молекул заменяют движением вдоль трех взаимно перпендикулярных направлений, так что в любой момент времени вдоль каждого из них движется  молекул, причем половина
молекул, причем половина
молекул  движется вдоль данного направления в одну сторону, половина — в
движется вдоль данного направления в одну сторону, половина — в
противоположную. Тогда число ударов молекул, движущихся в заданном направлении, о площадку 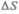 будет
будет  При столкновении с площадкой эти молекулы
При столкновении с площадкой эти молекулы
Передадут ей импульс
 •И. Лошмидт (1821—1895) — австрийский химик и физик.
•И. Лошмидт (1821—1895) — австрийский химик и физик.

Тогда давление газа, оказываемое им на стенку сосуда,
 (43.1)
(43.1)
Если газ в объеме V содержит N молекул, движущихся со скоростями  то
то
Целесообразно рассматривать среднюю квадратичную скорость
 (43,2)
(43,2)
Характеризующую всю совокупность молекул газа. Уравнение (43.1) с учетом (43.2) примет вид
 (43.3)
(43.3)
Выражение (43.3) называется основным уравнением молекулярно-кмнетнческой теории идеальных газов. Точный расчет с учетом движения молекул по всевозможным направлениям дает ту же формулу.
Учитывая, что n—N/V, получим
 (43.4) или
(43.4) или
 (43.5)
(43.5)
где Е — суммарная кинетическая энергия поступательного движения всех молекул газа.
Так как масса газа m = Nm0, то уравнение (43.4) можно переписать в виде
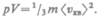
Для одного моля газа т=М(М — молярная масса), поэтому
|
|
|

где Vm — молярный объем. С другой стороны, по уравнению Клапейрона — Менделеева, pVm = RT. Таким образом,


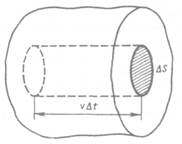
|

|
Откуда
 (43.6)
(43.6)
Так как M=m0NА где mо — масса одной молекулы, а 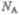 — постоянная Авогадро, то из уравнения (43.6) следует, что
— постоянная Авогадро, то из уравнения (43.6) следует, что
 (43.7)
(43.7)
где k=R/NA — постоянная Больцмана. Отсюда найд ем, что при комнатной температуре молекулы кислорода имеют среднюю квадратичную скорость 480 м/с, водорода — 1900 м/с. При температуре жидкого гелия те же скорости будут соответственно 40 и 160 м/с.
Средняя кинетическая энергия поступательного движения одной молекулы идеального газа
 (43.8)
(43.8)
(использовали формулы (43.5) и (43.7)) пропорциональна термодинамической температуре и зависит только от нее. Из этого уравнения следует, что при 
т. е. при 0 К прекращается поступательное движение молекул газа, а следовательно, его давление равно нулю. Таким образом, термодинамическая температура является мерой средней кинетической энергии поступательного движения молекул идеального газа, и формула (43.8) раскрывает молекулярно-кинетическое толкование температуры.
§ 44. Закон Максвелла о распределении молекул идеального газа по скоростям и энергиям теплового движения
При выводе основного уравнения молекулярно-кинетической теории молекулам задавали различные скорости. В результате многократных соударений скорость каждой молекулы изменяется по модулю и направлению. Однако из-за хаотического движения молекул все направления движения являются равновероятными, т. е. в любом направлении в среднем движется одинаковое число молекул.
По молекулярно-кинетической теории, как бы ни изменялись скорости молекул при столкновениях, средняя квадратичная скорость молекул массой mо в газе, находящемся
в состоянии равновесия при Т= const, остается постоянной и равной 
Это объясняется тем, что в газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону. Этот закон теоретически выведен Дж. Максвеллом.
При выводе закона распределения молекул по скоростям Максвелл предполагал, что газ состоит из очень большого числа N тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Предполагалось также, что силовые поля на газ не действуют.
|
|
|
Закон Максвелла описывается некоторой функцией  называемой функцией
называемой функцией
распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, равные  то на каждый интервал скорости будет приходиться некоторое число молекул
то на каждый интервал скорости будет приходиться некоторое число молекул  имеющих скорость, заключенную в этом интервале.
имеющих скорость, заключенную в этом интервале.
Функция 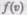 определяет относительное число молекул
определяет относительное число молекул 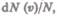 скорости которых
скорости которых
лежат в интервале от 

откуда
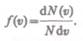
Применяя методы теории вероятностей, Максвелл нашел функцию — закон о распределении молекул идеального газа п о скоростям: 
 (44.1)
(44.1)
Из (44.1) видно, что конкретный вид функции зависит от рода газа (от массы молекулы) и от параметра состояния (от температуры Т).
График функции (44.1) приведен на рис. 65. Так как при возрастании v множитель ехр  уменьшается быстрее, чем растет множитель
уменьшается быстрее, чем растет множитель  , то функция
, то функция 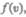
начинаясь от нуля, достигает максимума при  и затем асимптотически стремится к нулю. Кривая несимметрична относительно
и затем асимптотически стремится к нулю. Кривая несимметрична относительно  .
.
Относительное число молекул  скорости которых лежат в интервале от
скорости которых лежат в интервале от
 находится как площадь заштрихованной полоски на рис. 65. Площадь, ограниченная кривой распределения и осью абсцисс, равна единице. Это означает, что функция
находится как площадь заштрихованной полоски на рис. 65. Площадь, ограниченная кривой распределения и осью абсцисс, равна единице. Это означает, что функция 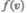 удовлетворяет условию нормировки
удовлетворяет условию нормировки

Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью. Значение наиболее вероятной скорости можно найти продифференцировав выражение (44.1) (постоянные множители опускаем) по аргументу v, приравняв результат нулю и используя условие для максимума  выражения
выражения 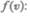
Значения 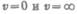 соответствуют минимумам выражения (44.1), а значение v, при
соответствуют минимумам выражения (44.1), а значение v, при
котором выражение в скобках становится равным нулю, и есть искомая наиболее вероятная скорость 
 (44.2) Из формулы (44.2) следует, что при повышении температуры максимум функции
(44.2) Из формулы (44.2) следует, что при повышении температуры максимум функции


|

|
распределения молекул по скоростям (рис. 66) сместится вправо (значение наиболее вероятной скорости становится больше). Однако площадь, ограниченная кривой, остается неизменной, поэтому при повышении температуры кривая распределения молекул по скоростям будет растягиваться и понижаться.
|
|
|
Средняя скорость молекулы 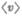 (средни арифметическая скорость) определяется по формуле
(средни арифметическая скорость) определяется по формуле
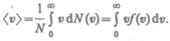
Подставляя сюда  и интегрируя, получаем
и интегрируя, получаем
 (44.3) Скорости, характеризующие состояние газа: 1) наиболее вероятная
(44.3) Скорости, характеризующие состояние газа: 1) наиболее вероятная 
2) средняя  3) средняя квадратичная
3) средняя квадратичная 
(рис. 65). Исходя из распределения молекул по скоростям
 (44.4)
(44.4)
можно найти распределение молекул газа по значениям кинетической энергии Е. Для этого перейдем от переменной v к переменной 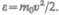 Подставив в (44.4)
Подставив в (44.4) 
и  получим
получим

где  — число молекул, имеющих кинетическую энергию поступательного движе-
— число молекул, имеющих кинетическую энергию поступательного движе-
ния, заключенную в интервале от 
|
|
|


