Правила вычисления определителей.

 

Опр. Определитель 1-го порядка – это определитель квадратной матрицы 1-го порядка А₁, который равен значению элемента а₁₁, так как матрица А₁ состоит из одного этого элемента, который одновременно является ее числовой характеристикой: D=|A₁|= a₁₁.

 

Опр. Определитель 2-го порядка – это определитель квадратной матрицы 2-го порядка А₂, который вычисляется по формуле

D = |A₂| = = a₁₁×a₂₂ - а₁₂×а₂₁, (2.1)

то есть он равен разности произведений элементов главной и побочной диагоналей (рис.2.1).

 

 

Рисунок 2.1

Пример. =1×4 - (-2)×3 = 10

Опр. Определитель 3-го порядка – это определитель квадратной матрицы 3-го порядка А₃, который вычисляется по формуле

D = |A₃| = =

= а₁₁×а₂₂×а₃₃ + а₁₂×а₂₃×а₃₁ + а₁₃×а₂₁×а₃₂ - а₁₃×а₂₂×а₃₁ - а₁₂×а₂₁×а₃₃ - а₁₁×а₂₃×а₃₂ (2.2)

 

Для запоминания формулы (2.2) используют правило треугольников, которое символически изображено на рисунке 2.2.

 

 

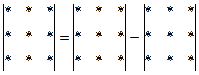
Рисунок 2.2

 

Со знаком (+) берутся произведения элементов, стоящих на главной диагонали, и произведения элементов, стоящих в вершинах треугольников, основания которых параллельны главной диагонали. Со знаком (-) берутся произведения элементов, стоящих на побочной диагонали, и произведения элементов, стоящих в вершинах треугольников, основания которых параллельны побочной диагонали.

 

Пример. D= = 5×1×(-3) + (-2)×(-4)×6 + 3×0×1 - 1×1×6 - (-2)×3×(-3) - (-4)×0×5 = 9

Опр. Минор M_ij элемента a_ij - это определитель, который получается из исходного определителя вычеркиванием i-й строки и j-го столбца, на пересечении которых находится элемент a_ij. Например,

if D= Þ M₁₁ = , то есть М₁₁ = ; М₁₂ = ,…,

М₃₃ =

Опр. Алгебраическое дополнение A_ij элемента a_ij - это минор M_ij, взятый со знаком (-1)^i+j, то есть A_ij = (-1)^i+j×M_ij. Например,

if D= Þ А₁₁=(-1)²× М₁₁ = ; А₁₂=(-1)³× М₁₂ = - ,…, А₃₃=(-1)⁶× М₃₃ = .

Теорема Лапласа (точнее, частный случай теоремы Лапласа).

Всякий определитель равен сумме попарных произведений элементов любой его строки (столбца) на соответствующие алгебраические дополнения, то есть

D = |A_n| = 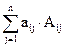= , (2.3)

где 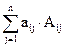есть разложение определителя по i-ой строке, а есть разложение определителя по j-му столбцу.

Доказательство.

Убедимся в справедливости теоремы Лапласа на примере разложения определителя 3-го порядка, например, по 1-й строке. По теореме это разложение будет иметь вид: D= = а₁₁А₁₁ + а₁₂А₁₂ + а₁₃А₁₃ = {с учетом определения A_ij получим}= =а₁₁(-1)²М₁₁ + а₁₂(-1)³М₁₂ + а₁₃(-1)⁴М₁₃ = а₁₁ - а₁₂ + а₁₃ = а₁₁(а₂₂×а₃₃ - а₂₃×а₃₂) - а₁₂(а₂₁×а₃₃ - а₂₃×а₃₁) + а₁₃(а₂₁×а₃₂ - а₂₂×а₃₁) = =а₁₁×а₂₂×а₃₃ + а₁₂×а₂₃×а₃₁ + а₁₃×а₂₁×а₃₂ - а₁₃×а₂₂×а₃₁ - а₁₂×а₂₁×а₃₃ - а₁₁×а₂₃×а₃₂ = {по правилу треугольников} = = D. Аналогичный результат получается при разложении определителя по любой строке (столбцу). Fin.

Следствие. Если в i–й строке (j-м столбце) определителя D есть только один ненулевой элемент а_ij ¹ 0, то результатом разложения определителя по этой строке (столбцу) будет выражение D = а_ij×А_ij.

 

Свойства определителей.

 

1) При транспонировании определителя его значение не меняется, (то есть значение определителя не меняется при замене его строк столбцами с теми же номерами).

Доказательство:

D = = = a₁₁×a₂₂ - а₁₂×а₂₁

NB. Следовательно, строки и столбцы определителя равноправны, поэтому его свойства можно формулировать и доказывать либо для строк, либо для столбцов.

2) При взаимной перестановке любых двух строк (столбцов) определителя его знак меняется на противоположный.

Доказательство:

D = = a₁₁×a₂₂ - а₁₂×а₂₁ = - (а₁₂×а₂₁ - a₁₁×a₂₂) = -

 

3) Определитель с двумя одинаковыми строками (столбцами) равен нулю.

Доказательство. Пусть определитель D имеет две одинаковые строки. Если поменять их местами, то, с одной стороны, величина определителя не изменится, так как строки одинаковы, а с другой стороны определитель должен поменять свой знак на противоположный по свойству 2. Таким образом, имеем: D = -D Þ D = 0.

4) Общий множитель элементов какой-либо строки (столбца) можно выносить за знак определителя.

Доказательство:

D= = la₁₁×a₂₂ - lа₁₂×а₂₁ = l(a₁₁×a₂₂ - а₁₂×а₂₁) = l .

Следствие: D = = l×m .

NB. Правило умножения определителя на число. Чтобы умножить определитель на число, надо все элементы какой-то одной его строки (столбца) умножить на это число.

5) Определитель с нулевой строкой (столбцом) равен нулю.

Доказательство. По свойству 4 вынесем общий множитель l = 0 элементов нулевой строки (столбца) за знак определителя. Получим 0×D = 0.

6) Определитель с двумя и более пропорциональными строками (столбцами) равен нулю.

Доказательство. Если вынести за знак определителя коэффициент пропорциональности двух строк (столбцов) l≠0, то получится определитель с двумя одинаковыми строками (столбцами), равный нулю по свойству 3.

7) Если каждый элемент какой-либо строки (столбца) определителя представить в

виде суммы k слагаемых, то такой определитель равен сумме k определителей, у которых элементы этой строки (столбца) заменены соответствующими слагаемыми, а все остальные элементы такие же как у исходного определителя.

Доказательство:

D= = (а₁₁ + b₁₁)а₂₂ - (а₁₂ + b₁₂)а₂₁ = (а₁₁а₂₂ - а₁₂а₂₁) + (b₁₁а₂₂ - b₁₂а₂₁) = = + .

 

Опр. n-ая строка определителя называется линейной комбинацией его остальных (n-1) строк, если ее можно представить в виде суммы произведений этих строк на соответствующие числа l₁, l₂, …, l_n-1. Например, в определителе

 

3–я строка является линейной комбинацией первых двух строк.

NB. Линейная комбинация называется тривиальной, если в ней "l_i = 0. В противном случае линейная комбинация называется нетривиальной (if $l_i ¹ 0).

8 а) Если одна строка (столбец) определителя является линейной комбинацией других его строк (столбцов), то такой определитель равен нулю.

Доказательство: D =

8 б) Величина определителя не изменится, если к элементам любой его строки (столбца) прибавить соответствующие элементы любой другой строки (столбца) определителя, умноженные на одно и то же число.

Доказательство:

Пусть D= Þ {к 1-й строке прибавим 2-ю строку, умноженную на число l} Þ

Þ = .

9) Сумма произведений элементов какой-либо строки (столбца) определителя на алгебраические дополнения соответствующих элементов любой другой строки (столбца) определителя равна нулю, то есть = 0 (if i ≠ j).Например, пусть

D = ¹ 0

Тогда а₁₁А₂₁ + а₁₂А₂₂ + а₁₃А₂₃ = 0, так как выполнено умножение элементов 1-ой строки определителя на алгебраические дополнения соответствующих элементов 2-ой строки.

Доказательство:

а₁₁А₂₁ + а₁₂А₂₂ + а₁₃А₂₃ = а₁₁×(-1)²⁺¹ 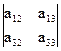+ а₁₂×(-1)²⁺² + а₁₃×(-1)²⁺³ =

={это есть разложение по 1-й строке определителя (-1)× = 0}= 0.

Если определитель D¹0, то по свойству 8 б) в нем всегда можно «обнулить» i-ю строку (j-й столбец) до единственного ненулевого элемента и разложить определитель по этой строке (столбцу). Применяя эту операцию нужное число раз, всегда можно из определителя n-го порядка получить определитель 2-го порядка.

Пример 1. Вычислить определитель D =

Решение: Используя свойство 8 б) определителей, проще всего 2-ую строку «обнулить» до единственного ненулевого элемента, так как ее элементы минимальны по абсолютной величине и она уже содержит один ноль. Для этой цели выберем в определителе так называемый активный столбец, ненулевой элемент которого стоящий на пересечении с обнуляемой строкой должен быть минимальным по модулю из всех элементов этой строки (оптимально, если он равен ±1.). В данном случае таких столбцов два: 1-ый и 3-ий. Возьмем в качестве активного 3-ий столбец, так как у него со 2-ой строкой общий элемент а₂₃=1 и по сравнению с 1-ым столбцом его элементы по модулю меньше. Чтобы обнулить 1-ый элемент 2-ой строки, умножим активный столбец на (-1) и прибавим его к 1-му столбцу. Аналогично, чтобы обнулить 4-ый элемент 2-ой строки, умножим активный столбец на (-2) и прибавим его к 4-му столбцу. В результате, во 2-ой строке останется только один ненулевой элемент а₂₃=1 (который принадлежит активному столбцу). Запишем эти действия:

 

^{-1 -2}

D= = = {разложим определитель по 2-ой строке согласно правилу разложения определителя по элементам строки (столбца)} = а₂₃×А₂₃ = =1×(-1)²⁺³×М₂₃ = - = {вынесем за знак определителя множитель (-2) 1-й строки и для «обнуления» этой строки используем 2-ой столбец в качестве активного}=

_{1 1}

= 2× = 2× = {разложим определитель по 1-ой строке}= =2×(-1)×(-1)¹⁺²× ={вынесем за знак определителя множитель (3) 1-го столбца}= =2×3× = 6×(-3-1) = -24.

Пример 2. Вычислить определитель D =

Решение. D= ={вынесем за знак определителя множитель (2) 1-ой строки}= =2 = 2 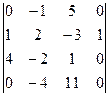= 2×а₂₄×А₂₄ =2×1×(-1)⁶×М₂₄ =2 = =2×4×(-1)³× = 8× = 8×(11-20) = -72

NB 1. В случае если обнуляющий элемент активной строки (столбца) не равен ±1, то, используя линейную комбинацию соответствующих строк (столбцов), всегда можно добиться того, чтобы он стал равен ±1.

Пример 3. Вычислить определитель

Решение. = ^-2 = = 1×(-1)³⁺¹ 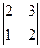= 4-3 = 1

NB 2. Определитель треугольного вида равен произведению его диагональных элементов, то есть = = а₁₁×а₂₂×××а_nn

 

Доказательство. Последовательно разлагая определитель треугольного вида D= сначала по 1-ой строке, затем по 2-ой строке и так далее, получим

D = а₁₁×а₂₂ ×××а_nn = .

Пример 4. Вычислить определитель сведением его к треугольному виду.

D=

Решение. Чтобы свести определитель к треугольному виду, необходимо в 1-ом столбце обнулить три элемента, во 2-ом – два, в 3-ем – один и опустить их вниз, чтобы все они были под главной диагональю. Начнем обнуление с 1-го столбца. Для этой цели выберем в качестве активной 2-ую строку, у которой 1-ый элемент равен 1, а остальные элементы минимальны по модулю по сравнению с элементами 1-ой и 4-ой строк. С помощью этой активной строки обнулим 1-ый столбец.

D= = = {Вынесем общий множитель 1-ой и 2-ой строк за знак определителя и переставим местами эти строки, чтобы опустить вниз все нули в1-м столбце}= 2× = {Получилась так называемая 1-ая ступенька, которая отделяет 1-ую строку от остальных трех симметричных строк одинаково начинающихся с нулевых элементов. Это означает, что 1-ая строка больше не участвует в дальнейших преобразованиях, а мы продолжаем работать с тремя оставшимися симметричными строками. Из этих строк выбираем в качестве активной 2-ую строку, так как ее элементы минимальны по модулю, и с ее помощью обнуляем два элемента во 2-ом столбце, согласно схемы}= 2× = {Получился определитель с двумя ступеньками, которые означают, что 1-ая и 2-ая строки завершены и больше не участвуют в дальнейших преобразованиях. Мы продолжаем работать с двумя оставшимися симметричными строками, из которых выбираем в качестве активной 3-ю строку и обнуляем последний элемент в 3-ем столбце. В результате получился определитель треугольного вида, у которого все элементы ниже главной диагонали равны нулю}=

= 2× = 2∙(1∙1∙3∙(-4)) = 2×(-12) = -24

Невырожденные матрицы.

 

Обратная матрица.

Опр. Матрица называется присоединенной (союзной) к квадратной матрице А, если она состоит из алгебраических дополнений элементов транспонированной матрицы А^т. Чтобы получить присоединенную матрицу , следует транспонировать матрицу А, а затем все ее элементы заменить их алгебраическими дополнениями, то есть

= (3.1)

Опр. Квадратная матрица А называется вырожденной (особенной), если ее определитель |A|=0, и невырожденной, если ее определитель |A|¹0.

Опр. Квадратная матрица А^-1 называется обратной (инверсной) к квадратной матрице А, если выполняется условие

А^-1×А = А×А^-1= Е (3.2)

NB. Обратная матрица А^-1 возможна только для невырожденной матрицы А.

Теорема.

Для любой невырожденной квадратной матрицы А существует единственная обратная матрица А^-1, которая находится по формуле

А^-1 = (3.3)

Доказательство.

1) Из определения А^-1×А = А×А^-1 следует, что А и А^-1- это квадратные матрицы одного порядка.

Пусть матрица А – невырожденная, то есть |A|¹0. Тогда, по правилу умножения матриц, по теореме Лапласа и по свойству 9 определителей, получим

А× = × = =

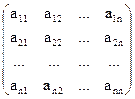= |A|× = |A|×E

Следовательно, А× = |A|×E. Аналогично доказывается, что ×А = |A|×E.

Из А× = |A|×E Þ А^-1×А× = А^-1×|A|×E Þ Е× =А^-1×|A| Þ =А^-1×|A| Þ А^-1 = .

2) Докажем единственность обратной матрицы. Предположим, что для матрицы А существует еще одна обратная матрица В. Тогда, согласно определению произведение А×В=Е. Обе части последнего равенства умножим слева на обратную матрицу А^-1 и получим: А^-1×А×В = А^-1×Е Þ Е×В = А^-1×Е Þ В = А^-1. Fin.

 

Свойства обратной матрицы:

1) |A^-1| = ;

2) (A×B)^-1 = B^-1×A^-1;

3) (A^-1)^т = (А^т)^-1.

 

3.1.1. Вычисление обратной матрицы А^-1 с помощью присоединенной матрицы .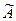

 

Для этого необходимо:

1) Вычислить определитель |A|. Если |A|=0, следовательно матрица А – вырожденная и для нее нет обратной матрицы А^-1. Если же |A|¹0, то следует выполнить следующие действия.

2) Вычислить алгебраические дополнения A_ij всех элементов a_ij матрицы А и построить матрицу А_А, в которой на местах элементов a_ij будут стоять их алгебраические дополнения A_ij:

А_А =

3) Транспонировать матрицу А_А, чтобы получить присоединенную матрицу :

= = .

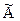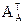4) Вычислить обратную матрицу А^-1 по формуле: А^-1 =

5) Выполнить проверку: А^-1×А = Е.

 

Пример. Дано: А= , А^-1=?

Решение: 1) Вычислим определитель |A|. Для этого сначала «обнулим» первый столбец, а затем приведем определитель к треугольному виду.

 

|A| = = = – = -(–7) = 7 ¹ 0 Þ $ А^-1.

2) Найдем алгебраические дополнения A_ij всех элементов a_ij матрицы А:

А₁₁=(-1)² = -2; А₁₂=(-1)³ = 1; А₁₃=(-1)⁴ = 0;

А₂₁=(-1)³ 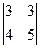= -3; А₂₂=(-1)⁴ = –16; А₂₃=(-1)⁵ = 14;

А₃₁=(-1)⁴ 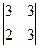= 3; А₃₂=(-1)⁵ = 9; А₃₃=(-1)⁶ = –7.

3) Составим матрицу А_А из алгебраических дополнений A_ij и транспонируем ее, чтобы получить присоединенную матрицу :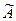

А_А= Þ = = .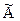

4) Найдем обратную матрицу по формуле: А^-1 = = ∙

NB. В случае, когда |A| ¹ ±1, множитель 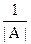лучше оставлять вне обратной матрицы А^-1 для удобства проверки.

5) Проверка: А^-1×А = ∙ ∙ = ∙ = = Е.

Ответ: А^-1 = ∙ .

3.1.2. Вычисление обратной матрицы А^-1

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: