 |
Метод Гаусса исключения неизвестных.
|
|
|
|
В отличие от матричного метода и формул Крамера метод Гаусса является универсальным, так как применим для решения и исследования на совместность не только квадратных, но любых СЛАУ. Суть метода: СЛАУ кратко записывается в виде расширенной матрицы, которая с помощью элементарных преобразований над строками приводится к ступенчатому виду. Этот процесс называется прямым ходом метода Гаусса. Тогда каждой строке ступенчатой расширенной матрицы соответствует уравнение ступенчатой СЛАУ. Ступенчатая СЛАУ несовместна, если она содержит уравнение вида 0×х1 + 0×х2 +…+0×хn = С, (где С ¹ 0), соответствующее строке  расширенной матрицы, так как такому уравнению соответствует невыполнимое равенство 0 = С. Полностью нулевые строки
расширенной матрицы, так как такому уравнению соответствует невыполнимое равенство 0 = С. Полностью нулевые строки 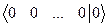 расширенной матрицы вычеркиваются, так как они соответствуют тождеству 0×х1 + 0×х2 +…+0×хn º 0, которое выполняется при любых значениях неизвестных х1, х2, …, хn.
расширенной матрицы вычеркиваются, так как они соответствуют тождеству 0×х1 + 0×х2 +…+0×хn º 0, которое выполняется при любых значениях неизвестных х1, х2, …, хn.
Решение совместной СЛАУ ступенчатого вида находят так: из последнего уравнения СЛАУ находят значение неизвестной xn и подставляют в вышестоящее уравнение, чтобы найти значение неизвестной xn-1. Далее, используя значения этих двух неизвестных, поднимаются на ступеньку выше и находят значение неизвестной xn-2 и так далее. Последним находят значение неизвестной x1 из 1-го уравнения ступенчатой СЛАУ. Описанный процесс называется обратным ходом метода Гаусса.
Пример 1. Исследовать СЛАУ на совместность и решить методом Гаусса.
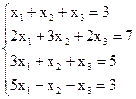
Решение. Запишем расширенную матрицу СЛАУ и элементарными преобразованиями над строками приведем ее к ступенчатому виду.











 ~
~  ~
~ 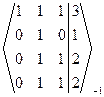 ~
~  ~
~ 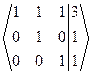 Þ Число неизвестных n = 3 = r(A) = r(A|B), то есть ранги матрицы коэффициентов и расширенной матрицы СЛАУ равны числу неизвестных. Тогда по теореме Кронекера-Капелли данная СЛАУ совместная и определенная. Полученная ступенчатая расширенная матрица СЛАУ соответствует ступенчатой СЛАУ
Þ Число неизвестных n = 3 = r(A) = r(A|B), то есть ранги матрицы коэффициентов и расширенной матрицы СЛАУ равны числу неизвестных. Тогда по теореме Кронекера-Капелли данная СЛАУ совместная и определенная. Полученная ступенчатая расширенная матрица СЛАУ соответствует ступенчатой СЛАУ
|
|
|
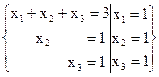
Проверка: 1+1+1=3 Û 3º3
2×1+3×1+2×1=7 Û 7º7
5×1-1-1=3 Û 3º3
Ответ: х1 = х2 = х3 = 1.
Пример 2. Исследовать СЛАУ на совместность и решить методом Гаусса.
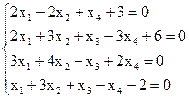
Решение. Запишем расширенную матрицу СЛАУ и элементарными преобразованиями над строками приведем ее к ступенчатому виду.


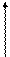





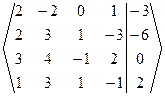 ~
~ 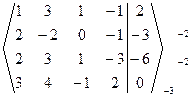 ~
~ 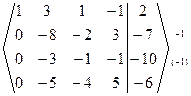 ~
~




































 ~
~ 
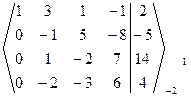 ~
~  ~
~ 



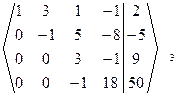 ~
~ 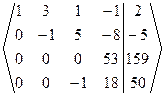 ~
~ 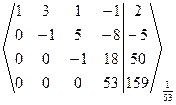 ~
~ 
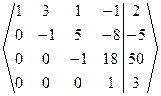 Þ Число неизвестных n=4=r(A)=r(A|B), то есть ранги матрицы коэффициентов и расширенной матрицы СЛАУ равны числу неизвестных. Тогда по теореме Кронекера-Капелли данная СЛАУ совместная и определенная. Полученная ступенчатая расширенная матрица СЛАУ соответствует ступенчатой СЛАУ
Þ Число неизвестных n=4=r(A)=r(A|B), то есть ранги матрицы коэффициентов и расширенной матрицы СЛАУ равны числу неизвестных. Тогда по теореме Кронекера-Капелли данная СЛАУ совместная и определенная. Полученная ступенчатая расширенная матрица СЛАУ соответствует ступенчатой СЛАУ 
Проверка:
2×(-2)-2×1+3+3=0 Û 0º0
2×(-2)+3×1+4-3×3+6=0 Û 0º0
3×(-2)+4×1-4+2×3=0 Û 0º0
-2+3×1+4-3-2=0 Û 0º0
Ответ: х1 = -2; х2 = 1; х3 = 4; х4 = 3.
Пример 3. Исследовать СЛАУ на совместность и решить методом Гаусса.
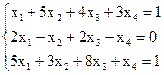
Решение. Запишем расширенную матрицу СЛАУ и элементарными преобразованиями над строками приведем ее к ступенчатому виду.




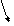

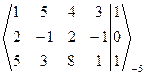 -2 ~
-2 ~ 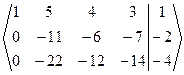 ~
~ 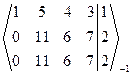 ~ ~
~ ~ 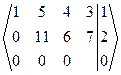 Þ Число неизвестных n=4>2=r(A)=r(A|B). По теореме Кронекера-Капелли данная СЛАУ совместная и неопределенная. Полученная ступенчатая расширенная матрица СЛАУ соответствует ступенчатой СЛАУ
Þ Число неизвестных n=4>2=r(A)=r(A|B). По теореме Кронекера-Капелли данная СЛАУ совместная и неопределенная. Полученная ступенчатая расширенная матрица СЛАУ соответствует ступенчатой СЛАУ 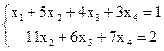
В данной ступенчатой СЛАУ число неизвестных больше числа уравнений. Поэтому она является неопределенной. Для любой неопределенной СЛАУ, когда число неизвестных превышает ранг матрицы коэффициентов (n > r(A)), часть неизвестных называют базисными (главными), а остальные – свободными неизвестными. Число базисных неизвестных равно рангу матрицы коэффициентов. В качестве базисных неизвестных берут те, коэффициенты при которых образуют базисный минор. Поскольку базисных миноров может быть несколько, то и вариантов выбора базисных неизвестных может быть несколько.
|
|
|
В данном примере за базисные неизвестные можно взять любую пару из неизвестных х1, х2, х3, х4, коэффициенты при которых образуют базисный минор. Пусть, например, это будет пара х1, х2, так как коэффициенты при этих неизвестных образуют базисный минор М2 =  = 11 ¹ 0, который берется из ступенчатой СЛАУ. Следовательно, остальные неизвестные х3, х4 являются свободными. Зафиксируем их и, чтобы отличить от базисных неизвестных, переобозначим: х3 = с3, х4 = с4. Затем перенесем их в правую часть соответствующих уравнений и выразим через них базисные неизвестные х1 и х2:
= 11 ¹ 0, который берется из ступенчатой СЛАУ. Следовательно, остальные неизвестные х3, х4 являются свободными. Зафиксируем их и, чтобы отличить от базисных неизвестных, переобозначим: х3 = с3, х4 = с4. Затем перенесем их в правую часть соответствующих уравнений и выразим через них базисные неизвестные х1 и х2:

Ответ: х1 = 1/11×(1-14с3+2с4); х2 = 1/11×(2-6с3-7с4); х3 = с3; х4 = с4, где с3, с4 - const.
Однородная СЛАУ.
В однородной СЛАУ столбец свободных членов равен нулю. Эта СЛАУ имеет вид
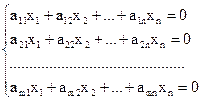 (4.8)
(4.8)
В однородной СЛАУ нулевой столбец не меняется при элементарных преобразованиях над строками расширенной матрицы. Поэтому в ней ранг матрицы коэффициентов всегда равен рангу расширенной матрицы: r(A) = r(A|B). Тогда, по теореме Кронекера-Капелли любая однородная СЛАУ всегда совместна и, согласно ее виду (4.8), всегда имеет нулевое (тривиальное) решение: х1 = … = хn = 0. Если при этом ранг матрицы коэффициентов равен числу неизвестных (r(A) = n), то для однородной СЛАУ нулевое решение является единственно возможным.
Теорема 1.
Для того, чтобы однородная СЛАУ имела ненулевые решения, необходимо и достаточно, чтобы ранг ее матрицы коэффициентов был меньше числа неизвестных (r(A) < n).
Доказательство.
1) Необходимость. Предположим обратное, то есть, что r(A) = n, где n – число неизвестных. Тогда порядок базисного минора Mn будет равен n, так как r(Mn) = r(A) = n. Следовательно, по формулам Крамера однородная СЛАУ будет иметь единственное решение – нулевое: xi = 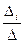 = 0, где Di = 0, а D ¹ 0. Таким образом, при r(A) = n однородная СЛАУ ненулевых решений не имеет.
= 0, где Di = 0, а D ¹ 0. Таким образом, при r(A) = n однородная СЛАУ ненулевых решений не имеет.
2) Достаточность. Пусть r(A) < n, тогда по следствию 2 теоремы Кронекера-Капелли однородная СЛАУ будет совместной и неопределенной, то есть она будет иметь бесконечное множество решений, в том числе и ненулевых. Fin.
Теорема 2.
Для того, чтобы квадратная однородная СЛАУ имела ненулевые решения, необходимо и достаточно, чтобы ее главный определитель равнялся нулю (D = 0).
|
|
|
Доказательство.
1) Необходимость. По вышеприведенной теореме 1, если однородная СЛАУ имеет ненулевые решения, то ранг ее матрицы коэффициентов должен быть меньше числа неизвестных (r(A) < n). Следовательно, главный определитель квадратной однородной СЛАУ должен быть равен нулю (D = 0).
2) Достаточность. Если главный определитель квадратной однородной СЛАУ равен нулю (D = 0), то ранг ее матрицы коэффициентов будет меньше числа неизвестных (r(A) < n). Поэтому такая СЛАУ имеет бесконечное множество ненулевых решений. Fin.
Пример. Найти ненулевые решения однородной СЛАУ.
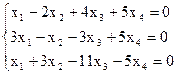
Решение. Запишем расширенную матрицу СЛАУ и элементарными преобразованиями над строками приведем ее к ступенчатому виду.





 -3 ~
-3 ~ 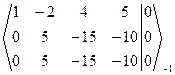 ~
~ 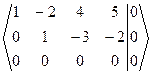 = B
= B
Число неизвестных n = 4 > 2 = r(A) = r(АВ), тогда по теореме 1 однородная СЛАУ помимо нулевого решения имеет и ненулевые решения. Найдем их. Полученной ступенчатой расширенной матрице В соответствует ступенчатая СЛАУ 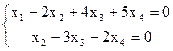
Чтобы решить ее, в качестве базисных можно взять неизвестные х1 и х2, так как коэффициенты при них образуют один из базисных миноров М2 =  = 1 ¹ 0. Следовательно, остальные неизвестные – свободные. Переобозначим их: х3 = с3, х4 = с4 и перенесем в правую часть соответствующих уравнений.
= 1 ¹ 0. Следовательно, остальные неизвестные – свободные. Переобозначим их: х3 = с3, х4 = с4 и перенесем в правую часть соответствующих уравнений.
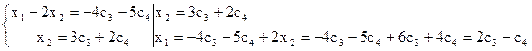
Ответ: х1 = 2с3-с4; х2 = 3с3+2с4; х3 = с3; х4 = с4, где с3, с4 - const.
Приложение 1.
Индивидуальная домашняя работа (ИДР) по теме:
«Линейная алгебра».
1) Пользуясь свойствами определителей, доказать тождество.
2) Вычислить АТ; А×АТ и ½А½.
3) Решить квадратную СЛАУ:
а) с помощью обратной матрицы;
б) по формулам Крамера.
4) Выполнить действия над матрицами.
5) Найти значения l, для которых существует обратная матрица А-1.
6) Найти ранг r(A) матрицы А.
7(а, б) Исследовать СЛАУ на совместность и решить методом Гаусса.
8) Найти ненулевые решения однородной СЛАУ.
Вариант 1.
1) 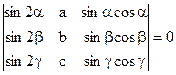
2) А = 
3) 
4) А=  ; В=
; В= 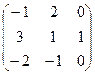 ; А2 - В-1×A=?
; А2 - В-1×A=? 
5) А= 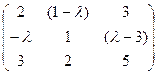
6) А=  ; r(A)=?
; r(A)=?
7(а) 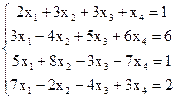
7(б) 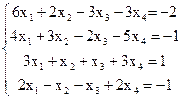
8) 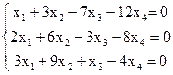
Вариант 2.
1) 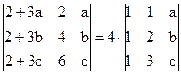
2) А = 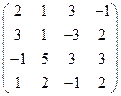
3) 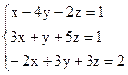
4) А=  ; В=
; В=  ; (А×B)-1 + B×A-1=?
; (А×B)-1 + B×A-1=?
5) А= 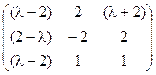
|
|
|
6) А=  ; r(A)=?
; r(A)=?
7(а) 
7(б) 
8) 
Вариант 3.
1) 
2) А = 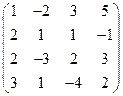
3) 
4) А=  ; В=
; В=  ; А×В-1 + 2B×A=?
; А×В-1 + 2B×A=?
5) А= 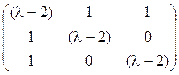
6) А= 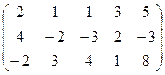 ; r(A)=?
; r(A)=?
7(а) 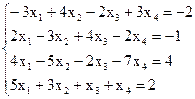
7(б) 
8) 
Вариант 4.
1) 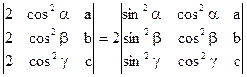
2) А = 
3) 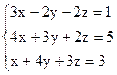
4) А=  ; В=
; В= 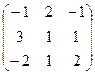 ; А-1×B - A×B-1=?
; А-1×B - A×B-1=?
5) А= 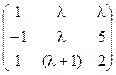
6) А= 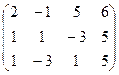 ; r(A)=?
; r(A)=?
7(а) 
7(б) 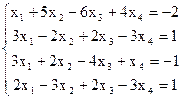
8) 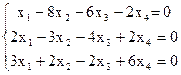
Вариант 5.
1) 
2) А = 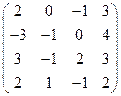
3) 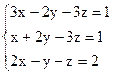
4) А=  ; В=
; В=  ; А2 - В-1×A=?
; А2 - В-1×A=?
5) А= 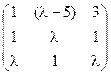
6) А= 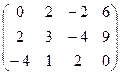 ; r(A)=?
; r(A)=?
7(а) 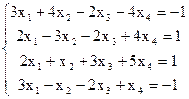
7(б) 
8) 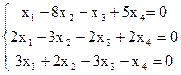
Вариант 6.
1) 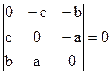
2) А = 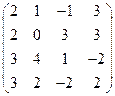
3) 
4) А=  ; В=
; В=  ; А2 - В×A-1=?
; А2 - В×A-1=?
5) А= 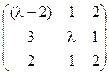
6) А= 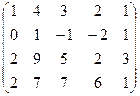 ; r(A)=?
; r(A)=?
7(а) 
7(б) 
8) 
Вариант 7.
1)  =2
=2 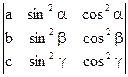
2) А = 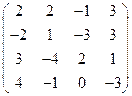
3) 
4) А=  ; В=
; В=  ; А×B-1 + В×A=?
; А×B-1 + В×A=?
5) А= 
6) А= 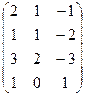 ; r(A)=?
; r(A)=?
7(а) 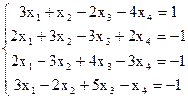
7(б) 
8) 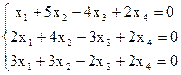
Вариант 8.
1) 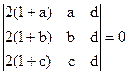
2) А = 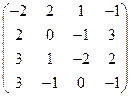
3) 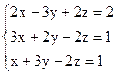
4) А=  ; В=
; В=  ; B×A-1 - A×B-1=?
; B×A-1 - A×B-1=?
5) А= 
6) А= 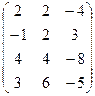 ; r(A)=?
; r(A)=?
7(а) 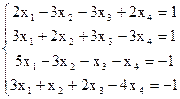
7(б) 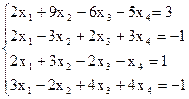
8) 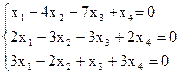
Вариант 9.
1) 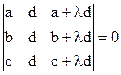
2) А = 
3) 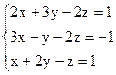
4) А=  ; В=
; В=  ; 2(А×B)-1 - A×В =?
; 2(А×B)-1 - A×В =?
5) А= 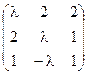
6) А= 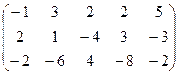 ; r(A)=?
; r(A)=?
7(а) 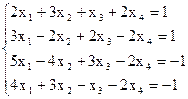
7(б) 
8) 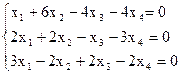
Вариант 10.
1) 
2) А = 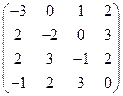
3) 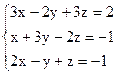
4) А=  ; В=
; В=  ; 2В-1×A + B×A=?
; 2В-1×A + B×A=?
5) А= 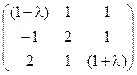
6) А= 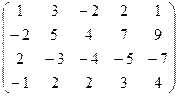 ; r(A)=?
; r(A)=?
7(а) 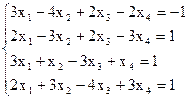
7(б) 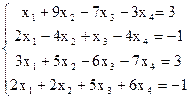
8) 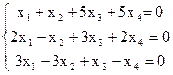
Вариант 11.
1)  =0
=0
2) А = 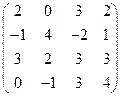
3) 
4) А=  ; В=
; В=  ; 2(B×А)-1 + В×A=?
; 2(B×А)-1 + В×A=?
5) А= 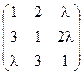
6) А= 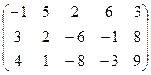 ; r(A)=?
; r(A)=?
7(а) 
7(б) 
8) 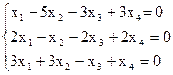
Вариант 12.
1) 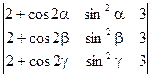 =0
=0
2) А = 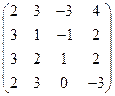
3) 
4) А=  ; В=
; В=  ; А×B-1 + 2(B×A)-1=?
; А×B-1 + 2(B×A)-1=?
5) А= 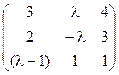
6) А= 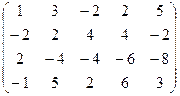 ; r(A)=?
; r(A)=?
7(а) 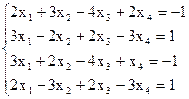
7(б) 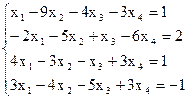
8) 
Вариант 13.
1) 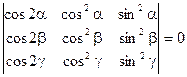
2) А = 
3) 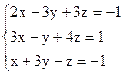
4) А=  ; В=
; В=  ; B-1×А + В×А-1=?
; B-1×А + В×А-1=?
5) А= 
6) А= 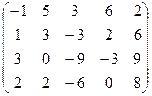 ; r(A)=?
; r(A)=?
7(а) 
7(б) 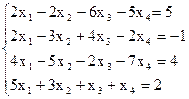
8) 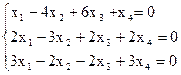
Вариант 14.
1) 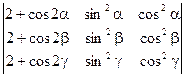 =0
=0
2) А = 
3) 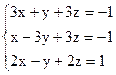
4) А=  ; В=
; В=  ; В×A-1 + B×А=?
; В×A-1 + B×А=?
5) А= 
6) А=  ; r(A)=?
; r(A)=?
7(а) 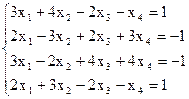
7(б) 
8) 
Вариант 15.
1) 
2) А = 
3) 
4) А=  ; В=
; В=  ; А-1×B + В-1×А=?
; А-1×B + В-1×А=?
5) А= 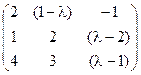
6) А= 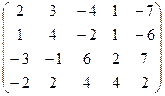 ; r(A)=?
; r(A)=?
7(а) 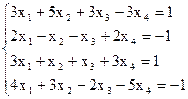
7(б) 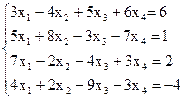
8) 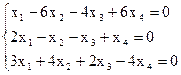
Вариант 16.
1) 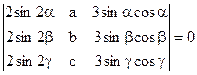
2) А = 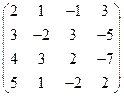
3) 
4) А=  ; В=
; В= 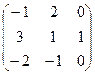 ; А×В - В-1×А-1=?
; А×В - В-1×А-1=? 
5) А= 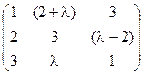
6) А=  ; r(A)=?
; r(A)=?
7(а) 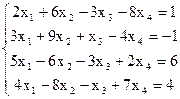
7(б) 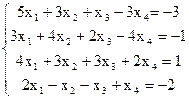
8) 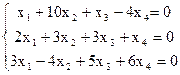
Вариант 17.
1) 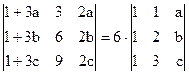
2) А = 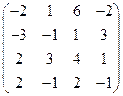
3) 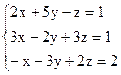
4) А=  ; В=
; В=  ; (B×A)-1 + A×B-1=?
; (B×A)-1 + A×B-1=?
5) А= 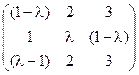
6) А= 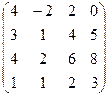 ; r(A)=?
; r(A)=?
7(а) 
7(б) 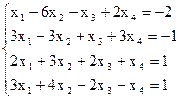
8) 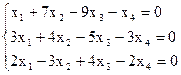
Вариант 18.
1) 
2) А = 
3) 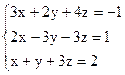
4) А=  ; В=
; В=  ; В-1×A + 2A×B=?
; В-1×A + 2A×B=?
5) А= 
6) А=  ; r(A)=?
; r(A)=?
7(а) 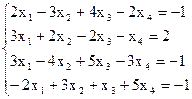
7(б) 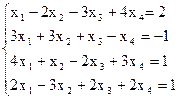
8) 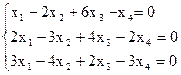
Вариант 19.
1) 
2) А = 
3) 
4) А=  ; В=
; В= 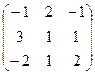 ; A-1×B + B×A=?
; A-1×B + B×A=?
5) А= 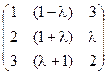
6) А= 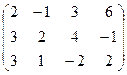 ; r(A)=?
; r(A)=?
7(а) 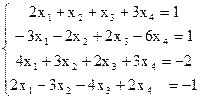
7(б) 
8) 
Вариант 20.
1) 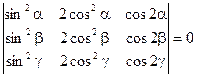
2) А = 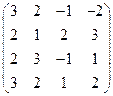
3) 
4) А=  ; В=
; В=  ; (А×В)-1 + A×B=?
; (А×В)-1 + A×B=?
5) А= 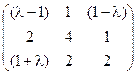
6) А= 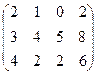 ; r(A)=?
; r(A)=?
7(а) 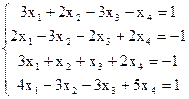
7(б) 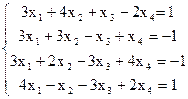
8) 
Вариант 21.
1) 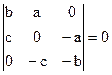
2) А = 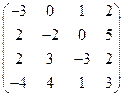
3) 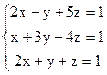
4) А=  ; В=
; В=  ; B×А-1 - В×A=?
; B×А-1 - В×A=?
5) А= 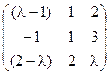
6) А= 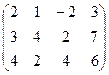 ; r(A)=?
; r(A)=?
7(а) 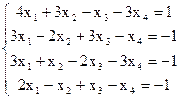
7(б) 
8) 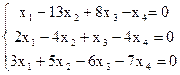
Вариант 22.
1)  =
= 
2) А = 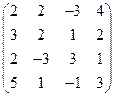
3) 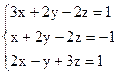
4) А=  ; В=
; В=  ; А×B-1 + (A×B)-1=?
; А×B-1 + (A×B)-1=?
5) А= 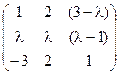
6) А= 
 ; r(A)=?
; r(A)=?
7(а) 
7(б) 
8) 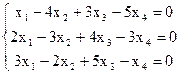
Вариант 23.
1) 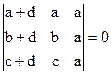
2) А = 
3) 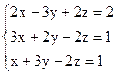
4) А=  ; В=
; В=  ; B×A-1 - A×B-1=?
; B×A-1 - A×B-1=?
5) А= 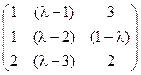
6) А=  ; r(A)=?
; r(A)=?
7(а) 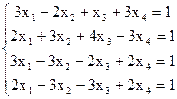
7(б) 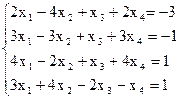
8) 
Вариант 24.
1) 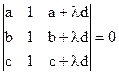
2) А = 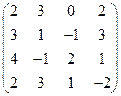
3) 
4) А=  ; В=
; В=  ; 2А×B-1 + A-1×В =?
; 2А×B-1 + A-1×В =?
5) А= 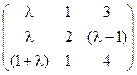
6) А= 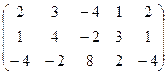 ; r(A)=?
; r(A)=?
7(а) 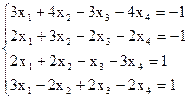
7(б) 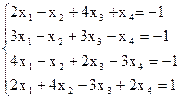
8) 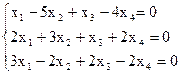
Вариант 25.
1) 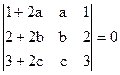
2) А = 
3) 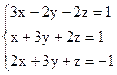
4) А=  ; В=
; В=  ; 2В-1×A + B×A-1=?
; 2В-1×A + B×A-1=?
5) А= 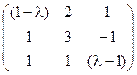
6) А= 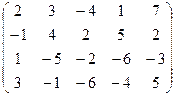 ; r(A)=?
; r(A)=?
7(а) 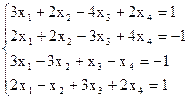
7(б) 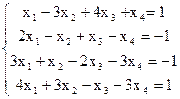
8) 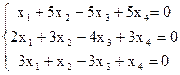
Вариант 26.
1) 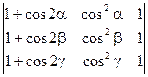 =0
=0
2) А = 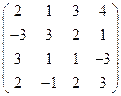
3) 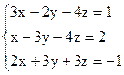
4) А=  ; В=
; В=  ; (B×А)-1 - 2A×В=?
; (B×А)-1 - 2A×В=?
5) А= 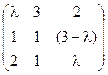
6) А= 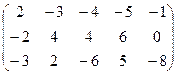 ; r(A)=?
; r(A)=?
7(а) 
7(б) 
8) 
Вариант 27.
1) 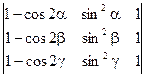 =0
=0
2) А = 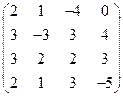
3) 
4) А=  ; В=
; В=  ; B-1×A + (A×B)-1=?
; B-1×A + (A×B)-1=?
5) А= 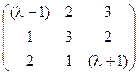
6) А= 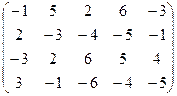 ; r(A)=?
; r(A)=?
7(а) 
7(б) 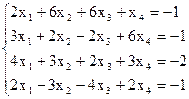
8) 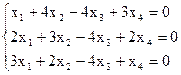
Вариант 28.
1) 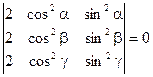
2) А = 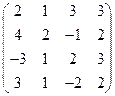
3) 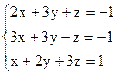
4) А=  ; В=
; В=  ; А-1×B + A×В-1=?
; А-1×B + A×В-1=?
5) А= 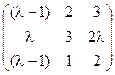
6) А= 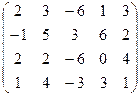 ; r(A)=?
; r(A)=?
7(а) 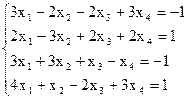
7(б) 
8) 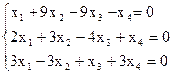
Вариант 29.
|
|
|
1) 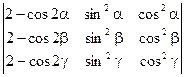 =0
=0
2) А = 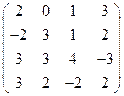
3) 
4) А= 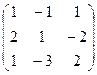 ; В=
; В=  ; B-1×A - (B×A)-1=?
; B-1×A - (B×A)-1=?
5) А= 
6) А=  ; r(A)=?
; r(A)=?
7(а) 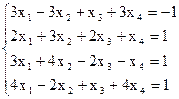
7(б) 
8) 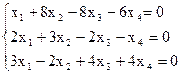
Вариант 30.
1) 
2) А = 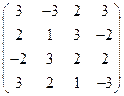
3) 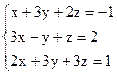
4) А=  ; В=
; В=  ; (B×A)-1 - B×A-1=?
; (B×A)-1 - B×A-1=?
5) А= 
6) А=  ; r(A)=?
; r(A)=?
7(а) 
7(б) 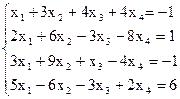
8) 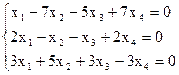
Приложение 2.
|
|
|


