 |
Геометрия диффузионной среды
|
|
|
|
Лекция 3. ОСНОВНЫЕ ЗАКОНЫ ДИФФУЗИИ
Математика законов Фика
Рассмотрим теперь диффузионные уравнения, связанные с законами Фика более подробно.
Однородная изотропная среда
В случае трехмерной диффузии первый закон Фика имеет вид:
⎛ ∂ ∂ ∂ ⎞
j = − D ⎜ C +
C + C ⎟ = − D grad C = − D ∇ C, (1)
∂ z ⎠
где j – поток диффузанта через единицу поверхности.
Второй закон Фика:
= D ⎜
C + ∂
C + = ∂
2 ⎞
|
|
∂ y 2
∂ z 2 ⎟
В простейшем случае одномерной диффузии (например, диффузии в неограниченной пластине) двумя основными дифференциальными формами законов диффузии Фика являются:
∂ C (x)
|
и
∂ C (x, t)
= D
∂ t
∂ x
∂2 C (x, t)
∂ x 2
(1а)
(2а)
Ур.1а дает скорость проникновения диффузанта через единицу поверхности некоторой среды при стационарном состоянии потока, выраженную через градиент концентрации и постоянную, называемую коэффициентом диффузии D. S- площадь поверхности, через которую проходит диффузионный поток. Второе уравнение определяет накопление диффузанта в определенной точке среды как функцию времени. Таким образом, это уравнение относится к нестационарному состоянию потока.
Неоднородная среда
В неоднородной среде, коэффициент диффузии является функцией координаты, тогда:
D = f (x, y, z) и
∂ ∂ ⎛ ∂ ⎞
∂ ⎛ ∂ ⎞
∂ ⎛ ∂ ⎞
C = ⎜ D
∂ t ∂ x ⎝
C
⎟ +
∂ x ⎠
⎜ D
∂ y ⎝
C ⎟ +
∂ y ⎠
⎜ D
∂ z ⎝
⎟ = div (D grad C). (3)
|
В анизотропной среде, диффузия идет по каждой из координатной оси со своим
|
|
|
коэффициентом диффузии
Имеем:
Dx, D y и
Dz.
∂ C
∂ t = Dx
∂2 C
∂ x 2
+ D y
∂2 C
∂ y 2
+ Dz
∂2 C
∂ z 2
. (4)
Если воспользоваться подстановкой обычную форму диффузионного уравнения:
ξ = x D;
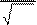Dx
η = y D;
D y
ς = z
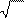
D, то получим
Dz
∂ C ⎛ ∂ 2 C
= D ⎜
∂2 C
+
∂ 2 C ⎞
|
|
∂η2
∂ς ⎠
Необходимо учитывать, что при осложнении диффузии другими параллельно идущими процессами ход этого комплексного процесса должен описываться выражениями, отличными от вытекающих из решений «классических» уравнений диффузии. Предположение о постоянстве D
оправдывается не всегда – часто коэффициент диффузии зависит от концентрации диффузанта, градиента концентрации, пространственной координаты и времени диффузионного эксперимента (а иногда – от всех этих параметров вместе). Несложно осуществить вывод уравнений диффузии, когда D не является постоянным. Уравнение первого закона Фика при этом остается неизменным, а при выводе уравнения второго закона D, как переменную величину не выносят за знак повторного дифференцирования.
1.2 Концентрационная зависимость коэффициента диффузии.
Если коэффициент диффузии является функцией концентрации
многомерном случае
D = f (C), то в
∂ ∂ ⎡ ∂ ⎤
∂ ⎡ ∂ ⎤
C = D C +
C = ∂ ⎡ = ∂ C ⎤
|
∂ t ∂ x
∂ x ∂ y ⎣
∂ y ⎦ ∂ z ∂ z
В случае одномерной диффузии:
∂ C ∂ C ⎛
∂ C ⎞
∂2 C
∂ D (C)
⎛ ∂ C ⎞
= ⎜ D
⎟ = D (C) +
⋅⎜ ⎟
. (7)
∂ t ∂ x ⎝
∂ x ⎠
∂ x 2
∂ C ⎝ ∂ x ⎠
|
A (C) = ∂ D (Ci);
B (C)= D (C), тогда Ур.7 перепишется в виде:
∂ Ci
∂
i i
⎛ ∂ ⎞ 2
|
Ci ⎟
|
|
|
+ B (C) ∂ Ci
(7а)
∂ t ⎝ ∂ x ⎠
i ∂ x 2
Временная зависимость коэффициента диффузии
Если коэффициент диффузии зависит от времени
D = f (τ), то можно воспользоваться
решениями уравнений для постоянного коэффициента диффузии, используя подстановку:
|
t
Геометрия диффузионной среды
|
Рис.1 Деление диффузионного тока на элементарные объемы
Предположим, что площадь поперечного сечения тела, перпендикулярного диффузионному потоку S, переменна. Разобьем тело на ряд элементарных объемов длиной dr и введем понятие трубки тока.
Диффузия по такой трубке тока будет описываться общим дифференциальным уравнением:
∂ C = 1
∂ ⎛
⎜ DS
∂ C ⎞
⎟, (9)
∂ t S ∂ r ⎝
∂ r ⎠
где r – некоторое произвольное направление (оно может быть и изогнутым).
3
Легко видеть, что уравнение (9) рассматривает декартовы координаты как частный случай математического описания твердого тела, которое приводит к системе трех прямолинейных ортогональных диффузионных линий. В общем случае на практике гораздо удобнее не пользоваться произвольной системой координат, а разделить твердое тело сетью линий тока в соответствии с их реальным расположением в теле. Особенно такой подход перспективен при изучении диффузии в сложных средах.
Из уравнения (9) легко получить выражения для одномерных задач, когда поверхность S
является однозначной функцией координаты r, т.е. S (r), или является величиной постоянной.
Например, полагая
S (r) = 4π r 2, мы получим дифференциальное уравнение диффузии для шара:
1) Сферические координаты
Трехмерное уравнение диффузии может быть выражено в сферических координатах r, θ и φ при помощи уравнений преобразования: x=rsinθcosφ, y=rsinθsinφ, z=rcosφ
Тогда уравнение для 2-го закона Фика принимает вид:
C D ⎛
C ⎞ 1 ⎛
C ⎞ 1 2 C
∂ ⎡ ∂ 2 ∂
= 2 ⎢ ⎜ r ⎟ +
∂ ⎜sinθ ∂ ⎟ +
∂ ⎤
2 2 ⎥
(10)
|
|
|
∂ t r
⎣∂ r ⎝
∂ r ⎠
sinθ ∂θ ⎝
∂θ ⎠
sin
θ ∂ϕ ⎦
Если коэффициент диффузии нельзя считать постоянным, то
∂ C 1 ⎡ ∂ ⎛
2 ∂ C ⎞
1 ∂ ⎛
∂ C ⎞
1 ∂ ⎛
∂ C ⎞⎤
= 2 ⎢
⎜ Dr ⎟ +
⎜ D sinθ
⎟ + 2
⎜ D ⎟⎥
(11)
∂ t r
⎣∂ r ⎝
∂ r ⎠
sinθ ∂θ ⎝
∂θ ⎠
sin
θ ∂ϕ ⎝
∂ϕ ⎠⎦
2) В случае сферически симметричной диффузии (диффузия в шаре):
∂ C = = 1 ⎡ = ∂ ⎛ Dr 2 = ∂ C ⎞⎤, (12)
2 ⎢ ⎜ ⎟⎥
при D=const имеем
∂ t r
⎣∂ r ⎝
∂ r ⎠⎦
∂ C ⎛ ∂2 C
= D ⎜
2 ∂ C ⎞
|
|
r ∂ r ⎟
Если положить
S (r) = 2π rh, где h – высота цилиндра (h = const), получим уравнение
диффузии для неограниченного цилиндра (h >> R, где R – радиус цилиндра).
3) Диффузия в образце цилиндрической формы.
В цилиндрической системе координат координатами являются радиус r, угол θ и расстояние вдоль оси цилиндра z. Связь цилиндрических координат с декартовыми выражается соотношениями: x=rcosθ, y=rsinθ. В этом случае выражение для 2-го закона Фика принимает вид:
∂ C = = 1 ⎡ = ∂ ⎛ Dr = ∂ C ⎞ + = ∂
⎛ = D ∂ C ⎞ + = ∂ ⎛ Dr = ∂ C ⎞⎤
⎢ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟⎥
(14)
∂ t r ⎣∂ r ⎝
∂ r ⎠
∂θ ⎝ r
∂θ ⎠
∂ z ⎝
∂ z ⎠⎦
При постоянном коэффициенте диффузии:
∂ C = = D ⎡ = ∂ ⎛ r = ∂ C ⎞ + = ∂
⎛ = 1 ∂ C ⎞ + = ∂ ⎛ r = ∂ C ⎞⎤
⎢ ⎜ ⎟
⎜ ⎟ ⎜ ⎟⎥
(15)
∂ t r ⎣∂ r ⎝
∂ r ⎠
∂θ ⎝ r ∂θ ⎠
∂ z ⎝
∂ z ⎠⎦
4) Неограниченный цилиндр:
Если распределение концентрации зависит только от радиуса r и не зависит от координат θ и z, будет иметь место случай цилиндрической (аксиальной) симметрии; диффузия в этом случае подчиняется уравнению:
∂ C = = 1 ⎡ = ∂ ⎛ Dr = ∂ C ⎞⎤
⎢ ⎜ ⎟⎥
(16)
∂ t r ⎣∂ r ⎝
∂ r ⎠⎦
|
|
|
|
∂ C ⎛ ∂2 C
= D ⎜
1 ∂ C ⎞
+ ⎟. (17)
|
r ∂ r ⎟
5) Конечный цилиндр:
∂ C ⎛ ∂2 C
= D ⎜
+ 1 ∂ C + 1
∂ 2 C
∂2 C ⎞
|
|
r ∂ r
r 2 ∂θ 2
∂ z 2 ⎟
где θ – азимутальный угол, z – направление оси цилиндра.
6) Пластина:
j = − D ∂ C;
∂ x
∂ C = D
∂ t
∂2 C
∂ x 2
. (19)
В общем случае дифференциальное уравнение диффузии при постоянном коэффициенте
∂ C (ξ1, ξ2, ξ3) 2
1 ∑ ∂
α1α2α3 ∂ C (ξ1, ξ2, ξ3)
t
C (ξ1,ξ2,ξ3) = D ⎨αα α ξ 2
ξ ⎬, (20)
∂
3 ⎛ ∂ x ⎞
1 2 3 i =1 ∂ α i ∂ i
|
j =1 ⎝ ∂ξ i ⎠
j = 1,2,3;
x j – декартовы координаты.
виде:
Часто дифференциальное уравнение диффузии в среде произвольной формы записывают в
∂ C = D = 1
⎡ = ∂ ⎛ r ν = ∂ C ⎞⎤, (21)
ν ⎢ ⎜ ⎟⎥
∂ t r
⎣∂ r ⎝
∂ r ⎠⎦
где параметр ν определяет геометрию образца.
В частном случае
ν=0, -R≤ r≤R – цилиндр с непроницаемой боковой поверхностью (таблетка, пластина);
ν=1, 0≤ r≤R – цилиндр с непроницаемыми торцами;
ν=1, R1≤ r≤R2 – полый цилиндр непроницаемыми торцами;
ν=2, 0≤ r≤R – сфера (шар);
ν=2, R1≤ r≤R2 – полая сфера (сферическая оболочка).
|
|
|
