I. Соотношение риска и доходности для портфеля из двух активов при различных коэффициентах корреляции.

Доходность портфеля (r) из т ценных бумаг есть средневзвешенная доходность по включаемым ценным бумагам:

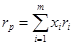, где х — доля инвестирования в данную ценную бумагу i.

Риск портфеля из т ценных бумаг зависит от:

1) риска отдельных ценных бумаг, включенных в него (s_i, где i — ценная бумага в портфеле, i = 1,..., т);

2) корреляции ценных бумаг (синхронности изменения доходности);

3) доли инвестирования в каждую ценную бумагу X_i, , где I — денежные средства, инвестированные в портфель; I_i — денежные средства,инвестированные в ценную бумагу i, .

Для оценки тесноты связи используются два показателя:

- ковариация (cov_ij);

- коэффициент корреляции (r_ij).

Коэффициент корреляции более удобен для сравнения различных активов. Его значения находятся в интервале от —1 до +1.

Для п наблюдений изменения доходности по двум активам ковариация рассчитывается следующим образом:

cov_ij = r_ijs_is_j.

Для абсолютно независимых активов коэффициент корреляции равен -1.

Если r_ij = + 1, то дисперсия портфеля равна

Наилучший результат диверсификации достигается, если два актива отрицательно коррелируют. На практике это наблю­дается крайне редко, однако для примера предположим, что r_ij = —1. В этом случае дисперсия портфеля равна нулю. Для такого случая портфельная страте­гия в установлении весов Х_i и Х_j будет строиться на выполнении соотношения

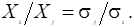
При нулевой корреляции портфельный риск 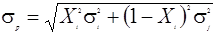,а в общем случае формирования портфеля из двух активов:

 

 

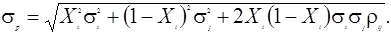
Анализ соотношения риска и доходности портфеля

Пусть рассматриваются два варианта инвестирования (в активы Z и Y), харак­теристики ожидаемой доходности, риска и корреляции по которым известны и показаны в таблице 6 (слайд 17).

Таблица 6. Характеристики двух вариантов инвестирования.

Активы	Ожидаемая доходность, %	Стандартное отклонение, %	Коэффициент корреляции
Z Y			rZY = — 0,25

Активы Z и Y могут комбинироваться в любой пропорции, т.е. абсолютно делимы (отметим, что только инвестирование в ценные бумаги почти удовлетворяет этому свойству). Следовательно, существует неограниченное число возможных комбинаций риска и доходности. Все комбинации показаны на рисунке 10 (слайд 18).

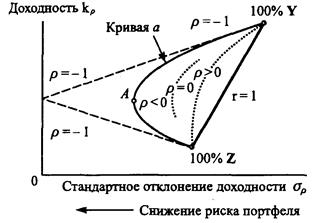
Рисунок 10. Соотношение риска и доходности для портфеля из двух активов при различных коэффициентах корреляция и весовых коэффициентов.

Ставя цель минимизации риска, следует инвестировать только в актив Z, так как он обеспечивает наименьшее значение стандартного отклонения. Однако такой выбор ошибочен с точки зрения соотношения риска и доход­ности. Поскольку Z и Y отрицательно коррелируют, такая же доходность, как и по активу Z, может быть достигнута с меньшим риском. При переходе от портфеля "100% Z" к "75% Z + 25%Y" риск снижается и растет ожидаемая доходность. Однако этот эффект не бесконечен. Чем больше доля Y, тем эффект большего риска Y перевешивает выгоды отрицательной корреляции в комбина­ции активов Z и Y и, как результат, общий риск растет. Рис. 10 показывает множество возможных вариантов комбинации активов. Точка Y показывает вариант 100%-го инвестирования в активы Y, точка Z — 100%-е инвестирование в Z, точка А — вариант инвестирования с наименьшим риском (портфель А = 75% Z + 25%Y).

Изменение коэффициента корреляции р приведет к иным соотношениям риска и доходности в портфелях из активовY и Z, что показано на рис. 10.

При принятии решений инвестор имеет определенные возможности (в зависимости от инвестируемых де­нежных средств и цены покупки каждого актива) формирования портфеля рисковых активов.

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: