 |
Математическое ожидание случайной величины
|
|
|
|
37.1. Функция распределения вероятностей или плотность вероятности являются полными вероятностными характеристиками случайной величины. Однако, во многих задачах такая полная характеристика случайной величины, с одной стороны, может быть неизвестна для исследователя, а с другой стороны и не обязательна, достаточно ограничиться значением некоторых параметров распределения вероятностей, т.е. некоторых чисел (или числовых характеристик). Здесь уместна аналогия с геометрическим описанием сложной формы твердого тела, когда ограничиваются такими характеристиками (числами) как длина, ширина, высота, объем, момент инерции, и т.д., а детальное описание сложной формы этого тела не рассматривается. Числовыми характеристиками случайных величин чаще всего служат так называемые моменты распределения, простейшим из которых является математическое ожидание случайной величины.
Прежде чем вводить определение математического ожидания случайной величины, рассмотрим выражение среднего арифметического результатов измерения дискретной случайной величины. Пусть случайная величина 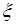 может принимать значения
может принимать значения  соответственно с вероятностями
соответственно с вероятностями  . Результат измерения случайной величины
. Результат измерения случайной величины 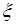 в каждом опыте - это одно из чисел
в каждом опыте - это одно из чисел  . Пусть выполнено
. Пусть выполнено  опытов, среди них в
опытов, среди них в 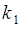 опытах случайная величина
опытах случайная величина 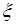 принимала значение
принимала значение  , в
, в 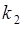 опытах - значение
опытах - значение  ,..., в
,..., в 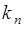 опытах - значение
опытах - значение  . Очевидно,
. Очевидно,  - полное число опытов. Пусть
- полное число опытов. Пусть  - среднее арифметическое результатов измерения случайной величины
- среднее арифметическое результатов измерения случайной величины 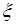 в
в  опытах, тогда
опытах, тогда
 , (37.1)
, (37.1)
где 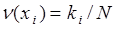 - частота появления числа
- частота появления числа  при измерении случайной величины
при измерении случайной величины 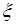 в
в  опытах. С увеличением числа опытов
опытах. С увеличением числа опытов  величина
величина  приближается к числу
приближается к числу 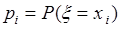 . Поэтому для того, чтобы определить теоретический аналог среднего арифметического
. Поэтому для того, чтобы определить теоретический аналог среднего арифметического  достаточно в формуле (37.1) частоту
достаточно в формуле (37.1) частоту  заменить на вероятность
заменить на вероятность 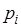 . Это приводит к следующему определению.
. Это приводит к следующему определению.
|
|
|
Математическим ожиданием (средним, статистическим средним) дискретной случайной величины 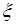 , принимающей значения
, принимающей значения  с вероятностями
с вероятностями  , называется число
, называется число
 . (37.2)
. (37.2)
Если множество значений дискретной случайной величины счетно:  , то в (37.2) полагается
, то в (37.2) полагается 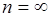 .
.
Пусть 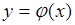 - однозначная функция одной переменной,
- однозначная функция одной переменной, 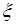 - дискретная случайная величина, принимающая значения
- дискретная случайная величина, принимающая значения  с вероятностями
с вероятностями  . Тогда
. Тогда  - дискретная случайная величина, принимающая значения
- дискретная случайная величина, принимающая значения  с вероятностями
с вероятностями  . Поэтому из определения (37.2) математического ожидания следует
. Поэтому из определения (37.2) математического ожидания следует
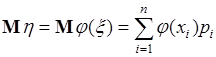 (37.3)
(37.3)
- выражение, определяющее математическое ожидание функции  .
.
Математическим ожиданием непрерывной случайной величины 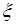 с плотностью распределения вероятностей
с плотностью распределения вероятностей 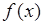 называется число
называется число
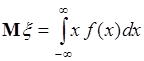 . (37.4)
. (37.4)
Аналогично определяется математическое ожидание случайной величины  - как число
- как число
 , (37.5)
, (37.5)
где  - однозначная функция одной переменной,
- однозначная функция одной переменной,  - плотность распределения вероятностей случайной величины
- плотность распределения вероятностей случайной величины 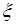 .
.
37.2. Определения (37.2) и (37.4) согласуются друг с другом. Соотношение (37.4) можно представить приближенно в виде интегральной суммы:
 , (37.6)
, (37.6)
где 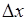 - малая величина. Тогда
- малая величина. Тогда 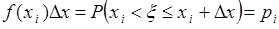 , и следовательно, (37.4) формально представимо суммой (37.2).
, и следовательно, (37.4) формально представимо суммой (37.2).
Если  - дискретная величина, принимающая значения
- дискретная величина, принимающая значения  с вероятностями
с вероятностями  , то ее плотность вероятности
, то ее плотность вероятности 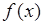 можно представить через
можно представить через 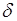 - функцию:
- функцию:
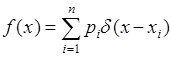 . (37.7)
. (37.7)
Подставим (37.7) в (37.4), тогда
 , (37.8)
, (37.8)
что совпадает с (37.2). Таким образом, определение (37.4) математического ожидания можно использовать как универсальное определение как для непрерывных, так и для дискретных случайных величин. Однако вычислять математическое ожидание дискретной случайной величины, конечно, удобнее по формуле (37.2).
|
|
|
Выражение (37.4) можно представить через функцию распределения  случайной величины
случайной величины  . Для этого выполним следующие преобразования:
. Для этого выполним следующие преобразования:  . Далее используем для вычисления интеграла способ «по частям»:
. Далее используем для вычисления интеграла способ «по частям»:
 .
.
Пусть функция  удовлетворяет условиям:
удовлетворяет условиям:  ,
,  , тогда
, тогда
 . (37.9)
. (37.9)
Это выражение позволяет вычислять математическое ожидание  через функцию распределения
через функцию распределения 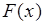 .
.
|
|
|


